What is a buffering circuit?

Op-amps have a variety of uses. One use is as a so-called buffer. A buffer is something that isolates or separates one circuit from another. In order to explain this more precisely, let's take a closer look at our 3-bit DAC.

The 3-bit DAC constructed in the previous lab produced a digitally controlled voltage, but it turns out that we can't really use this voltage as a source to drive other circuits. The problem is that if we were to attach another circuit to our DAC, then we would be changing the $R2R$ ladder network and hence would change the voltage produced by that network. We refer to this phenomenon as loading. The problem with our circuit is that it produces a voltage that is not insensitive to the load on the circuit.

We now use our preceding discussion about Thevenin circuits to study the loading problem. Our preceding discussion asserted that a simpler circuit known as the Thevenin equivalent can always produce the output voltage of any resistive network with independent sources. Figure 4 shows the original DAC network (assuming only one of the output pins is high) and its associated Thevenin equivalent.

Figure 4: Thevenin equivalent of the DAC network

Assuming that the Thevenin equivalent voltage $V_{\rm eq}$ and resistance $R_{\rm eq}$ are known, then we can go ahead an determine the effect that a load resistance has on the circuit's output voltage by a simple application of the voltage divider law. If we place a load with resistance $R_{\rm load}$ between the DAC's output node and ground, then the loaded Thevenin equivalent circuit would be as shown in figure 5 and the resulting output voltage would be

$$V_{\rm out} = \frac{R_{\rm load}}{R_{\rm eq} + R_{\rm load}} V_{\rm eq}$$ (1)

Figure 5: Loaded Thevenin equivalent circuit

Remember that $V_{\rm eq}$ is the open circuit voltage generated by the circuit and this is precisely the voltage that we wanted our DAC to generate. Since the resistances $R_{\rm eq}$ and $R_{\rm load}$ are positive, this means that the ratio. $R_{\rm load}/(R_{\rm load}+R_{\rm eq})$ must be less than one. In other words, the output voltage of the loaded DAC will always be less than what we want it to be.

As a numerical example, let's assume that $R_{\rm eq}$ is 1 k-ohm and let's assume that $R_{\rm load}$ equals 8 ohms. This rather low load resistance is common for some devices such as audio speakers. The ratio is now readily seen to be

$$V_{\rm out}=\frac{R_{\rm load}}{R_{\rm eq}+R_{\rm load}}V_{\rm eq} = \frac{8}{1000+8} V_{\rm eq} \approx 0.008 V_{\rm eq}$$

In other words, the output voltage is dramatically less than what we wanted our DAC to produce.

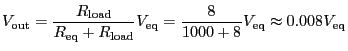The bottom line in our preceding discussion is that connecting a load to a circuit always effects the output voltage that the circuit will generate. We can minimize the sensitivity of the output voltage to the load resistance by designing the circuit so its Thevenin equivalent resistance, $R_{\rm eq}$, is large. From equation 1, we see that the ratio $R_{\rm load}/(R_{\rm load}+R{\rm eq})$ can be made arbitrarily small by selecting $R_{\rm eq}$ arbitrarily large.

In order for our DAC to be useful, we'll need to find a way of redesigning the DAC, so that its Thevenin equivalent output resistance is very large. If this is done, then the output voltage generated by the DAC will be insensitive to variations in the load resistance. We can accomplish this feat by simply augmenting our existing ladder network with a buffering amplifier.

A buffer is a unity-gain amplifier that has an extremely high input resistance and an extremely low output resistance. This means that the buffer can be modelled as a voltage controlled voltage source that has a gain of one. We connect the buffer to our DAC as shown in figure 6. Note that we've represented the DAC by its Thevenin equivalent circuit. Since the buffer has an infinite input resistance, there is no loading effect so that $V_{\rm in} = V_{\rm eq}$. Moreover, we know that the output voltage produced by the buffer must be equal to $V_{\rm in}$ since it has a gain of 1. In other words the voltage produced by the buffer is precisely the voltage generated by the DAC. The output voltage from the buffer is insensitive to the load resistance because the idealized buffer has an output resistance that is essentially zero. By placing a unity gain buffer between the DAC and the load, we have, therefore, solved our loading problem.

Figure 6: Circuit diagram for DAC buffered by unity gain amplifier

Unity gain buffers are idealized circuit elements. While it is possible to buy integrated circuits that serve as these idealized buffers, it is easy to build your own buffer from an operational amplifier. Recall that the op-amp has a large gain, near infinite input resistance and near zero output resistance. In order to turn it into a unity gain buffer, all we need to do is find a way of reducing the overall gain of the op-amp to unity. This can be done using the non-inverting op-amp circuit shown in figure 7. You will be asked to analyze this circuit as part of the pre-lab.

Figure 7: Non-inverting op-amp connection