What is an Alternating Voltage?

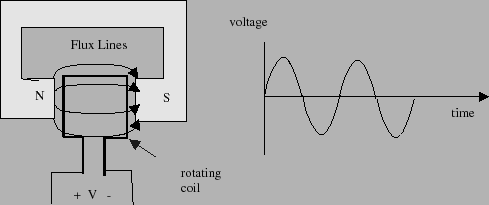
Faraday's law of induction provides a basis for converting mechanical energy into electrical energy. The basic idea is to move a coil of wire relative to a magnetic field. This motion will generate a current in the wire. Such a device is called a generator and a conceptual drawing of this device is shown in figure 1.

Figure 1: A generator and the voltage it generates

To make things simple, the coil is usually made to rotate within the field. As the coil rotates, it cuts through the flux lines, generating a voltage across the coil's terminals. When the face of the coil is parallel to the field, it cuts rapidly through the flux lines. But when the coil has turned 90 degrees and is perpendicular to the field lines, then the motion of the coil is tangential to the field and no voltage is produced. As the coil turns past this point, it cuts through the field in the opposite direction, generating a negative voltage. The end result of this chain of events is that the voltage produced by the generator varies as the cosine of the angle as shown below. This sinusoidal waveform is referred to as an alternating current or AC.

The equation for a waveform of this type is:

$$v(t) = A \cos(\omega t + \phi)$$ (1)

where $A$ is the amplitude, $\omega$ is the frequency, and $\phi$ is the phase . Since $v(t)$ is a time-varying voltage signal, $A$ has units of volts. The frequency has units of radians per second. Phase is measured in radians. We often measure frequency in a related unit of cycles per second. A cycle corresponds to $2 \pi$ radians.

The sinusoidal waveform in equation 1 is a periodic waveform. A signal $v$ is periodic if and only if there exists $T > 0$ such that $v(t)=v(t+T)$ for all $t$. To see if a sinusoidal waveform is periodic we therefore need to find $T$ such that

$$A \cos(\omega t + \phi) = A \cos(\omega (t+T) + \phi)$$ (2)

In particular, we know that the cosine function repeats every $2 \pi$ radians so we need to find $T$ such that

$$A \cos(\omega(t+T)+\phi) = A \cos(\omega t + 2 \pi + \phi)$$ (3)

Clearly this occurs if $\omega T = 2 \pi$ or rather

$$T = \frac{2 \pi}{\omega}$$ (4)

is the fundamental period of this sinusoidal function.

The size of a sine wave can be measured in a variety of ways. We may, for instance, use the waveform's amplitude ($A$) to specify the waveform's size. Another measure of "size" is the signal's root mean square or rms strength

$$\mbox{RMS} = \left[ \int_{0}^{\omega/2 \pi} \left( A \cos(\omega t + \phi) \right)^2 dt \right]^{1/2}$$ (5)

Since generators naturally produce sine waves, these waveforms play an important role in electrical engineering. It also turns out that sine waves also provide an efficient way of transporting electrical energy over a long distance. This is part of the reason why AC voltages are used in international power grids and, of course, this is why your wall socket provides a 120 volts (rms) AC voltage at 60 Hz.

In contrast to AC voltages, batteries provide a direct current or DC voltage. DC voltages are constant over time. In order to obtain DC voltages from an AC wall socket we're going to have to find some way of regulating the AC power source.