Calculus with MATLAB

Nancy K. Stanton

based on original versions © 2000-2005 by Paul Green and Jonathan Rosenberg, modified with permission

Contents

In this published M-file, we show how to represent functions of one varaible in MATLAB,then how to do symbolic computation, numerical computation and plotting with them.

Functions and Symbolic Differentiation

There are two distinct but related notions of function that are important in Calculus. One is a symbolic expression such as sin(x) or x^2. The other is a rule (algorithm) for producing a numerical output from a given numerical input or set of numerical inputs. This definition is more general; for example, it allows us to define a function f(x) to be x^2 if x is negative or 0, and sin(x) if x is positive. On the other hand, any symbolic expression implies a rule for evaluation. That is, if we know that f(x) = x^2, we know that f(4) = 4^2 = 16. In MATLAB, the fundamental difference between a function and a symbolic expression is that a function can be called with arguments and a symbolic expression cannot. However, a symbolic expression can be differentiated symbolically, while a function cannot. MATLAB functions can be created in three ways:

A typical way to define a symbolic expression is as follows:

syms x
f = x^2 - sin(x)

 
f =
 
x^2 - sin(x)
 

The next line shows we can differentiate f in the obvious way. MATLAB recognizes what the "variable" is. In the case of several symbolic variables, we can specify the one with respect to which we want to differentiate.

diff(f)

 
ans =
 
2*x - cos(x)
 

However, we cannot evaluate it, at least in the obvious way. If we type f(4)

we get an error message:

??? Error using ==> mupadmex Error in MuPAD command: Index exceeds matrix dimensions.

Error in ==> sym.sym>sym.subsref at 1366 B = mupadmex('mllib::subsref',A.s,inds{:});

We can evaluate f(4) by substituting 4 for x using the subs command:

subs(f,x,4)

ans =

   16.7568

We can also turn f into an inline function with the command:

fin=inline(char(f))

fin =

     Inline function:
     fin(x) = x^2 - sin(x)

What's going on here is that the inline command requires a string as an input, and char turns f from a symbolic expression to the string 'x^2-sin(x)'. (If we had simply typed fin=inline(f) we'd get an error message, since f is not a string.) The inline function fin now accepts an argument:

fin(4)

ans =

   16.7568

In MATLAB 7, the best way to make f into function is with the @ operator, creating an anonymous function. We can create such a function with

fanon = @(t) subs(f, x, t)
fanon(4)

fanon = 

    @(t)subs(f,x,t)


ans =

   16.7568

Similarly we can construct a function, either inline or anonymous, from the derivative of f:

fxin=inline(char(diff(f)))

fxin =

     Inline function:
     fxin(x) = 2*x - cos(x)

Here the matlab function char replaces its argument by the string that represents it, thereby making it available to functions such as inline that demand strings as input.

Alternatively, we can try:

fxanon = @(t) subs(diff(f), x, t)
fxanon(4)

fxanon = 

    @(t)subs(diff(f),x,t)


ans =

    8.6536

The other way to create a function that can be evaluated is to write a function M-file. This is the primary way to define a function in most applications of MATLAB, although we will not use it oftern. The M-file can be created with the MATLAB editor, and you can print out its contents with the type command.

type fun1

function y = fun1(x)
 y = x.^2 - sin(x)

fun1(4)

y =

   16.7568


ans =

   16.7568

Problem 1

Let g(x) = x(e^x - x - 1).

Graphics and Plotting

One of the things we might want to do with a function is plot its graph. MATLAB's most elementary plot operation is to plot a point with specified coordinates.

plot(4,4)

The output from this command is the faint blue dot in the center of the figure. The way MATLAB plots a curve is to plot a sequence of dots connected by line segments. The input for such a plot consists of two vectors (lists of numbers). The first argument is the vector of x-coordinates and the second is the vector of y-coordinates. MATLAB connects dots whose coordinates appear in consecutive positions in the input vectors. Let us plot the function we defined in the previous section. First we prepare a vector of x-coordinates

X1=-2:.5:2

X1 =

  Columns 1 through 8

   -2.0000   -1.5000   -1.0000   -0.5000         0    0.5000    1.0000    1.5000

  Column 9

    2.0000

X1 is now a vector of nine components, starting with -2 and proceeding by increments of .5 to 2. We must now prepare an input vector of y-coordinates by applying our function to the x-coordinates. Our function fin will accomplish this, provided that we "vectorize" it, i.e., we redefine it to be able to operate on vectors.

The matlab function vectorize replaces , ^, and / by ., .^, and ./ respectively. MATLAB works primarily with vectors and matrices, and its default interpretation of multiplication, division, and exponentiation is as matrix operations. The dot before the operation indicates that it is to be performed entry by entry, even on matrices, which must therefore be the same shape. There is no difference between the dotted and undotted operations for numbers. Vectorized expressions are not symbolic; they cannot usually be symbolically differentiated.

fin=inline(vectorize(f))
Y1=fin(X1)
plot(X1,Y1)

fin =

     Inline function:
     fin(x) = x.^2 - sin(x)


Y1 =

  Columns 1 through 8

    4.9093    3.2475    1.8415    0.7294         0   -0.2294    0.1585    1.2525

  Column 9

    3.0907

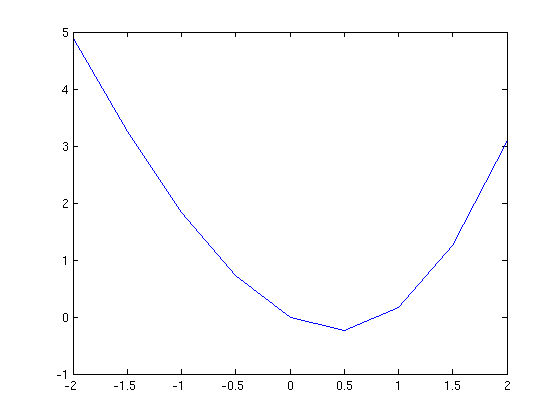
This plot is somewhat crude; we can see the corners. To remedy this we will decrease the step size. We will also insert semicolons after the definitions of X1 and Y1 to suppress the output.

X1=-2:.02:2;
Y1=fin(X1);
plot(X1,Y1)

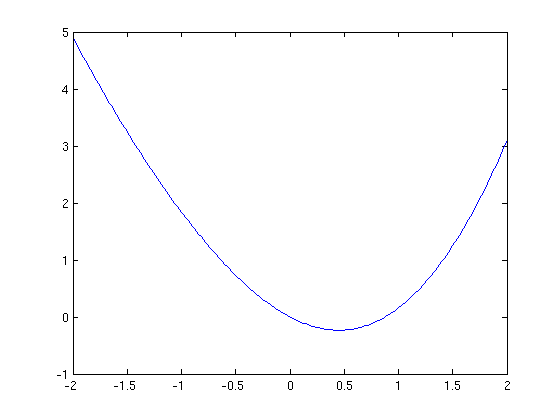
Actually, the plotting of a symbolic function of one variable can be can be accomplished much more easily with the command ezplot, as in Introduction to MATLAB. However, plot allows more direct control over the plotting process, and enables one to modify the color, appearance of the curves, etc. (Type doc plot for more on this.)

Problem 2

Let the function g be as in Problem 1.

Solving Equations

The plot of f indicates that there are two solutions to the equation f(x) = 0, one of which is clearly 0. We have both solve, a symbolic equation solver, and fzero, a numerical equations solver, at our disposal. Let us illustrate solve first, but with an easier example. Since we are looking for roots of g, so we will call the roots groots.

g = x^2 - 7*x + 2
groots = solve(g)

 
g =
 
x^2 - 7*x + 2
 
 
groots =
 
 7/2 - 41^(1/2)/2
 41^(1/2)/2 + 7/2
 

Here solve finds all the roots it can, and reports them as the components of a column vector. Ordnarily, solve will solve for x, if present, or for the variable alphabetically closest to x otherwise. In the next example, y specifies the variable to solve for. Notice also that the first argument to solve is a symbolic expression, which solve sets equal to 0.

syms y
solve(x^2+y^2-4, y)

 
ans =
 
  (2 - x)^(1/2)*(x + 2)^(1/2)
 -(2 - x)^(1/2)*(x + 2)^(1/2)
 

Unfortunately, solve will not work very well on our function f, and may even cause MATLAB to hang. Let us try fzero instead, which solves equations numerically, using something akin to Newton's method, starting at a given initial value of the variable. The command fzero will not accept f as an argument, but it will accept the construct @fun1 (the @ is a marker for a function name) or an anonymous function.

newfroot=fzero(char(f),.8)
newfroot=fzero(fin,.8)
newfroot=fzero(fanon,.8)

newfroot =

    0.8767


newfroot =

    0.8767


newfroot =

    0.8767

Sometime solve gives the answer in an unexpected form.

solve(2*sin(x)-x-1/2)

 
ans =
 
matrix([[0.55659293573136694255367405673316581]])
 

Here the answer is in the form of a matrix (so it has one column and 1 row) names ans. It's entry is ans(1).

Now you can check that you really have solved the equation:

subs(2*sin(x)-x-1/2,x,ans(1))

 
ans =
 
0.0
 

Problem 3

Let g be as in Problems 1 and 2.

Symbolic and Numerical Integration

We have not yet dealt with integration. MATLAB has a symbolic integrator, called int, that will easily integrate f.

intsf=int(f,0,2)

 
intsf =
 
cos(2) + 5/3
 

However, if we replace f by the function h, defined by

h=sqrt(x^2-sin(x^4))

 
h =
 
(x^2 - sin(x^4))^(1/2)
 

then int will be unable to evaluate the integral.

int(h,0,2)

Warning: Explicit integral could not be found.  
 
ans =
 
int((x^2 - sin(x^4))^(1/2), x = 0..2)
 

However, if we type double (standing for double-precision number) in front of the integral expression, MATLAB will return the result of a numerical integration.

double(int(h,0,2))

Warning: Explicit integral could not be found.  

ans =

    1.7196

We can check the plausibility of this answer by plotting h between 0 and 2 and estimating the area under the curve.

ezplot(h,[0,2])

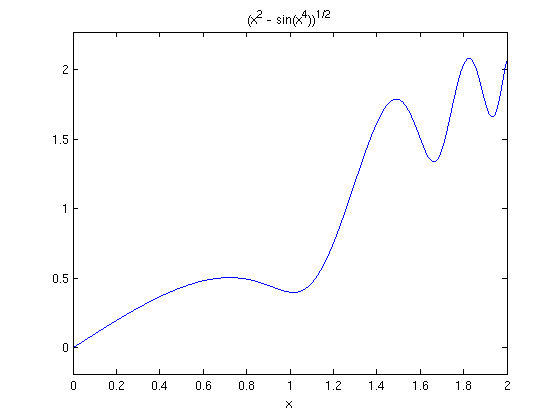
The numerical value returned by MATLAB is somewhat less than half the area of a square 2 units on a side. This appears to be consistent with our plot.

The numerical integration invoked by the combination of double and int is native, not to MATLAB, but to Mupad, from which MATLAB's symbolic routines are borrowed. MATLAB also has its own numerical integrator called quadl. (The name comes from quadrature, an old word for numerical integration, and the "l" has something to do with the algorithm used, though there's no need for us to discuss it here). The routines double(int(?)) and quadl(?) give slighly different answers, though usually they agree to several decimal places.

quadl(@(x) eval(vectorize(h)),0,2)

ans =

    1.7196

Problem 4

Let g be as in previous problems.

symbolically, using int, and numerically using quadl. Compare your answers.

both using int and double, and using quadl.

Additional Problems

1. Let f(x) = x^5 + 3x^4 - 3x + 7.

2. Find all real roots of the equation x = 4 sin(x). You will need to use fzero.

3. Evaluate each of the following integrals, using both int and quadl.

a)

b)

Published with MATLAB® 7.9