Section 6.2- The Runge-Kutta Method

In Problem Set C #16 I have asked you to implement the fourth order Runge-Kutta method in MATLAB, which I'll refer to as the Runge-Kutta method. Here I use my implementation, which I called rungekutta, to find a numerical solution of

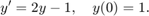
$y' = 2y -1, \quad y(0) = 1.$

rungekutta takes the same input as myeuler.

f = @(t,y) 2*y - 1;

First I use step size 0.1.

[t1,y1] = rungekutta(f, 0, 1, 0.4, 4); [t1 y1]

ans =

         0    1.0000
    0.1000    1.1107
    0.2000    1.2459
    0.3000    1.4111
    0.4000    1.6128

Next I use step size 0.05.

[t2,y2] = rungekutta(f, 0, 1, 0.4, 8); [t2 y2]

ans =

         0    1.0000
    0.0500    1.0526
    0.1000    1.1107
    0.1500    1.1749
    0.2000    1.2459
    0.2500    1.3244
    0.3000    1.4111
    0.3500    1.5069
    0.4000    1.6128

I will make a table of values at t = 0, 0.1,...,0.4. I will include the exact solution, which is

syms t
y = dsolve('Dy = 2*y - 1, y(0) = 1', 't')

 
y =
 
exp(2*t)/2 + 1/2

I will also include the approximate solution I had obtained with Euler's method using step size 0.025.

[ta,ya] = myeuler(f, 0, 1, 0.4, 16); ya

Here is the table. The first column is t, the second ya, the third y1, the fourth y2 and the last y.

T = [ ]
for k = 0:4
    digits(9)
    A = [vpa(t1(k+1)),vpa(ya(4*k+1)),vpa(y1(k+1)),vpa(y2(2*k+1)),...
        vpa(subs(y,'t',t1(k+1)))];
    T = [T;A];
end
[sym('t1'),sym('ya'),sym('y1'),sym('y2'),sym('y');T]

T =

     []

 
ans =
 
[  t1,         ya,         y1,         y2,          y]
[   0,        1.0,        1.0,        1.0,        1.0]
[ 0.1, 1.10775312,     1.1107, 1.11070129, 1.11070138]
[ 0.2, 1.23872772, 1.24590898, 1.24591212, 1.24591235]
[ 0.3, 1.39792816, 1.41105323, 1.41105898,  1.4110594]
[ 0.4, 1.59143729, 1.61276041, 1.61276978, 1.61277046]

Here is a table of the errors. The second column is the error with Euler's method, the third is the Runge-Kutta method with step size 0.1 and the fourth is the Runge-Kutta method with step size 0.05.

T = [ ]
for k = 0:4
    digits(9)
    A = [vpa(t1(k+1)),vpa(subs(y,'t',t1(k+1)))-vpa(ya(4*k+1)),...
        vpa(subs(y,'t',t1(k+1)))-vpa(y1(k+1)),...
        vpa(subs(y,'t',t1(k+1)))-vpa(y2(2*k+1))];
    T = [T;A];
end
[sym('t1'),sym('Ea'),sym('E1'),...
    sym('E2');T]

T =

     []

 
ans =
 
[  t1,            Ea,               E1,                 E2]
[   0,             0,                0,                  0]
[ 0.1, 0.00294825408, 0.00000137908008, 0.0000000936547379]
[ 0.2, 0.00718462693, 0.00000336882064,  0.000000228780293]
[ 0.3,  0.0131312372, 0.00000617202325,  0.000000419149289]
[ 0.4,  0.0213331701,   0.000010051357,  0.000000682600077]

I see that with step size 0.1 the Runge-Kutta method gives errors that are less than 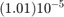$(1.01)10^{-5}$ . With step size 0.05 it gives errors that are less than 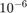$10^{-6}$ . With step size 0.025, Euler's method gives an error greater than 0.02 at t=0.4.