Section 6.4

Contents

Kinky graph produced by ode45

Sometimes a solver will use too large a step size and produce a kinky plot. This can happen, e.g., if there is a lot of oscillation in the solution.

Here I use ode45 with its default settings to solve 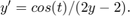$y'=cos(t)/(2y-2).$

f = @(t,y) cos(t)/(2*y-2);
[ta,ya]= ode45(f,[0 30],3);
plot(ta,ya,'k')

The kinkyness isn't coming from errors in the values computed; it's coming from not computing enough points. To get rid of the kinky appearance of the plot produced by ode45. I can use odeset to force ode45 to compute more points.

options = odeset('Refine',20);
[ta2,ya2]=ode45(f,[0 30],3,options);
plot(ta,ya,'k')
hold on
plot(ta2,ya2,'r')
hold off

Contrast the default behavior of ode45 with the behavior in dfield8.

A stiff equation

I look at the equation 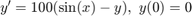$y'=100(\sin(x)-y),\ y(0)=0$. This is linear, so it's easy to solve exactly.

sol = dsolve('Dy=100*(sin(x)-y),y(0)=0','x');
pretty(sol)

exp(-100 x) 100   100 sqrt(10001) cos(x + atan(100))
--------------- - ----------------------------------
     10001                       10001

Notice that when 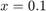$x=0.1$ the exponential term in this solution is less than 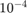$10^{-4}$ so the exponential term is already negligible by the time 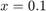$x=0.1$. However, as we see below, it still exerts a very strong influence on numerical solutions.

What happens when we use Runge-Kutta on $[0,3]$ to evaluate y(3)?

f = @(x,y) 100*(sin(x)-y)

f = 

    @(x,y)100*(sin(x)-y)

Here is the result using 100 steps, 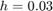$h=0.03$.

[t1,y1] = rungekutta(f,0,0,3,100);

y1(101)

ans =

   6.7289e+11

This is about 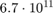$6.7 \cdot 10^{11}$ which doesn't pass the laugh test. The exact solution is the sum of three terms, the first two each with magnitude less than .01 and the last with magnitude less than 1.

Here is the result using 120 steps, 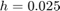$h=0.025$.

[t2,y2] = rungekutta(f,0,0,3,120);

vpa(y2(121),8)

 
ans =
 
0.15094317

Here is the result using 150 steps, 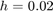$h=0.02$.

[t3,y3] = rungekutta(f,0,0,3,150);

vpa(y3(151),8)

 
ans =
 
0.15099613

Here is the result using 201 steps, 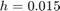$h=0.015$.

[t4,y4] = rungekutta(f,0,0,3,200);

vpa(y4(201),8)

 
ans =
 
0.15100303

Using 120, 150 and 200 give plausible answers which are not very far apart.

Here's what happens with ode45.

[t,ya] = ode45(f,[0 3],0);
vpa(ya(3),8)

 
ans =
 
0.00015956555

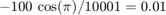This seems much too small. Since 3 is fairly close to $\pi$, I expect the answer to be much closer to $-100 \, \cos(\pi)/10001 = 0.01$.

A decimal approximation to the exact answer is

vpa(subs(sol,'x',3),8)

 
ans =
 
0.15100483


Published with MATLAB® R2015b