Differential Equations with MATLAB
Contents
Using MATLAB to give a numerical solution to an ODE
The ODE is
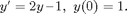
We use ode45 to obtain the numeric solution. We have to define a MATLAB function equal to the right side of the equation, which we can do with an anonymous function.
syms t
f = @(t,y) 2.*y -1
f =
@(t,y)2.*y-1
To solve and plot the approximate solution ya on the interval [0,1], we give the command
ode45(f, [0,1], 1)
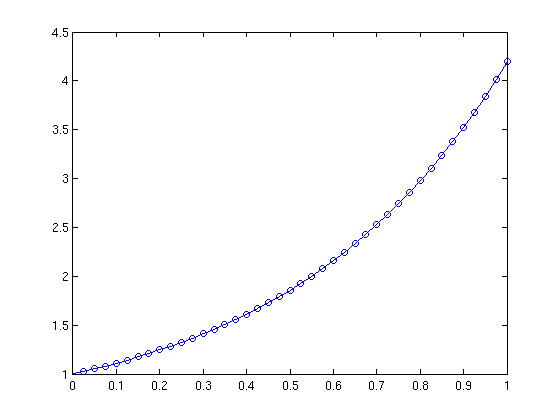
The second argument is the interval and the last one is the value of the solution at the left end of the interval.
This equation is linear, so it is easy to solve symbolically.
dsolve('Dy = 2*y-1, y(0)=1','t')
ans = exp(2*t)/2 + 1/2
We can make a table of values of the approximate and exact solutions. We don't want an enormous table, so we only calculate at t=0,0.1,0.2,...,1. The first column in the table is t, the second the value of the approximate solution, and the third the value of the exact solution.
[t,ya] = ode45(f,0:0.1:1,1);
y = 1./2+1./2.*exp(2.*t);
format long
[t,ya,y]
ans =
0 1.000000000000000 1.000000000000000
0.100000000000000 1.110701386666667 1.110701379080085
0.200000000000000 1.245912367353179 1.245912348820635
0.300000000000000 1.411059434148805 1.411059400195255
0.400000000000000 1.612770519540847 1.612770464246234
0.500000000000000 1.859140998650765 1.859140914229523
0.600000000000000 2.160058585103081 2.160058461368274
0.700000000000000 2.527600159740712 2.527599983422337
0.800000000000000 2.976516458318416 2.976516212197557
0.900000000000000 3.524824070395758 3.524823732206473
1.000000000000000 4.194528508426800 4.194528049465325
The approximate and exact solutions agree to 6 decimal places. This is a contrast with the result we had for the same equation when we used Euler's method.