Differential Equations with MATLAB Chapter 8

Using ode45 to find a vertical asymptote

Using ode45 to find a vertical asymptote

We look at the equation

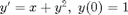
$y' = x + y^2,\ y(0)=1$

What happens when we look for an exact solution?

syms x
y = dsolve('Dy = x + y^2, y(0)=1', 'x'); pretty(y)

                  airyAi(-x, 1) #1
  airyBi(-x, 1) - ----------------
                         #2
  --------------------------------
                  airyAi(-x, 0) #1
  airyBi(-x, 0) - ----------------
                         #2
  
  where
  
                2/3      1/2           2
     #1 = 2 pi 3    - 3 3    gamma(2/3)
  
                1/6               2
     #2 = 2 pi 3    + 3 gamma(2/3)

The solution invoves two types of Airy functions. It isn't very easy to see what it means. What happens when we plot the numeric solution obtained using ode45?

f = @(x,y) x+y^2;
[t,ya] = ode45(f,[0,1],1);
plot(t,ya)

Warning: Failure at t=9.305611e-01.  Unable to meet integration tolerances without
reducing the step size below the smallest value allowed (1.776357e-15) at time t.

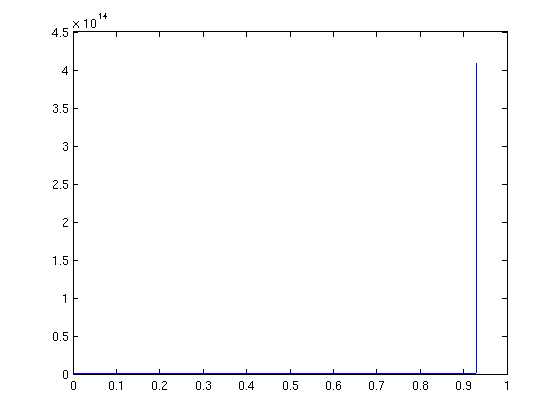
It has a vertical asymptote between 0.9 and 0.95. We'll plot it on some smaller intervals.

[t,ya] = ode45(f,[0,0.9],1);
plot(t,ya)

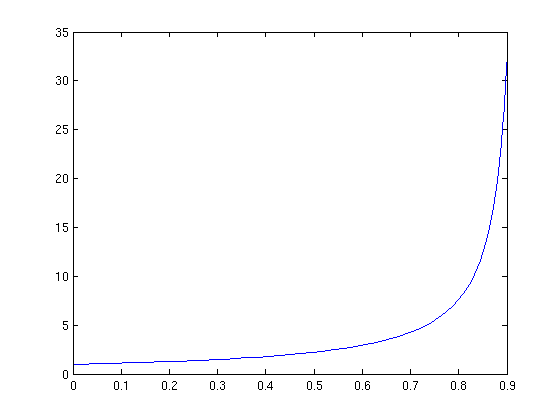
[t,ya] = ode45(f,[0,0.95],1);
plot(t,ya)

Warning: Failure at t=9.305618e-01.  Unable to meet integration tolerances without
reducing the step size below the smallest value allowed (1.776357e-15) at time t.

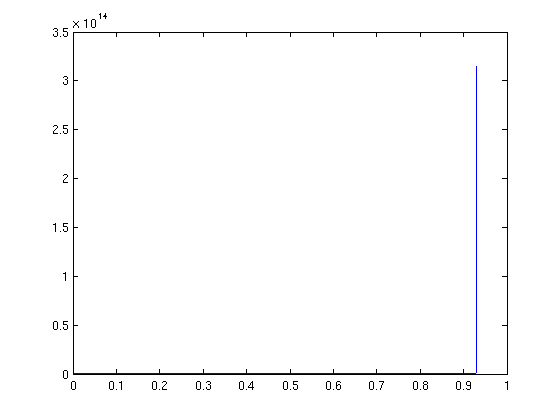
[t,ya] = ode45(f,[0,0.93],1);
plot(t,ya)

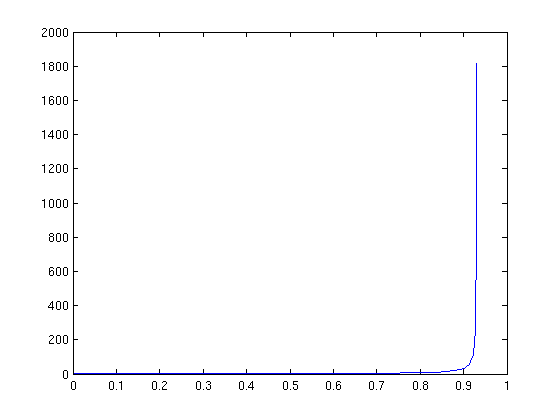
[t,ya] = ode45(f,[0,0.94],1);
plot(t,ya)

Warning: Failure at t=9.305485e-01.  Unable to meet integration tolerances without
reducing the step size below the smallest value allowed (1.776357e-15) at time t.

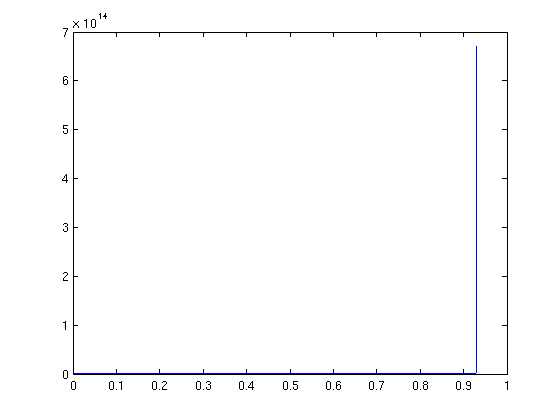
The asymptote is at about t=0.93. You can zoom in to get a better idea.

Differential Equations with MATLAB Chapter 8

Contents

Using ode45 to find a vertical asymptote