USING MATLAB TO SOLVE A HIGHER ORDER ODE
Here is an example of using MATLAB to solve an inhomogeneous higher order differential equation. The equation is:
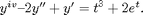
eqn = 'D4y - 2*D2y + Dy = t^3 +2*exp(t)'
eqn = D4y - 2*D2y + Dy = t^3 +2*exp(t)
The notation D4y means the 4th derivative of y, Dky means the kth derivative (where k is a positive integer).
I can solve this equation with the command dsolve. I'll call the solution sol. I'll supress printing it, because the answer will give too long a line, then use the command pretty to print it, which will make it fit reasonably.
sol = dsolve(eqn); pretty(sol)
4
2 3 t C9
C7 - 6 t + C10 exp(t) + 2 t exp(t) - 3 t - t - -- + C8 #1 + -- -
4 #2
/ / 1/2 1/2 1/2
| / t \ | 2 5 C7 54 5 t 87 5
| exp| - + #4 | | C7 - 24 t + 3 exp(t) - --------- + --------- + ------- +
\ \ 2 / \ 5 5 5
1/2 2 1/2 3 1/2 2 3 4 \ \
33 5 t 7 5 t #3 7 5 exp(t) 15 t 3 t t | |
---------- + --------- + -- - ------------- - ----- - ---- - -- - 39 | | / #2 -
10 10 10 5 2 2 4 / /
/ / t \ 1/2 1/2 1/2
| exp| - - #4 | #1 (120 t - 20 C7 + 4 5 C7 + 72 5 t + 96 5 +
\ \ 2 /
1/2 2 1/2 3 1/2 2 4 \
12 5 t + 8 5 t - #3 - 16 5 exp(t) + 60 t + 5 t + 240) | /
/
1/2
(20 (3 5 - 7)) - 6
where
/ / 1/2 \ \
| | 5 | |
#1 = exp| t | ---- - 1/2 | |
\ \ 2 / /
/ / 1/2 \ \
| | 5 | |
#2 = exp| t | ---- + 1/2 | |
\ \ 2 / /
1/2 4
#3 = 5 t
1/2
5 t
#4 = ------
2
In this case, the answer appears much too complicated. The next thing to try is simplify.
pretty(simplify(sol))
4
2 3 t
42 t - C7 - 6 exp(t) + C10 exp(t) + 2 t exp(t) + 12 t + 2 t + -- +
4
/ 1/2 \
| 5 t |
C8 exp| ------ |
\ 2 / C9
---------------- + ---------------------- + 72
/ t \ / 1/2 \
exp| - | / t \ | 5 t |
\ 2 / exp| - | exp| ------ |
\ 2 / \ 2 /
I can also try simple.
pretty(simple(sol))
/ 1/2 \
| t (5 - 1) | C9
42 t - C7 - 6 exp(t) + C10 exp(t) + C8 exp| ------------ | + ------------------- +
\ 2 / / 1/2 \
| t (5 + 1) |
exp| ------------ |
\ 2 /
4
2 3 t
2 t exp(t) + 12 t + 2 t + -- + 72
4
This has the terms in a different order from the previous answer but isn't simpler.
Notice that the equation is fourth order and the solution depends on 4 constants, C7, C8, C9 and C10.