SOLVING A HIGHER ORDER INITIAL VALUE PROBLEM

Here is an example of how you can use MATLAB to solve an initial value problem.

Section 4.2 #31

Find the solution of the inital value problem

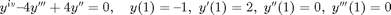
$y^{iv} \mbox{--} 4 y''' + 4 y'' = 0,\quad y(1)=\mbox{--}1,\ y'(1)=2,\ y''(1)=0,\ y'''(1)=0$

and plot its graph. How does the solution behave as t tends to infinity?

Here are the equation and initial conditions.

eqn = 'D4y - 4*D3y + 4*D2y = 0'
ic  = 'y(1) = -1, Dy(1)=2, D2y(1)=0, D3y(1)=0'

eqn =

D4y - 4*D3y + 4*D2y = 0


ic =

y(1) = -1, Dy(1)=2, D2y(1)=0, D3y(1)=0

I use dsolve to solve the problem. This time, I give it a second argument, the initial conditions. I also tell dsolve what the independent variable is. If the equation only involves one variable, this isn't essential. If the equation involves more than one and you want to think of the others as parameters, it is essential to tell MATLAB which is the independent variable.

sol = dsolve(eqn,ic,'t')

 
sol =
 
2*t - 3

I'll use ezplot to plot the solution. (Of course this one is easy to plot by hand.)

ezplot(sol)

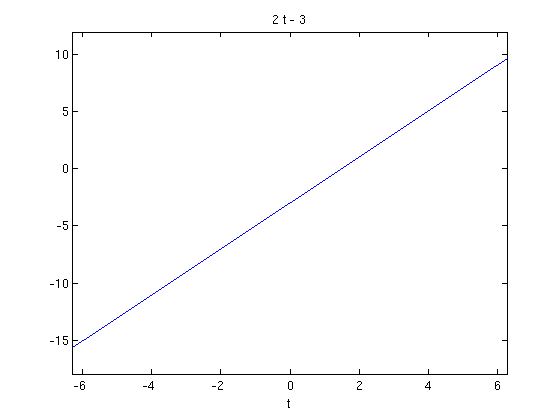
The solution tends to infinity as t tends to infinity - it grows linearly.