Section 10.6 Problem 9

The problem is to solve the heat equation in a 20 cm aluminum bar (so 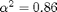$\alpha^2 = 0.86$ ), with initial value 25, u(0,t)=0, u(20,t)=60 for t>0.

The first step is to find a steady state solution v with v(0,t)=0, v(20,t)=60. The solution is v=3x. Write u = v+w, so w = u-v solves the heat equation with homogeneous boundary conditions and initial value 25 -3x. Let b(n) be the nth coefficient in the Fourier sine series of 25-3x.

syms x t n k
b = @(n) int(2*(25-3*x)*sin(n*pi*x/20),x,0,20)/20;

The temperature at time t is

u = @(x,t,n) 3*x + symsum(b(k)*exp(-0.86*k^2*pi^2*t/400)*sin(k*pi*x/20),k,1,n);

with $n = \infty$ .

I plot the initial value, the steady state solution, and the solution at two other times, using n=3.

X = 0:.04:20;
U = inline(vectorize(u(x,t,3)));
plot(X,3.*X,'r')
hold on
plot(X,U(5,X),'g')
plot(X,U(50,X),'k')
ezplot(25+0*x,[0,20])
hold off
legend1 = legend({'t=Steady state','t=5','t=50','Initial value'},'Position',[0.1625 0.6967 0.1957 0.1869]);
title('')

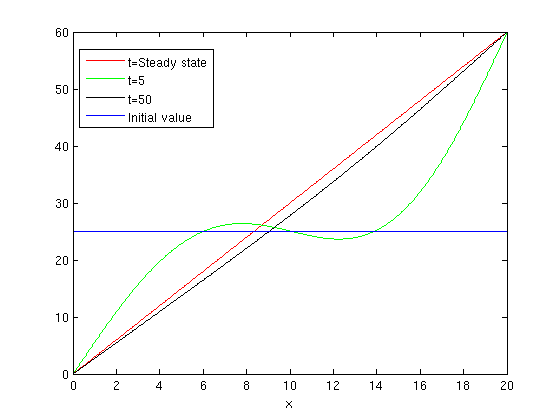
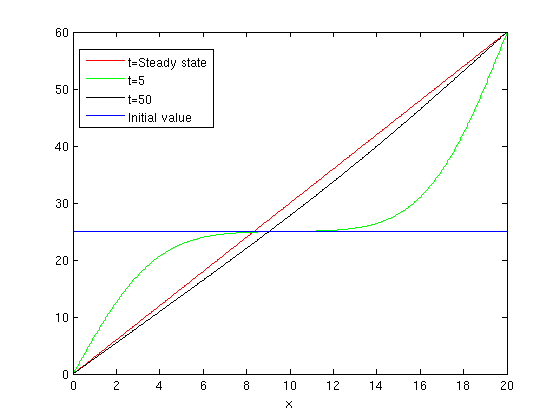
Now I see what happens if I take n=10.

U = inline(vectorize(u(x,t,10)));
plot(X,3.*X,'r')
hold on
plot(X,U(5,X),'g')
plot(X,U(50,X),'k')
ezplot(25+0*x,[0,20])
hold off
legend1 = legend({'t=Steady state','t=5','t=50','Initial value'},'Position',[0.1625 0.6967 0.1957 0.1869]);
title('')

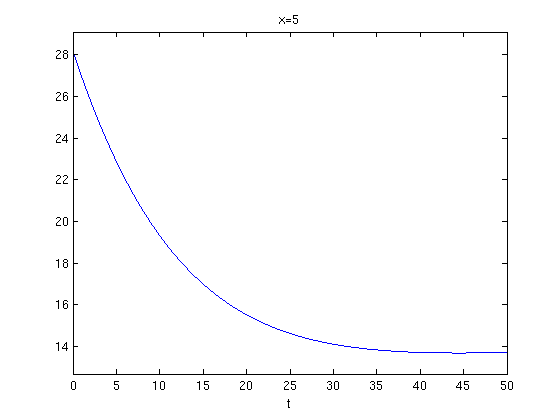
Next I plot u as a function of t for certain values of x.

ezplot(u(5,t,3),[0,50])
title('x=5')

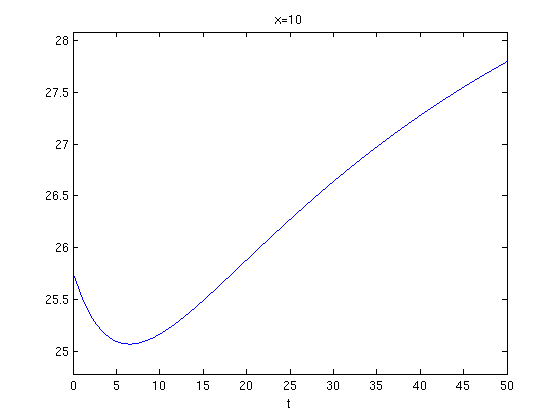
ezplot(u(10,t,3),[0,50])
title('x=10')

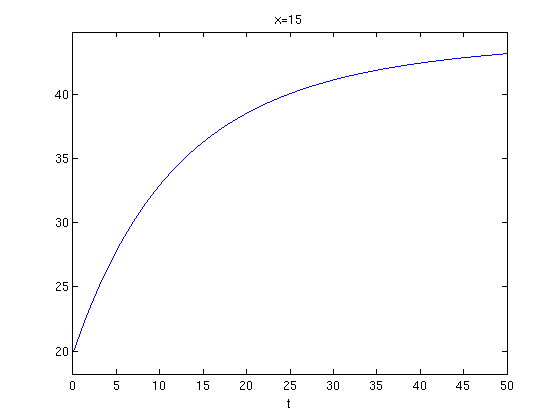
ezplot(u(15,t,3),[0,50])
title('x=15')

Next I find where the first term in the series is within 1% of the steady state temperature (which is 3*5=15) at x=5. The first term is u(5,t,1)

which is within f = 15 - u(5,t,1) of the steady state solution. So, I want to find when 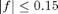$|f|\le 0.15$ .

f = 15 - u(5,t,1);
double(solve(f-0.15,t))

ans =

  160.3018