SECTION 4.3 - THE METHOD OF UNDETERMINED COEFFICIENTS
Contents
Here I solve the inhomogeneous fifth order ODE
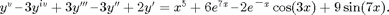
Solving by hand (letting MATLAB do each calculation)
First I have MATLAB carry out the same steps I would do if I were solving it by hand. Then I see what happens if I ask MATLAB to solve the original equation.
Here is a MATLAB function (defined by a function-M file) which will apply the left side of the equation to a function f.
type diffop
function [L] = diffop(f,x)
% DIFFOP applies the differential operator L which takes y to y^v - 3y^{iv} + 3y'''- 3y'' + 2y' to the
% function f(x). It requires two arguments, a function and an independent variable.
L = diff(f,x,5) - 3*diff(f,x,4) + 3*diff(f,x,3) - 3*diff(f,x,2) + 2*diff(f,x);
The first step is to solve the corresponding homogeneous equation, by plugging
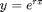
into the left side.
syms r x L = diffop(exp(r*x),x)
L = 2*r*exp(r*x) - 3*r^2*exp(r*x) + 3*r^3*exp(r*x) - 3*r^4*exp(r*x) + r^5*exp(r*x)
I divide the left side by exp(rx). I have to give the simplify command to get MATLAB to carry out the division.
charpoly = simplify(L/exp(r*x))
charpoly = r*(r^2 + 1)*(r - 1)*(r - 2)
Now I have to find the roots of the characteristic polynomial. solve assumes the right side of the equation is 0.
roots = solve(charpoly)
roots = 0 1 2 i -i
I know that 1, exp(x), exp(2x), cos(x) and sin(x) form a fundamental set of solutions of the homogeneous equation.
The right side of the equation has 4 terms, each of a different form, so I break the inhomogeneous problem into 4 problems. For the first, the right side is x^5. So, since 1 solves the homogeneous equation, I look for a solution of the form y_1 equal to x times a polynomial of degree 5. Here is a loop which builds it.
y_1 = 0; for k = 0:5 vars{k+1} = ['a' num2str(k)]; u = vars{k+1}* x^(6-k); y_1 = u + y_1; end y_1
y_1 = a0*x^6 + a1*x^5 + a2*x^4 + a3*x^3 + a4*x^2 + a5*x
I plug it into the left side and subtract x^5. The expression is very lengthy. It helps to use collect to collect all the terms involving the same power of x (and factor the power out of the terms) and to use pretty so it doesn't run off the screen.
Y = collect(diffop(y_1,x) - x^5,x); pretty(Y)
5 4 3
(12 a0 - 1) x + (10 a1 - 90 a0) x + (360 a0 - 60 a1 + 8 a2) x +
2
(180 a1 - 1080 a0 - 36 a2 + 6 a3) x + (720 a0 - 360 a1 + 72 a2 - 18 a3 + 4 a4) x +
120 a1 - 72 a2 + 18 a3 - 6 a4 + 2 a5
I want to solve the system of equations that I get from setting the coefficents equal to 0. I can either do this by copying and pasting the coefficients into the solve command or using a for loop to calculate the coefficients and set them equal to 0. Here I use a loop to do it. The value of the coefficient of x^j is the jth derivative of Y evaluated at 0. The corresponding equation is indexed by j+1.
for k = 1:6 eqn = subs(diff(Y,x,k-1),x,0); eqns{k} = [char(eqn) '=0']; end
Now I solve the resulting system.
range = 1:6;
sol = solve(eqns{range},vars{range});
for k = range
vals{k} = sol.(vars{k});
end
I substitute these into y_1.
Y_1 = subs(y_1,vars,vals)
Y_1 = x^6/12 + (3*x^5)/4 + (15*x^4)/8 + (15*x^3)/4 + (285*x^2)/8 + (765*x)/8
I verify that this is a solution. To get MATLAB to do the algebra after applying the left side to Y_1, I have to use simplify.
simplify(diffop(Y_1,x))
ans = x^5
The right side of the second equation is 6 exp(7x), which doesn't solve the homogeneous equation so I look for a solution of the form
syms a
y_2 = a*exp(7*x)
y_2 = a*exp(7*x)
I plug it into the left side of the equation and subtract 6 exp(7x). This time I want to collect the terms involving exp(7x).
Y = collect(diffop(y_2,x)-6*exp(7*x),exp(7*x))
Y = (10500*a - 6)*exp(7*x)
I need the coefficient of exp(7x).
C = coeffs(Y,exp(7*x))
C = 10500*a - 6
I solve this equation.
[a] = solve(C)
a = 1/1750
I evaluate y_2 using this.
Y_2 = eval(y_2)
Y_2 = exp(7*x)/1750
I verify that this is a solution.
diffop(Y_2,x)
ans = 6*exp(7*x)
The third term on the right is - 2exp(-x)cos(3x) which doesn't solve the homoegeneous equation, so I look for a solution of the form
clear a syms a b y_3 = a*exp(-x)*cos(3*x)+b*exp(-x)*sin(3*x)
y_3 = (a*cos(3*x))/exp(x) + (b*sin(3*x))/exp(x)
I plug this into the left side of the equation and subtract - 2exp(-x)cos(3x) When I do this, every term will contain a factor of exp(-x), so I divide the result by that.
Y = simplify((diffop(y_3,x) + 2*exp(-x)*cos(3*x))/exp(-x))
Y = 2*cos(3*x) + 330*a*sin(3*x) - 300*b*sin(3*x) - 300*a*cos(3*x) - 330*b*cos(3*x)
I could get the equations by evaluating Y and its derivative at 0. Instead I will use coeffs command. I notice that Y is a linear "polynomial" in cos(3x) and sin(3x), so I want the coefficients of cos(3x) and of sin(3x).
E1 = coeffs(Y,cos(3*x))
E1 = [ 330*a*sin(3*x) - 300*b*sin(3*x), 2 - 330*b - 300*a]
The coefficient of cos(3x) is the second term in E1
eq1 = E1(2)
eq1 = 2 - 330*b - 300*a
Now I find the coefficient of sin(3x).
E2 = coeffs(Y,sin(3*x)); eq2 = E2(2)
eq2 = 330*a - 300*b
I solve the resulting equations using solve. The solve command assumes that the right side of each equation is 0.
[a,b] = solve(eq1,eq2); [a,b]
ans = [ 2/663, 11/3315]
I evaluate y_3 using this.
Y_3 = eval(y_3)
Y_3 = (2*cos(3*x))/(663*exp(x)) + (11*sin(3*x))/(3315*exp(x))
I verify that this solves the equation.
diffop(Y_3,x)
ans = -(2*cos(3*x))/exp(x)
The last term on the right is 9 sin(7x). This doesn't solve the homogeneous equation so I look for a solution of the form
clear a b syms a b y_4 = a*cos(7*x) + b*sin(7*x)
y_4 = b*sin(7*x) + a*cos(7*x)
I plug this into the left side of the equation and subtract 9 sin(7x).
Y = diffop(y_4,x) - 9*sin(7*x)
Y = 15792*b*cos(7*x) - 15792*a*sin(7*x) - 7056*b*sin(7*x) - 7056*a*cos(7*x) - 9*sin(7*x)
Again I use coeffs to get the equations.
E1 = coeffs(Y,cos(7*x)); eq1 = E1(2)
eq1 = 15792*b - 7056*a
E2 = coeffs(Y,sin(7*x)); eq2 = E2(2)
eq2 = - 15792*a - 7056*b - 9
I solve the equations.
[a,b] = solve(eq1,eq2)
a = -141/296800 b = -9/42400
The resulting solution of the equation is
Y_4 = eval(y_4)
Y_4 = - (141*cos(7*x))/296800 - (9*sin(7*x))/42400
I verify that it solves the equation.
diffop(Y_4,x)
ans = 9*sin(7*x)
The resulting particular solution of the original equation is obtained by adding these 4 solutions.
y_p = Y_1 + Y_2 + Y_3 + Y_4; pretty(y_p)
2 3 4
765 x 141 cos(7 x) exp(7 x) 9 sin(7 x) 2 cos(3 x) 285 x 15 x 15 x
----- - ------------ + -------- - ---------- + ---------- + ------ + ----- + ----- +
8 296800 1750 42400 663 exp(x) 8 4 8
5 6
3 x x 11 sin(3 x)
---- + -- + -----------
4 12 3315 exp(x)
Solving with Matlab
What happens if you let MATLAB solve the equation?
eqn = 'D5y - 3*D4y + 3*D3y - 3*D2y + 2*Dy= x^5 + 6*exp(7*x) - 2*exp(-x)*cos(3*x) + 9*sin(7*x)'; Y = dsolve(eqn, 'x'); pretty(simple(Y))
765 x C18 141 cos(7 x) exp(7 x) 9 sin(7 x)
----- - --- - ------------ + -------- - ---------- + C19 cos(x) + C22 exp(x) +
8 2 296800 1750 42400
2 3 4 5 6
2 cos(3 x) 285 x 15 x 15 x 3 x x
C20 sin(x) + ---------- + ------ + ----- + ----- + ---- + -- + C21 exp(2 x) +
663 exp(x) 8 4 8 4 12
11 sin(3 x)
----------- + 765/16
3315 exp(x)
This is a general solution of the equation. I compare it with our particular solution.
simplify(Y - y_p)
ans = C19*cos(x) - C18/2 + C22*exp(x) + C20*sin(x) + C21*exp(2*x) + 765/16
I get a solution of the homogeneous equation, which is what I should get.