CREATING A MOVIE OF CONVERGENCE OF A FOURIER SERIES

Contents

Creating a movie

The command fourier_movie will create an animation or movie of the first n partial sums of the Fourier series of the expression f on the interval [a,b]. You will want to download fourier_movie.m to use it. Here is the code for the command.

type fourier_movie

function fsm = fourier_movie(f,x,a,b,n)

% This animates the first n partial sums of the Fourier series of the 
% symbolic expression f(x) on the interval [a,b].  The function is assumed 
% to be periodic with period L = b-a.
L = (b-a);
X = a:0.001:b;
g = inline(vectorize(f));

partsum = 1/L * double(int(f,x,a,b));
for k =1:n 
    partsum = partsum ...
        + 2/L*double(int(f*sin(2*k*pi*x/L),x,a,b))*sin(2*k*pi*x/L) ... 
        + 2/L*double(int(f*cos(2*k*pi*x/L),x,a,b))*cos(2*k*pi*x/L);
    ps2 = inline(vectorize(partsum));
    plot(X,g(X),'r'); hold on
    plot(X,ps2(X)); hold off
    fsm(k) = getframe;
end

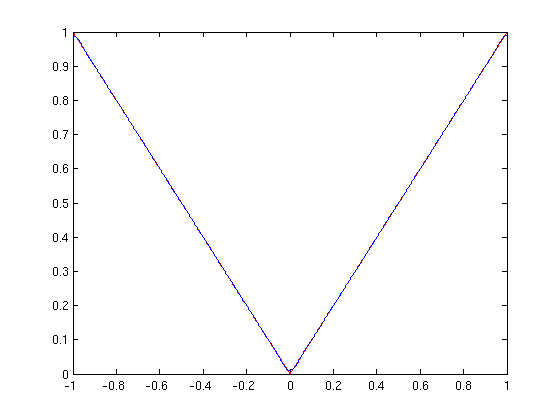
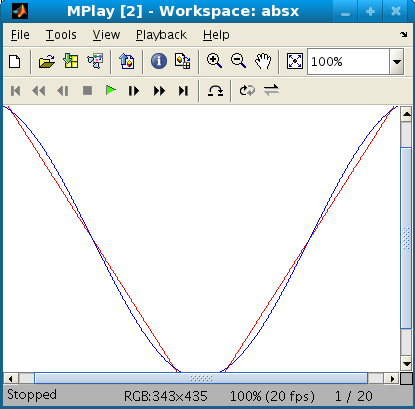
Example 1: |x|

syms x
f = abs(x); a= -1; b=1; n=20;

This command creates the movie.

absx = fourier_movie(f,x,-1,1,20);

Viewing the movie

You can view it with mplay.

mplay(absx)

Saving the example

You can save it as name.mat (replace "name" by the name you want) with the command save('name','mymovie') where mymovie is the name you gave the output of your fourier_movie command. Then you can load it during another MATLAB session with the command load('name'). The movie will then be named 'mymovie'. This command saves the example as absx.mat.

save('absx','absx')

You can use different names for the two arguments in the save command, but when you load name.mat with the command load('name'), the movie will be named mymovie.

You can close mplay windows with the command

close all hidden

Example 2: x

Since the convergence of the series is slower for this function, we take the first 50 partial sums.

f = x
xmovie = fourier_movie(f,x,-1,1,50);

 
f =
 
x
 

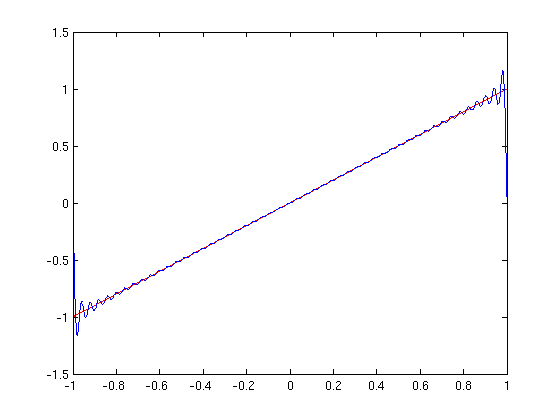
mplay(xmovie)

close all hidden

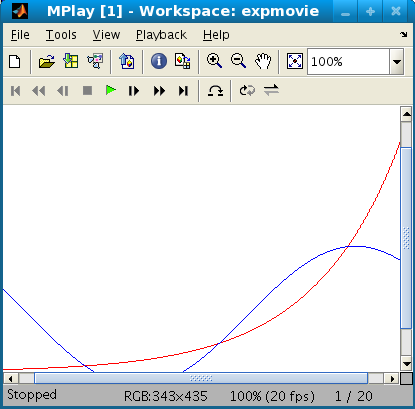
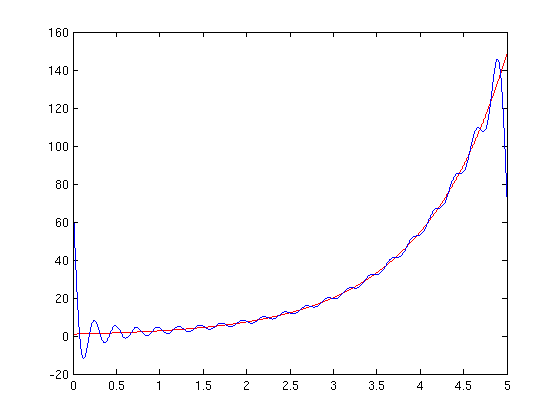
Example 3: exp(x)

I'll take 20 partial sums on [0,5].

f = exp(x)
expmovie = fourier_movie(f,x,0,5,20);

 
f =
 
exp(x)
 

mplay(expmovie)

Published with MATLAB® 7.10