Mensural notation     Around the year 1260, the music theorist Franco of Cologne wrote a treatise called the Ars cantus mensurabilis (“The Art of Measured Song”), explaining the principles of the new art of measured music that had been evolving in the previous decades. In it he set forth a system of notation that would remain the basic practice for writing music other than chant until the seventeenth century. It is a system similar to modern notation in many respects, but with several significant differences.    Franco’s primary goal was to remove as much as possible the ambiguities inherent in the previous system of writing measured music, the so-called “modal” notatation, which indicated by the arrangement of binary and ternary ligatures—and sometimes ligatures of more than three notes—each of six possible rhythmic modes. In modal notation, a ligature could be broken by a change of syllable or by a repeated pitch, rendering what would otherwise have been ligated difficult or impossible to determine. A single isolated note produced by the breaking of a ligature could then assume up to four different durational interpretations, depending on what other notes and ligatures surrounded it. A further problem: The built-in ambiguities of the system made reading it a slow and uncertain process. Note Taruskin’s point that the collections of clausulae we have in the great Notre Dame polyphonic anthologies were musical models for early motets, where the ligatures had not yet been broken up by the addition of words. Reading these early motets thus necessiated having them notated in two different forms, one with the words, one without. Hence the motivation to devise a system where a single note shape would have a single meaning, whether texted or not.    Franco’s note shapes are the ancestors of those in use today. Although they were square and diamond-shaped rather than round, they functioned in many ways just as modern note shapes do. One great difference, however, is that for Franco notes could only be triply divided. Duple division of notes, the ubiquitous practice of modern notation, did not become a recognized part of mensural practice until the fourteenth century with Philippe de Vitry’s treatise, the Ars nova (ca. 1320). Secondly, for Franco the only note values that received official recognition were the long, the short, and the semi-short (longa, brevis, semibrevis). Even the semibreve received little attention, the focus falling almost entirely on longs and shorts.    There are two main branches of Franconian teaching, one having to do with the rules of perfection/imperfection and alteration, the other treating the construction and interpretation of ligatures. Perfection was the quality a note possessed when it was complete, i.e., composed of three of the next smaller note. Thus, a perfect long consisted of three breves (and, by implication, a perfect breve consisted of three semibreves). A perfect note could be imperfected by a smaller note under certain conditions, in which case the note that had been imperfected would equal only two-thirds of its value before imperfection. A long imperfected by a following (or preceding) breve would thus be equal to two breves, with the breve that had imperfected it making up for the value lost. An imperfected long and a following (or preceding) breve would then together have the value of a perfect long. 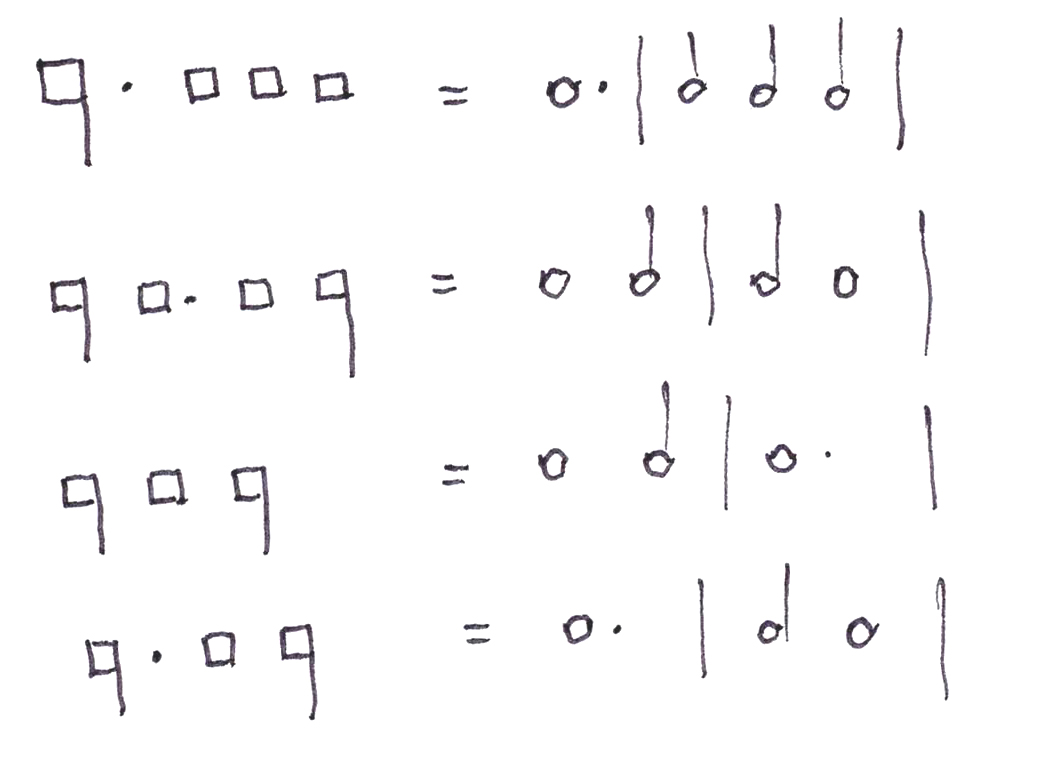   An obligatory rule of imperfection was like the forced jump in checkers: if a smaller note could imperfect a larger note it was required to do so. There were three situations, however, in which a smaller note was prevented from imperfecting a larger one. 1) when a dot of separation prevented a breve following a long from imperfecting the long. 2) When three breves occurred between two longs, the three breves were to be considered an integral unit equal to a perfect long. In this situation, none of the breves could imperfect either the long they followed or the long they preceded. 3) When two breves occurred between two longs, they too were to be considered an integral unit. (See more on this in the discussion of Similis ante similem below.)    A second obligatory rule stated that Similis ante similem perfecta est. This rule required a note prior to another note of the same size (referring primarily, in Franco’s system, to perfect longs) to be perfect. Thus, a long occurring before another long had to be perfect—no exceptions. Since this made the rhythm perfect long, breve, imperfect long, long impossible to notate, Franco’s system allowed for that rhythm to be notated as perfect long, breve, [altered] breve, long, with the altered breve lasting twice the value of a normal breve (i.e., the same value as an imperfect long), even though its shape was the same shape as that of a normal breve. Similis ante similem and alteration are two sides of the same coin. Alteration was used only to get around what would otherwise be the impossibility of writing the value of an imperfect long before another long.    Mensural notation used dots of division to separate one perfect note (or its equivalent in smaller notes) from another when there would otherwise be ambiguity. The following examples show a dot of division and two situations where a dot was not necessary: 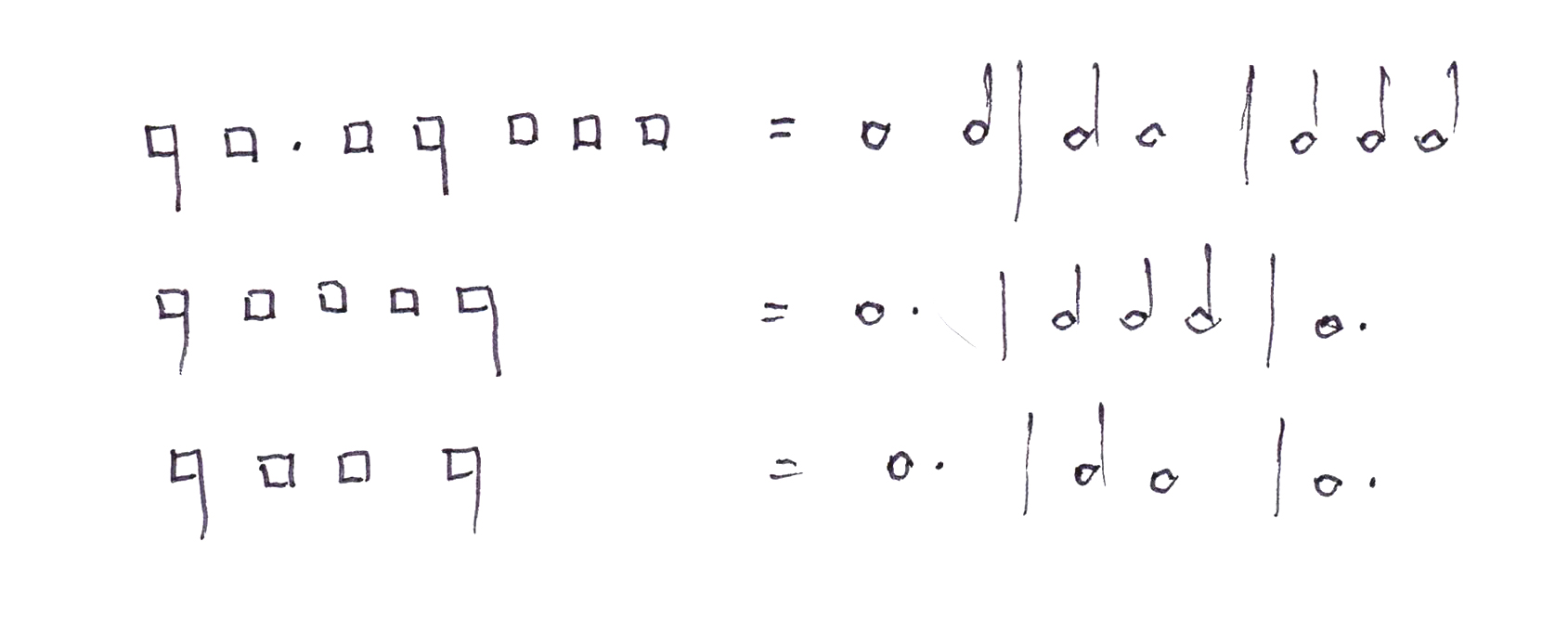   In the 1310s, a new note value was added to the system—the minim. Perfection was now possible at the level of the long, the breve, or the semibreve, with a perfect (or “major”) semibreve equaling three minims. Even shorter notes soon came into the system as well, e.g., the semiminim, the fusa, the dragma, and others, but perfection was generally reserved for longs, breves, and semibreves.     A great change brought to the system by the Ars nova was duple division of notes. A wholly duple division, where all notes were to be divided duply, functioned just as modern notation does, for the modern system is premised throughout on the duple division of notes, triple division being indicated by dots of addition. In duple mensurations, notes could not be imperfected, because they were imperfect to begin with. Nor was there any occasion for the use of alteration, since the Similis ante similem had no role in duple mensurations.     Dots had two functions: they could be dots of addition (also called dots of augmentation), which functioned as dots do in modern notation, where they increase the value of a note by half again its undotted value. Or they could be dots of division. Only context could distinguish a dot of division from a dot of addition.    The second great branch of Franco’s teaching had to do with the construction and interpretation of ligatures. A first principle was that the prime forms of two-note ligatures—two notes ascending or two notes descending—always had the value of breve, long. The prime two-note ligatures took their shape directly from quadratic chant notation, with the prime ascending two-note ligature looking like the podatus (or pes) of chant notation, in other words, of two notes, one on top of the other, joined by a stem on the right, and the prime descending two-note ligature looking like the flex (or clivis) of chant notation, in other words, of two notes, one to the right and lower than the other, joined by a stem extending from the right side of the first note to the left side of the second note. (If two descending notes were very close in pitch, no stem was necessary, because the two notes actually touched right side of upper note to left side of lower note.) The prime form of the descending two-note ligature also had a stem descending from the left side of the first note. 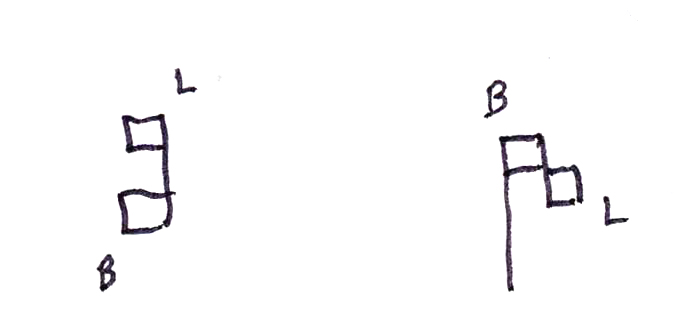   Franco referred to the prime forms as possessing propriety and perfection (not the same sort of perfection as was spoken of above). Thus a prime-form ligature was said to be cum propietate et cum perfectione, whereas a ligature that lacked these qualities was said to be sine proprietate et sine perfectione. It is not necessary to use Franco’s teminology here, which only causes confusion because of the two meanings of the term perfection. It is sufficient to point out that changing an essential feature of either note in a two-note ligature caused the note so changed to become the opposite of what it had been (the only possibilities for such notes being either short or long). Thus, if a descending stem were to be added to the right of the first note of a two-note ascending ligature, that first note would change to a long, and the resulting two-note ligature would be read as long, long. If the first note of this ligature were to be left in its prime form, but the second note were to be flipped around so that it faced away from the first note (instead of being situated directly over it), then the second note would have its value changed from long to breve, and the resulting ligature would be read as short, short. 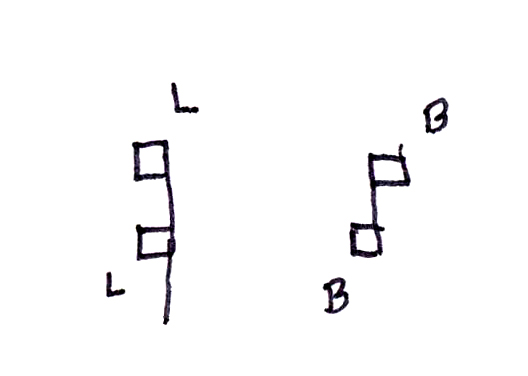    With descending two-note ligatures, the way to change the first note was to remove the descending stem to its left. A two-note descending ligature with everything the same as the prime form except for the removal of the initial descending stem would thus have the value of long, long. If the two square notes were to be replaced by a descending parallelogram, this change was considered to apply only to the second note. Thus, a descending parallelogram with a descending stem to its left would be read as short, short. Removing the descending stem to the left would cause such a parallelogram to be read as long, short. 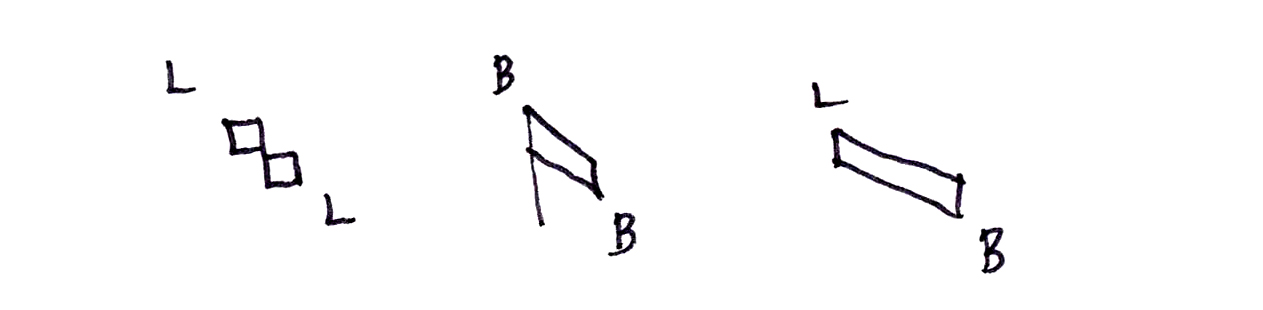    Should a middle note be inserted between the two notes of either of the prime forms, the middle note would be read as a breve. Indeed, if many such notes were to be inserted between the first and last note of a prime form, all such middle notes would be read as breves. In multi-note ligatures of this sort, the first note could be changed and/or the last note could be changed, but the middle note(s) would always be read as breves. Only if a descending stem were to be added to the right of a middle note would it change to a long. Thus, only the shape of the first and last note of a multi-note ligature had significance, all middle notes being read as breves, regardless of shape (e.g., whether square or part of a parallelogram), the only exception being the one just noted, where a descending stem might be added to the right of a middle note to change it from a breve to a long. 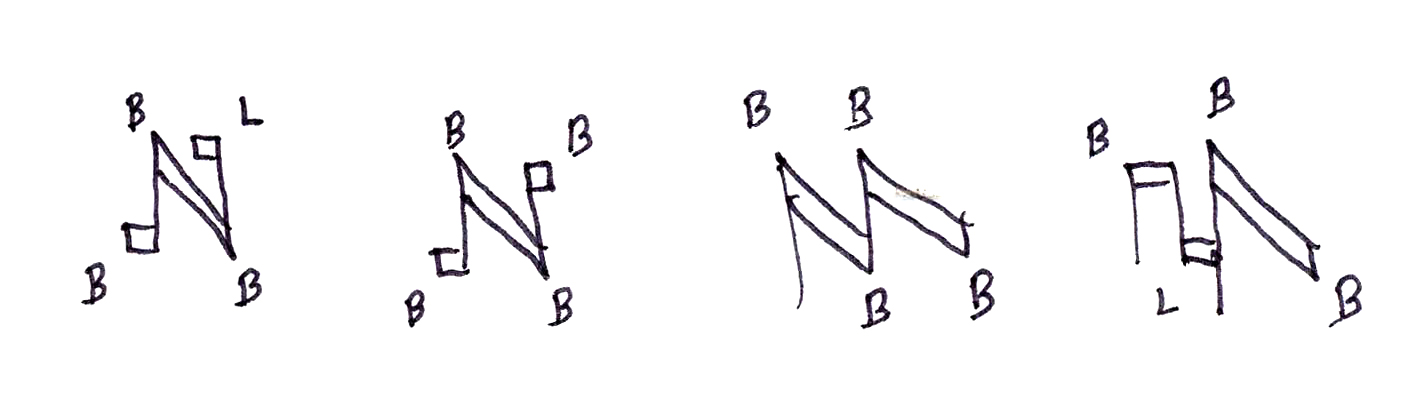    If one knows the prime form of the two-note ascending ligature and the prime form of the two-note descending ligature, all values in ligatures of whatever length or complexity can easily be determined using the rules above plus one other: if the stem to the left of a ligature ascends rather than descends, the ligature is said to be “cum opposita proprietate,” that is, to have a stem of propriety extending in the opposite direction of the prime form. A c.o.p. ligature, as it is called today, had its first two notes equal semibreves, regardless of their shape: 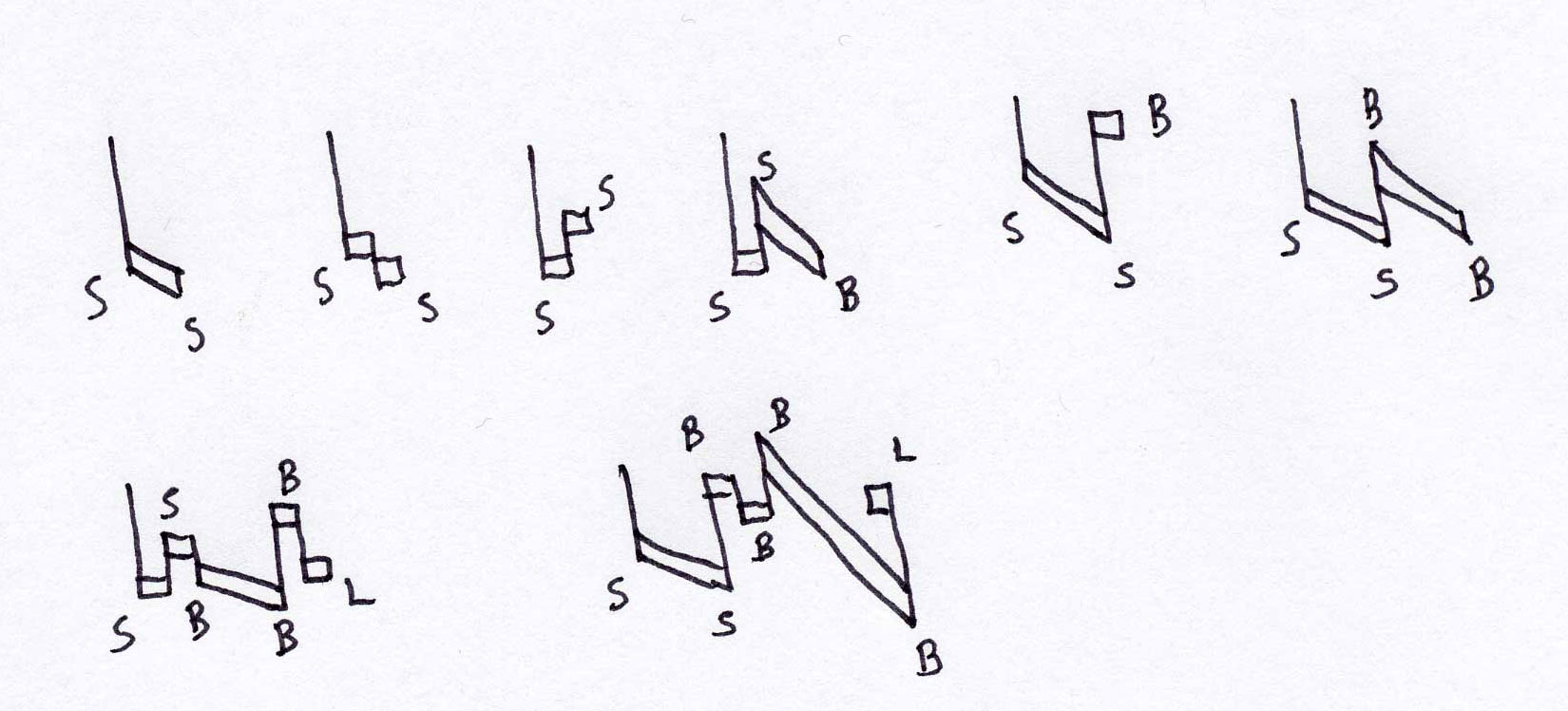    There were no mensuration signs in pure Franconian notation, because there was only one mensuration. Nor were signs used initially in Ars nova notation, which required the mensuration in use to be determined from the context of characteristic sequences of notes and rests. It is only at the beginning of the fifteenth century that we first see signs of mensuration beginning to appear in the sources of notated music. After a brief period of experimentation, the signs became stablilized with the following meanings:     [dotted circle]     A circle with a dot inside: the circle indicated that the breve (known as the tempus) was perfect, with the dot inside indicating that the semibreve was also perfect.     O     A circle without a dot inside: the circle indicated that the tempus was perfect, with the absence of the dot inside indicating that the semibreve was imperfect.     [dotted C]     An incomplete circle with a dot inside: the incomplete circle (usually referred to today as C) indicated that the tempus was imperfect, with the dot inside indicating that the semibreve was perfect.     C     An incomplete circle without a dot inside: the C indicated that the tempus was imperfect, with the absence of the dot inside indicating that the semibreve was also imperfect. Imperfection (duple division) of all values, as here, meant that the notes could almost be read as in modern notation.     As early as the second decade of the fourteenth century, we see a further notational device appear: the use of notes written in red ink to indicate a difference in value from notes written in black ink. After a brief period of experimentation, during which such pieces came equipped with rubrics to explain whether it was the black notes that were perfect and the red notes imperfect (or vice versa),1 the stabilized meaning came to be the former: black notes were to be read as perfect (or, in duple mensurations, as normal value); red notes were to be read as the removal of value from black notes (i.e., either as imperfected notes that had been perfect or, in duple mensurations, as triplets). When the mensuration in question had at least one value that was perfect, coloration, as the use of red ink was called, came to mean removal of a third of the value from perfect notes to create hemiolas. In a duple mensuration like C, coloration meant the removal of a third of the value of all notes to create triplets. 1 As in Philippe de Vitry’s motet Tuba sacre fidei/In arboris/Virgo sum, where the Tenor bears the Gregorian chant words Virgo sum, followed by the rubric Tenor. Nigre notule sunt imperfecte et rube sunt perfecte (“Tenor. The black notes are imperfect and the red ones perfect”). The interpretation of red notes in this work did not last. The dominant view came to be that red notes were imperfect, black notes perfect. RESTS The rests in mensural notation are the ancestors of today’s rests: A line that goes through an entire space represents a breve rest. A line that hangs from a line but does not go through an entire space is a semibreve rest. A line that sits on a line but does not go through an entire space is a minim rest. A line that sits on a line, does not go through an entire space, and has a flag at the top pointing to the left is a semiminim rest. A line that goes through two spaces represents a rest the value of two breves, or, to put it more correctly, the value of an imperfect long. A line that goes through three spaces represents a rest the value of three breves (= perfect long), as in the excerpt from the Old Hall Manuscript below.    Let us now look at the tenor of an Old Hall motet to see how Franconian rules, plus some innovations of the Ars nova, allow the rather complicated notation to be interpreted. The motet in question is Biteryng’s En Katerine solennia. The Tenor, notated once, is to be sung three times—with its notes in each statement accelerating in speed. The upper voices change mensuration twice as well, but they operate independently of the Tenor and to some extent independently of each other. While the upper voices each show mensuration signs—O for the first section of the voice that sings the “Virginalis concio” text, C for the voice that sings the “En Katerine” text—no such signs are provided for the Tenor, which must determine its relationship to the upper voices on the basis of context. The only notational devices in the Tenor beyond the shapes of notes and rests, the clef, and the signature of one flat, are the line through the whole staff to indicate the end of the statement, and, following that, a triple-repeat mark, :|||: , from which we learn that the Tenor is to be sung three times.    As we examine the makeup of the Tenor voice, we see that it begins with three breve rests stacked on top of one another, showing that the long is perfect. With the two upper voices sounding O against C simultaneously, a first guess as to the implied mensuration of the Tenor might be [dotted circle], but this proves to be incorrect, for the opening Tenor note F will then enter after its initial rests in the middle of a “measure” (if one can speak of measures in music notated without them); as the piece progresses, it becomes increasingly clear, because of the resulting dissonance, that [dotted circle] is not the right choice. The correct implied mensuration turns out to be [O]. Since the implied sign of [O] denotes a perfect breve worth 3 semibreves, this will require each perfect long worth 3 breves to have a total value of 9 semibreves.    In order to make sense of the Tenor’s sequence of note shapes, we need to look at the notation globally, and not simply proceed note by note. What we see is: perfect long rest, perfect long, breve, breve rest, perfect long, perfect long rest, a ligature consisting of breve, altered breve, perfect long, and then a single breve. At this point a passage in coloration is introduced, suggesting that we have reached the end of a perfection. The sequence of black notes and rests thus contains six perfect longs, plus a seventh when the two isolated breves are “completed” by the last uncolored note—the “missing” breve. The notation shows great sophistication and economy. The first two isolated breves have no dot of division between them. Had there been such a dot, the first breve would have imperfected the long it follows, and our first thought might be that the second breve (a rest) would imperfect the long that follows it. Yet this rest cannot imperfect that long, for the long is followed by a perfect long rest. Similis ante similem requires the long before another long to be perfect. We can approach the problem from another angle: lacking a dot of division, two breves between two perfect longs would normally be considered an indivisible unit, with the second breve altered. This, however, is prevented by the writing of the second breve as a rest. Since rests cannot be altered, we are forced to displace all perfect longs following the breve rest until the final note in the sequence-the single breve that is written just before the red notes—can “complete” the two isolated breves four perfect longs earlier.    The next five notes are written in red ink, indicating that they lose a certain amount of value. Since the black notes in the Tenor are pefect only at the level of the long, coloration (red ink) suggests several possibilities, e.g., imperfection would initially suggest imperfection the long. The dot of division, however, dividing the first two red notes from the three following, indicates that longs are still perfect; this suggests that the coloration removes value from the breves (and, as a result, the longs also). If a third of the value of the breves is removed, each red breve will be worth two semibreves, the imperfect red long will be worth four semibreves, and the perfect red long will be worth six semibreves. The values in coloration are long, breve, [dot of division], ligature consisting of breve, altered breve, long. Note that the implied semibreves in both black and red notation remain equal to one another (“implied semibreves,” because the Tenor has no notes smaller than a breve).     The Tenor now repeats all the values of notes and rests thus far, first with black notes, then with red ones, thereby establishing “isorhythm” in one complete statement, that is, with the entire rhythmic pattern exactly duplicated. Each half of this complete statement, containing 7 black notes and 5 red ones, constitutes what in the fourteenth century was called a talea, a complete rhythmic pattern. Therefore, each whole statement of the “Sponsus amat sponsam” Tenor contains two taleae. The Gregorian chant melody serving as the source of the Tenor’s pitches2 does not divide into halves, but rather extends, as a single 24-note melody with no internal repetitions of pitch groups, over the entire length of the Tenor statement. Such a complete melodic unit was known as a color. En Katerine’s Tenor voice is thus comprised of one color and two taleae. 2 The fragment is the beginning of a responsory for Matins on the Feast of St. Catherine of Alexandria, Virgin Martyr (November 25). The complete responsory can be found in __________________.     Looking, finally, at how Ars nova notation differed from Franco’s, the first point to be observed is that even before we consider the consequences of the appearance of minims into the system, we may note that breves could now behave as longs had previously. Thus, in O , the breve is perfect and can be imperfected by a semibreve. The placement of two semibreves between two perfect breves requires alteration of the second semibreve, etc. Everything works the same as in Franconian notation, but now down a level. In fact, everything works the same also down two levels, for semibreves as well as breves can function like Franco’s perfect longs. In a mensuration with perfect semibreves, such as [dotted circle] and [dotted C], it is the semibreves that are capable of being imperfected by minims. The placement of two minims between two perfect semibreves requires the second minim to be altered, etc. Theoretically, there are three levels where perfection can occur. Most pieces limit themselves to perfection at only one level, but occasionally we find a piece where both the breve and the semibreve are perfect at the same time. This can sometimes require alteration at two levels in close proximity. We also find coloration to produce hemiola being used to imperfect longs, breves, or semibreves, depending on the mensuration. With these minor modifications—and none at all to the rules for ligatures, which underwent virtually no change for over three centuries—Franco’s basic rules remained intact up to the seventeenth century; they simply had a wider application than Franco first afforded them at their unveiling ca. 1260.