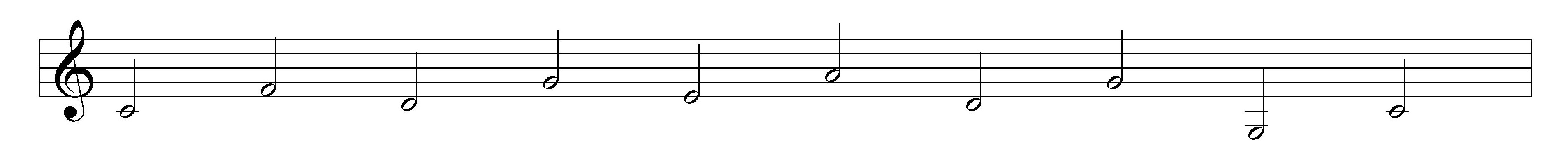Observations on Performance
by medieval and Renaissance Writers
|
From the De institutione musica (ca. 510 A.D.) of Boethius:
It can be easily proved that the power of numbers is prior to that of music.
Performers are mere slaves. A musician is he who commands a knowledge of the mathematical basis of the art.
Cited in Calvin M. Bower, Boethius' "The Principles of Music": an Introduction, Translation, and Commentary (Ph.D. dissertation, George Peabody College. 1966), p. 29
|
From the Musica disciplina (ninth century) of Aurelian of Réomé:
A mere singer seems to stand before a true musician as a prisoner before a judge.
Cited in Irving Godt, “New Voices and Old Theory,” Journal of Musicology 3: 312-19.
|
From the Prologus antiphonarii sui (early eleventh century) of Guido of Arezzo:
In our times, of all men, singers are the most foolish.
Cited in Irving Godt, “New Voices and Old Theory,” Journal of Musicology 3: 312-19.
|
From the De musica (ca. 1100) of Johannes (of Afflighem?):
The mere singer goes like a drunken man who does indeed get home but does not in the least know by what path he returns.
Cited in Irving Godt, “New Voices and Old Theory,” Journal of Musicology 3: 312-19.
|
From Irving Godt’s “New Voices and Old Theory” Journal of Musicology 3 (1984), 312-19:
Most of the scholars admitted to the pursuit of the Seven Liberal Arts in a Medieval university were, or expected to become clerics who would spend their lives in the church, and music was once an enormous part of the church’s business. A little simple arithmetic makes that truism especially impressive. If we multiply the number of musical items in the Mass (say, eleven) by the number of days in the year (ignoring duplications) we get a figure of 4,015 items. Taking the number of musical items sung each day in the Offices as 41 (again ignoring duplications), we get a total of 14,965. This massive total of 19,980 musical ’events’ per year does not include the 12,775 (or more) items sung to Psalm Tones, Lesson Tones, Gospel Tones, Canticle Tones, etc.; nor does it take account of special occasions such as baptisms, marriages, funerals, ordinations, etc. Even a non-musical cleric seeking preferment in the bureaucracy of the Medieval church might have had to supervise the organization, staffing, financing, or discipline of the vast and almost ceaseless musical activity of the churches within his administration. A theologian might have been inclined to grant more importance to the symbolic and speculative side of music, but he too might have had some responsibility for the day-to-day conduct of worship (which was mostly sung). It is difficult to imagine anything other than a fundamentally practical attitude toward music among churchmen—even among those scholar-clerics who wrote the most speculative treatises.
From Odo of Cluny (tenth century) down to John Dowland’s 1609 translation of Ornithoparcus, we encounter precise mechanical instructions for the calibration of a monochord so that it would sound true musical intervals. We may profitably digress here to remind ourselves that precise measurement is not a completely modern accomplishment. Galileo, for example, was able to make his observations of the acceleration of falling bodies without the benefit of modern chronometry thanks to the musical training he received from his father. If Ancient and Medieval musicians could not count vibration frequencies, their monochord allowed them to measure and to reproduce intervals as small as a syntonic comma, or about 1/9 of an equal tempered whole tone ( = 21.5 cents; a very sensitive ear can detect a difference as fine as 6 cents, less than a third of a comma).
We may feel some reluctance to recognize the monochord as a kind of “concerting” instrument, but the comment of Odo leaves no doubt that, as far as he was concerned, the monochord measured not only abstract theoretical intervals, but their performance by singers. It is needless to review here all the theorists who prescribe it, but Odo does not stand alone. More than half a millenium after him, writers continued to advocate it as a practical tool for teaching, not musical thinkers, but singers. Conrad von Zabern (fl. 1426-1474) appealed for a revival of the use of the monochord in the teaching of plainchant. Gafurius (1496) recommends that “it is exceedingly worthwhile for the human voice to imitate the harmonious strings that are sounded by the action of the lyre, cithara, or monochord.” For Ornithoparcus (1517) and for Dowland, his translator almost a century after him, the monochord still served as a basic teaching tool:
OF THE PROFIT OF THE MONOCHORD
The monochord was chiefly invented for this purpose,
to be the judge of Musical voices and intervals
as also to try whether the song be true or false;
furthermore, to show haire-braind Musitians their errors,
and the way of attaining the truth. Lastly that
children which desire to learn Musicke, may have
an easie meanes to it, that it may intice beginners,
direct those that be forward, and so make
of vnlearned learned.
Gafurius (and Dowland/Ornithoparcus) seem to imply by their choice that keyboard instruments (and the lute), because they usually required some kind of tempered tuning, could not satisfactorily answer their didactic purposes. All of the writers mentioned seem to have believed that the monochord alone produced those true sounds against which they expected singers to measure themselves.
Oliver Strunk, Source Readings in Music History (New York: W. W. Norton & Co., 1950), 106 n.: “A monochord made according to Odo’s directions will give the so-called Pythagorean intonation, the semitone (256/243) being obtained by subtracting the sum of two whole tones (9/8 plus 9/8 equals 81/64) from the fourth (4/3). Somewhat differently worded, Odo’s directions are given also by Guido in the Micrologus (GS, II, 4-5) and in the Epistola de ignoto cantu (GS II, 46).”
|
From the Practica musicae (1496) of Franchino Gaffurio:
Book 3, Chapter Three. The Eight Mandates or Rules of Counterpoint.
Nevertheless, this fifth, as organists maintain, permits the diminution of a small, concealed, and somewhat vague quantity which these organists call temperament.
Book 3, Chapter Fifteen. How a Singer Ought to Behave When He Performs.
Finally we are led to propose to young singers for the purpose of instruction and admonition that in performing they should not project their voices with an unusual and unsightly opening of their mouths, or with an absurd loud bellowing when they strive after melodies, especially in the divine mysteries. They should also spurn excessive vibrato and voices which are too loud, for they are not compatible with other voices similarly pitched. In short, because of their own continual instability they cannot maintain harmonious proportions with the other voices.
—Translated by Irwin Young, The Practica musicae of Franchinus Gafurius, Translated and edited with musical transcriptions (Madison, Milwaukee, and London: The University of Wisconsin Press, 1969), 133, 160.
Original Latin:
De Octo mandatis sive regulis Contrapuncti. Caput tertium.
Tamen quinta ipsa (quod organistae asserunt) minimae ac latentis incertaeque quodammodo quantitatis diminutionem patienter sustinet quae quidem ab ipsis participata vocatur.
Quomodo se regere debet cantor dum cantat. Caput quintumdecimum et ultimum.
Postremo novis cantoribus institutionis admonitionisque causa duximus proponendum: ne insolito et inhonesto oris hiatu aut ridiculo forte cachino voces proferant modulando: quum potissime in divinis misterijs modulos assequuntur: reiciant insuper et voces tremebundas atque perstrepentes: sunt enim sibi ipsis eadem extensione dissimiles: qua re caeteris vocibus proportionabiliter propter continuam ipsarum instabilitatem concordes esse non possunt.
— http://www.chmtl.indiana.edu/tml/15th/GAFPM3_TEXT.html
|
From Section II of the Musica theorica (1529) of Lodovico Fogliano:
Chapter 1. How Any Consonance May Be Matched to Its Proportion.
The ancients, and especially the Pythagoreans, matched only two genera of proportions to consonances: namely, the multiplex and the superparticular. From the multiplex they applied duple to the octave, triple to the octave and fifth, and quadruple to the double octave. In addition, they matched sesquialtera to the fifth and sesquitertia to the fourth. No other [intervals] than these did they consider to be consonances, as appears from their beliefs as we know them. But this position, notwithstanding that it arose from the greatest authority, nevertheless strikes me as false, for it contradicts the senses.
Who, unless he is deficient in the sense of hearing, can fail to find more consonances than the five just named? For within the octave are not beyond those [five] found the semiditone, the ditone, the minor
hexachord and the major hexachord; and outside the octave [beyond those five] found the octave plus semiditone and the octave plus ditone and the octave plus fourth, just as Ptolemy proposed? And also the octave plus hexachord and the octave plus major hexachord: these, which I am adding, are also consonances, and are called by those who practice music
the minor third, the major third, the minor sixth, the major sixth, the minor tenth, the major tenth, the eleventh, the minor
thirteenth, and the major thirteenth. For it cannot be denied that all these intervals are true and very agreeable consonances except by a denial of the senses, which is incongruous.
Moreover, all composers of polyphony in their compositions, and all organists, and all string players, and all singers without other skills, make use of consonances of this kind, as anyone who knows anything at all about this art realizes. I say, therefore, that many more consonances are found than the ancients posited, and that more than two genera of proportions can be matched to musical consonances.
On the contrary, all genera of proportions are found to be valid in producing them [consonances]. Indeed, it is necessary for the minor
hexachord and the major hexachord to be made from the superpartient genus; and for the octave plus ditone, the octave plus minor hexachord, the octave plus semiditone, and the octave plus fourth to be made from the multiplex superpartient genus; while the octave plus ditone, the
octave plus minor hexachord, and the octave plus major hexachord to derive their origin from the multiplex superparticular genus. Thus, it is definitely not the case that only two species of the superparticular genus may be matched to consonances. For beyond these are two others of this same species of genus, namely, sesquiquarta [5:4] and sesquiquinta [6:5], which generate the ditone and semiditone, as will be seen below. How any given consonance may be matched to its proportion is now to be
described. First we will speak concerning those derived from the multiplex, then those from the superparticular genus, and thus successively, observing the order of the genera.
Original Latin:
Sectio secunda. Quomodo unaquaeque consonantia suae aptetur proportioni. Caput Primum.
Duo tantum genera proportionum veteres et praesertim Pythagorici: ad musicas consonantias aptaverunt: videlicet. Multiplex: et superparticulare: ex multiplici quidem duplam ad Diapason: Triplam ad Diapasondiapente: et quadrumplam ad Bisdiapason applicantes: ex superparticulari vero: sesquialteram ad diapenten: et sesquitertiam ad Diatessaron fore aptas putavere: Nec plures his posuerunt consonantias: ut apparet ex suis quae ad nos pervenerunt opinionibus: Sed haec positio licet maxima innitatur auctoritate nihilominus mihi videtur falsa: quum sensui contradicat:
quis enim nisi sensu aurium diminutus neget plures alias a praedictis quinque: inveniri consonantias? Infra enim diapason nonne praeter istas invenitur: Semidytonus: Dytonus: Hexachordum minus: et Hexachordum maius: similiter supra Diapason: nonne invenitur Diapason cum semidytono: et Diapason cum dytono: et diapasondiatessaron: Quam posuit Ptholomaeus? Nec non diapason cum minori hexachordo: et diapson cum maiori hexachordo: hae autem quas addimus: sunt consonantiae: quae a practicis appellantur: Tertia minor: Tertia maior: Sexta minor: Sexta maior: Decima minor: Decima maior: Undecima: Tertiadecima minor: Tertiadecima maior: quae omnia intervalla esse veras et valde delectabiles consonantias non potest negari: nisi negato sensu: quod est inconveniens:
omnes enim concentuum auctores in suis compositionibus: similiter: Omnes organistae: Omnes cytharoedi: Et omnes naturaliter sine aliqua arte canentes huiusmodi utuntur consonantiis: ut scit quilibet in hac facultate mediocriter eruditus: Dicamus igitur quod multo plures: quam antiqui posuerint: inveniuntur consonantiae: et quod plura quam duo genera ad musicas consonantias aptari possunt:
immo omnia proportionum genera ad illas producendas valere comperiuntur: quippe hexachordum minus et hexachordum maius ex genere superpartienti fieri necesse est: diapason autem cum dytono: et diapason cum hexachordo minori: et diapason cum semidytono: et diapasondiatessaron ex multiplici superpartienti fieri necesse est: diapason autem cum dytono: et diapason cum hexachordo minori: et diapason cum hexachordo maiori ex multiplici superparticulari originem trahunt. Nec verum est etiam quod duae tantum generis superparticularis species sint ad consonantias aptae: sed praeter has sunt duae aliae eiusdem generis species scilicet sesquiquarta et sesquiquinta: quae dytonum generant et semidytonum:
ut infra patebit: Quomodo autem unaquaeque consonantia suae aptetur proportioni: nunc dicendum est: et primo de his quae ex multiplici: deinde: quae ex superparticulari oriuntur genere dicemus: et sic deinceps ordinem generum ad praesens observando: .
— http://www.chmtl.indiana.edu/tml/16th/FOLMUS2_TEXT.html
|
From Book 3 of the Le Istitutioni harmoniche (1558) of Gioseffo Zarlino,
titled The Art of Counterpoint:
Chapter 6. The Division of the Consonances into Perfect and Imperfect.
...The perfect are the unison, fourth, fifth, and octave, with their compounds.... The imperfect are the third, sixth, and their compounds.... Perhaps the perfect are so called because their intervals are determined by ratios contained in the number 4, and these proportions belong to the multiplex and superparticular classes. The number 4 (as I have said elsewhere) was held to be perfect by the Pythagoreans, because from its aliquot and nonaliquot parts, 4, 3, 2, 1, there resulted another number, which they called perfect: the number 10. Actually they called these perfect because, alone or accompanied by other consonances, they have the quality of satisfying the ear instantly and fully when it is affected by them. Whether placed high or low, provided it is in its true ratio, the perfect consonance so fortifies and pleases the ear that the sense desires nothing further to improve its sweet, welcome perfection....
The other consonances they called imperfect, for their ratios are those found in numbers beyond 4, namely 6, 5, 4. Thus the ditone springs from the proportion sesquiquarta [5:4] and the semiditone from the sesquiquinta [6:5], both in the superparticular class. These two intervals added to the diatessaron generate the sixths; that is, one forms the major and the other the minor sixth.
Chapter 10. The Property or Nature of the Imperfect Consonances.
The property or nature of the imperfect consonances is such that some of them are lively and cheerful, accompanied by great sonority; and others, although sweet and smooth, tend to be sad and languid. The former are the major third and sixth, with their compounds; the latter are the minor forms. All these have the capacity to alter every composition and to make it sad or cheerful, according to their respective natures. This may be seen from the fact that certain compositions are lively and full of cheer, whereas others on the contrary are somewhat sad and languid. In the first named the major imperfect consonances are often heard on finals or medians of certain modes or tones, namely the fifth, sixth, seventh, eighth, eleventh, and twelfth, as we shall see. These modes are very gay and lively, because in them the consonances are frequently arranged according to the nature of the sonorous number, that is, the fifth is harmonically divided into a major and minor third, which is very pleasing to the ear. [Note: The consonances are arranged according to the sonorous number when they occur in the order in which they are produced by the successive divisions of a string into 2, 3, 4, 5, and 6 parts. The fourth, fifth, and sixth divisions produce a series of notes in which a major third stands below a minor third. For example, if the string lengths that produce the three notes C, E, G are 30, 24, and 20, and the fifth is divided harmonically, the middle term is known as a harmonic mean. The three terms in a harmonic proportion are such that the proportion of the extremes is equal to the proportion of the differences. For example, in the series, 30, 24, 20, the differences 6 and 4 are in the same proportion as the extremes 30 and 20, namely 3:2.]
I say that the consonances are arranged according to the nature of the sonorous number because they are placed in their natural positions. Then the mode is gayer and greatly pleases the sense, which greatly appreciates and enjoys proportionate things, and despises and abhors the disproportionate. In the other modes, then, which are the first, second, third, fourth, ninth, and tenth, the fifth is divided otherwise. It is arithmetically divided by a middle note, in such a way that often one hears the consonances arranged contrary to the nature of the sonorous number. [Note: In an arithmetic series the difference between successive terms are equal. So the notes A, C, E, in the proportions 6:5:4, form an arithmetic series, and the fifth is divided by an arithmetic mean.]
Chapter 61. Common Rules.
...and [the third] must be major if the harmony is to be happier and fuller. Should it be minor, as it so often is, the harmony will be sadder.
—Translated by Guy A. Marco and Claude V. Palisca, Gioseffo Zarlino. The Art of Counterpoint. Part Three of Le Istitutioni harmoniche, 1588 (New York: Da Capo Press, 1983), 15-16, 21-22, 196.
Original Italian:
La Terza Parte Delle Istitutioni harmoniche di M. Gioseffo Zarlino da Chioggia, nella quale si ragiona della seconda parte della Musica chiamata prattica, cioe del l’Arte del Contrapunto.
Divisione delle consonanze nelle Perfette, & nelle Imperfette. Cap. 6.
...Le perfette sono l’Unisono, la Quarta, la Quinta, la Ottava, & le replicate.... Le Imperfette sono la Terza, la Sesta & quelle che nascono da queste aggiunte alla Ottava.... Et dicono le prime esser perfette, forse per che hanno la lor forma dalle proportioni contenute tra il numero Quaternario, nel genere Moltiplice, & nel Superparticolare, tra 4. 3. 2. 1. il qual numero (come altrove hò detto) appresso i Pithagorici era tenuto Perfetto: percioche dalle sue parti aliquote, & non aliquote, che sono i quattro mostrati numeri, risultava un’altro numero, il quale medesimamente chiamavano Perfetto, che è il Denario. Ma in vero le nominarono Perfette: conciosia che poste da per sè, overamente accompagnate ad altre consonanze, hanno posanza al primo apprenderle, che fà il sentimento, di acchetarlo, & satisfarli a pieno, quando da lor è mutato: Imperoche mentre se ne ode alcuna posta nel grave, over nello acuto, contenuta nella sua vera forma; fortifica l’Udito, & fà che niente desidera più oltra, che faccia alla sua perfettione, & la faccia più soave, & più grata.
Della propietà, o natura delle consonanze Imperfette. Cap. 10.
Il propio, o Natura delle Consonanze imperfette è, che alcune di loro sono vive & allegre, accompagnate da molta sonorità; & alcune, quantunque siano dolci, & soavi, declinano alquanto al mesto, overo languido. Le prime sono le Terze, & le Seste maggiori, & le replicate; & le altre sono le minori. Tutte queste hanno forza di mutare ogni cantilena, & de farle meste, overo allegre secondo la lor natura. Il che potemo vedere da questo; che sono alcune cantilene, le quali sono vive, & piene de allegrezza; & alcune altre per il contrario, sono alquanto meste, over languide. La cagion è, che nelle prime, spesso si odeno le maggiori consonarnze imperfette, sopra le chorde estreme finali, o mezane de i Modi, o Tuoni; che sono il Quinto, il Sesto, il Settimo, l’Ottavo, l’Undecimo, & il Duodecimo; come vederemo al suo luogo; i quali Modi sono molto allegri, & vivi; Conciosia che in essi si odono spesse fiate le consonanze collocate secondo la natura del numero sonoro, cioè la Quinta tramezata, o divisa harmonicamente in una Terza maggiore, & in una minore; il che molto diletta all’udito.
Dico le Consonanze esser poste in essi secondo la natura del numero sonoro: percioche allora le consonanze sono poste ne i loro luoghi naturali; onde il Modo è più allegro, & porge molto piacere al sentimento, che molto gode, & si diletta delli soggetti proportionati; & per il contrario, hà in odio, & aborisce li [di]sproportionati. Ne gli altri Modi poi, che sono il Primo, il Secondo, il Terzo, il Quarto, il Nono, & il Decimo, la Quinta si pone al contrario, cioè mediata arithmeticamente da una chorda mezana; di modo che molte volte si odeno le consonanze, poste contra lea natura del Num ero sonoro. Per il che, si come ne I primi, la Terza maggiore si spottopone spesse volte all minore; cosi ne I secondi si ode spesse fiate il contrarioi, & si ode un non so che di mesto, l languido, che rende tutta la cantilena molle; il che tanto più spesso si ode, quanto più spesso in esse sono poste a tal modo; per sequir la natura, & la propietà del Modo, nel quale è composta la cantilena.
Regole in commune. Cap. 61.
...& debbe esser a maggiore; accio che’l concento sia più allegro, & più pieno: ma se’l si abbatterà, che ella sia la minore; come infinite volte suole accascare, allora il concento sarà più mesto.
http://www.digital.library.unt.edu/ark:/67531/metadc25955/m1/169/sizes/xl/
Commentary on Zarlino by Albert Seay, reviewing the translation above:
Zarlino does not throw away the past completely. He accepts the importance of proportion as a coordinating element in the universe, tying together the heavenly spheres, the four elements, the seasons, as well as the parts of the body and the soul. But he does not accept the supremacy of four as the limiting number, preferring instead six or the senario, from which he derives his set of consonances. To most older theorists, the basic ratios were those laid down by Boethius, 1:1 (unison), 2:1 (octave), 3:2 (fifth) and 4:3 (fourth); to these was added that of the tone, 9:8, and from them all other intervals were derived by addition or subtraction. For Zarlino, the ratios for the first four intervals remained the same, but he added 5:4 (major third) and 6:5 (minor third). This was not new, for Bartolomeo Ramos had already suggested this kind of tuning in his Musica Practica of 1482. The difference is that Ramos urged the use of these proportions on the ground of expediency, saying that the older ones, i.e., 81:64 (major third) and 32:27 (minor third) were too laborious and difficult for singers to understand; the new ones, 5:4 and 6:5, were but simpler approximations. For Zarlino, the senario type of tuning was not a practical compromise because of the ignorance and inabilities of singers, but was a logical extension of the older system that once had been proposed by Ptolemy and then left in neglect; it thus had strong speculative roots and could provide a firm foundation on theoretical grounds as well as practical.
— Journal of the American Musicological Society, 23 (1970), 150-154.
|
From the Oeuvres Complètes (1661) of Christiaan Huygens:
It is established by experience, and those who have even the slightest ear for music cannot deny, that consonances in the above proportions [he has just given the just ratios] are very perfect and better than when one deviates from these true numerical proportions. And those who have dared to maintain the contrary and that the fifth does not consist in the ratio 3 to 2, either did not have an ear capable of judging it, or thought they had a reason for their opinion, but their conclusion was false.
Cited in D.P. Walker, “Seventeenth-Century Scientists’ Views on Intonation,” p. 113.
Original French:
Il est constant par l’experience, et ceux qui ont tant soit peu d’oreille pour la musique ne peuvent nier, que les consonances suivant les proportions susdites ne soient très parfaites et meilleures que quand on s’ecarte de ces veritable proportions numeriques. Et ceux qui ont osé soustenir le contraire et que la quinte ne consistast pas dans la raison de 3 a 2, ou n’avoient pas l’oreille capable d’en juger ou croioient avoir une raison pour cela, mais ils concluoient mal.
— Vol. XX, 32, 169.
Commentary on Huygens by D. P. Walker, in “Seventeenth-Century Scientists’ Views”:
Christiaan Huygens is, I think, unique in both tackling the problem [of the instability of true just intonation] and suggesting a plausible solution. He begins by denying Zarlino’s and Galilei’s assumption that unaccompanied singers use absolutely just intonation. He believes that they probably deviate more from just intonation than do tempered instruments. But, even if they did sing entirely just intervals, they would inevitably lose or gain pitch in the course of a song. In fact, says Huygens, one does often find that singers have risen or fallen by a semitone or more at the end of a piece. He suggests that the reason why a well-trained singer does not do this is because his memory is good enough to preserve the pitch of the original starting point. If you sing slowly this tune [see example below] and succeed in singing entirely just consonances, you will end up two commas flat ((81:80)²). But, if it is sung quickly, says Huygens, “je trouve que le souvenir de ce premier ut retient la voix dans le ton”, and that therefore some of the consonances must have been tempered (Oeuvres Complètes, XX, 76-7, 101).
Huygens example of a short melody that loses 2 syntonic commas if all the intervals are just:
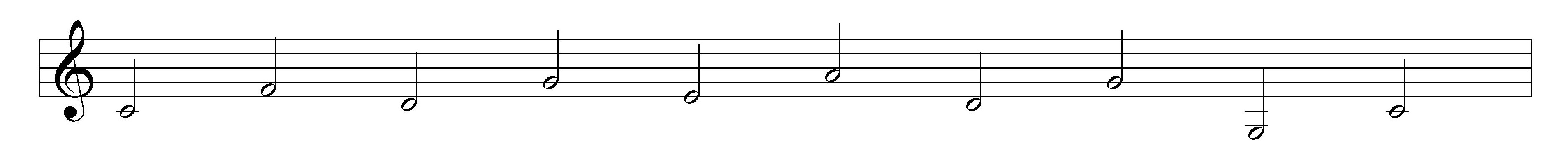
Demonstration:
C to F: 1/1 x 4/3 = 4/3
F to D: 4/3 x 5/6 = 20/18 = 10/9 [10/9 x 81/80 = 810/720 = 9/8] (first loss of a comma)
D to G: 10/9 x 4/3 = 40/27 [40/27 x 81/80 = 3240/2160 = 3/2]
G to E: 40/27 x 5/6 = 200/162 = 100/81 [3/2 x 5/6 = 15/12 = 5/4]
E to A: 100/81 x 4/3 = 400/243 [5/4 x 4/3 = 20/12 = 5/3]
A to D: 400/243 x 2/3 = 800/729 [5/3 x 2/3 = 10/9] (second loss of a comma)
D to G: 800/729 x 4/3 = 3200/2187
G to G: 3200/2187 x 1/2 = 3200/4374
G to C: 4374 x 4/3 = 12800/13122 = 6400/6561
80/81 x 80/81 = 6400/6561 (= 2 syntonic commas)
NOTE: The descent of a just minor third from a 4/3 F to D results in a 10/9 D instead of a 9/8 one, thus the loss of one syntonic comma.
Likewise the descent of a perfect fifth from a just 5/3 A results in a 10/9 D instead of a 9/8 one, thus the loss of another syntonic comma.
|