ACCIDENTAL NECESSITY AND POWER OVER THE PAST
Pacific Philosophical Quarterly
63 (1982): 54-68.
Alfred J. Freddoso
University of Notre Dame
The thesis of this paper is that an agent S has
the power to bring it about that a proposition p is or will be true
at a moment t only if S has at the same time the power to
bring it about that it has always been the case that p would be
true at t. The author first constructs a prima facie compelling
argument for logical determinism and then argues that whoever accepts an
Ockhamistic response to that argument should also accept the above thesis.
Some philosophers have recently defended what is commonly regarded as
a startling and even obviously false claim, viz. that it is at least conceivable
that some agent have the power to bring about the past.1
But this claim is actually much too modest, since, as I hope to show, we
have the sort of power that we ordinarily attribute to ourselves only if
we in fact have power over the past as well. More precisely, the thesis
I wish to defend is that an agent S has the power to bring it about
that a proposition p is or will be true at a moment t only
if S has at the same time the power to bring it about that it has
always been the case that p would be true at t. One noteworthy
corollary of this thesis is that the power to bring about the past is so
commonplace that such power would be relatively uninteresting if it were
not so frequently claimed to be impossible.
Since the sort of power I have in mind is rather mundane, this paper
will not include any discussion of such exotic items as time travel, deviant
notions of causality, or precognitive beings whose present actions are
influenced by what they know other agents will do in the future. Instead,
I will set the stage for my main argument by examining in some detail the
familiar but often misunderstood claim that the past is unalterable. This
will lead to a brief examination of a prima facie compelling argument for
logical determinism and of what I take to be the only three interesting
lines of response to that argument. Then I will argue that anyone who accepts
the Ockhamistic line of response, which in my view is the most attractive,
should also accept the thesis that we have power over the past.
I
It is by no means a simple task to capture in a general formula our
intuitions about the unalterability of the past. Consider the following
principle, which has appeared in the philosophical literature:2
/55/
(A) No one has the power at any moment t to do
anything such that were he to do it, what is at t a fact about the
past would at some time after t no longer be a fact about the past.
(A) is initially attractive. For instance, it is reasonable to believe
that since it is now a fact about the past that Caesar crossed the Rubicon,
no one now has the power to bring it about that tomorrow it will no longer
be a fact about the past that Caesar crossed the Rubicon. But while few
would challenge this example, (A) has other consequences which are less
benign. Suppose, for instance, that it is now true that David has never
been to Chicago. This is clearly a fact about the past. Now no one would
object to the further prosaic assumption that David now has the power to
do something (e.g., board an airplane) which will result in his being in
Chicago two hours from now. Yet (A) renders this assumption impossible.
For if David were now to exercise the power in question, then two hours
from now it would no longer be a fact about the past that David has never
been to Chicago.
So (A) is unacceptable as it stands. But at this point it would be natural
to suggest the following modification:
(A*) No one has the power at any moment t to do
anything such that were he to do it, what was a fact at an earlier moment
t* would not have been a fact at t*.
(A*) seems invulnerable to the above counterexample. If it was a fact
yesterday that David had never been to Chicago, no one can now bring it
about that it was not a fact yesterday that David had never been to Chicago.
However, (A*) is ambiguous. On one reading, it is simply a consequence
of the more general thesis that no agent has the power to make both a proposition
and its negation true at the same moment. So no one can have the power
at a moment t to bring it about that what was true at an earlier
moment t* was also not true at t*. While (A*) is undoubtedly true
on this reading, it does not give us what we were looking for, viz. a general
principle which captures the asymmetry between our control over the past
and our control over the future. For it is equally true, as many have pointed
out, that no one can have the power at t to bring it about that
what will be true at a later moment t* will also not be true at
t*. So on this first reading, (A*) is true but not to the point.
However, the second--and, I take it, the more natural--reading is more
interesting. Consider the following proposition:
If we let "P" stand for the past-tense propositional
operator, then (1) is logically equivalent to
On the second reading, (A*) presupposes that if (2) is now true, then
it can no longer be false. That is, if (2) is true now, then it is also
in some sense necessary now as well. Consequently, an agent S
can now have the power to make the negation of (2) true, i.e., to make
it true that Caesar never crossed the Rubicon, only if S can also
bring it about that at some past moment both the proposition Caesar
is crossing the Rubicon and its negation were true. So some true logically
contingent propositions (e.g., (2)) are such that their negations not only
are not /56/ in fact true now, but cannot be true now. But now consider
the following proposition:
If we let "F" stand for the future-tense propositional
operator, then (3) is logically equivalent to
Suppose that (4) is now true. It does not follow from (A*), on the second
reading, that (4) now has the same modal status as (2). Nor does there
seem to be any other plausible general principle from which this would
follow. (4) is, after all, a fact about the future and not about the past.
Hence, at least prima facie it seems that (A*) is consistent with the claim
that even though (4) is now true, it is not now necessary in the way in
which (2) is. And so it appears that on the second reading, (A*) does indeed
point to the asymmetry we were trying to capture. So (A*), taken on this
second reading, is the principle we were looking for--or so, at least,
it seems. (When I refer to (A*) hereafter, I will, unless otherwise indicated,
have the second reading in mind.)
Nevertheless, there are, I will argue, weighty reasons for rejecting
(A*). For (A*) is a consequence of and is epistemically supported by a
principle which is arguably the weakest link in a prima facie compelling
argument for logical determinism. And once we reject this principle, we
open the door to a strong positive argument for the conclusion that we
do indeed have power over the past.
(A*) is unduly inexplicit about the sort of necessity which now attaches
to (2) in virtue of its being a fact about the past. The necessity in question
is clearly not logical (i.e., metaphysical), physical or causal necessity.3
Rather, it is a necessity which, to put it crudely, is had by the past
simply because it is the past. Medieval logicians called this modality
necessity per accidens, i.e., accidental necessity. By investigating
accidental necessity in some detail, we will be able to come to a deeper
understanding of the issues involved in the question of whether we have
power over the past.
I will begin by fashioning a framework within which we can talk precisely
about the necessity of the past. First, I will make the simplifying (in
this context) assumption that all propositions are tensed. Though this
assumption seems to me both natural and true, it may not be absolutely
crucial. But I will leave it to the friends of "tenseless" propositions
to reconstruct what I will say in their own idiom. The assumption in question
has two relevant consequences. The first is that some propositions can
be true at some times and false at others. Examples are the present-tense
proposition David is in Chicago and the past-tense proposition Socrates
drank hemlock. Again, the future-tense proposition Socrates will
meet with Plato might be true now even though it will be false after
Socrates and Plato have met for the last time. The second consequence is
that some present-tense propositions can be true at at most one moment.
Examples are the propositions David is in Chicago at T and T
is present (or: it is (now) T), where T is a single determinate
moment of time. Each of these propositions can be true only at T.
/57/
I will now mention a few of the basic properties of accidental or per
accidens modality. First, since a proposition which is necessary per
accidens is, as the name suggests, such that its being necessary is
an accidental feature of it, only logically contingent propositions can
be necessary per accidens. An analogous point holds for the mode
of accidental impossibility. So in this regard per accidens modality
resembles physical and causal modality.
Second, a proposition's being necessary per accidens is, as should
be expected, relative to a time. For a proposition can--and typically does--become
necessary per accidens after not having been necessary. For instance,
the past-tense proposition Socrates drank hemlock is now (presumably)
necessary per accidens and thus can no longer be false. But it was
false when Socrates was a child. Again, an analogous point holds for accidental
impossibility.
From these first two points it follows that for any moment t,
logically contingent propositions may be divided into three mutually exclusive
and jointly exhaustive groups: (a) those which are necessary per accidens
at t; (b) those which are impossible per accidens at t; and
(c) those which are neither necessary per accidens at t nor
impossible per accidens at t. I will say that the members
of this third group are "temporally contingent" at t.
Third, a proposition's being necessary (impossible) per accidens
at a given moment entails that it remains necessary (impossible) per
accidens at every succeeding moment. This, again, is what we should
expect to be true of the necessity of the past. Also, since it appears
to be logically possible for a proposition to be physically necessary (or
a law of nature) at one moment and not at some later moment, this feature
of accidental necessity distinguishes it from both physical and causal
necessity. So some logically contingent propositions, e.g. (presumably),
Socrates drank hemlock, are not now and never will be possibly false,
and their negations are not now and never will be possibly true, where
the impossibility in question is accidental impossibility. Moreover, from
this it follows that if p is necessary per accidens at t,
then no one has the power at or after t to bring it about that p
is or will be false. And it also follows that if p is impossible
per accidens at t, then no one has the power at or after t to
bring it about that p is or will be true. In short, the necessity
of the past entails its unalterability. So the contention that no one can
ever have the power to alter a fact about the past is acceptable only if
we are careful to interpret it as follows: no proposition which is now
necessary per accidens is now or ever will be such that some agent
has the power to make it false, and no proposition which is now impossible
per accidens is now or ever will be such that some agent has the
power to make it true. And this is so even if the agent in question is
omnipotent.4
Fourth, when we limit the consequents to logically contingent propositions,
accidental necessity, like other kinds of necessity, is closed under entailment.5
That is,
(B) If p entails q, and q is logically
contingent, and p is necessary per accidens at t,
then q is necessary per accidens at t.
Further, given what was said in the preceding paragraph, it should be
clear that the conjunction of (B) with the obvious truth that no one has
the power to make a logically necessary proposition false entails /58/
(C) If p entails q, and p is necessary
per accidens at t, then no one has the power at or after t to
bring it about that q is or will be false.
(C), it should be evident, is beyond dispute. If p cannot be
false at or after t, then no proposition entailed by p can
be false at or after t--and so no one has the power at or after
t to make such a proposition false. Likewise, it is easy to show
that if p is impossible per accidens at t, then no proposition
which entails p can be true at or after t--and no one has
the power at or after t to make such a proposition true.
We now have a general framework for discussing the necessity of the
past. The obvious next step is to address the substantive question: just
which propositions are necessary or impossible per accidens at a
given moment? Let "P" and "F" stand,
as before, for tense operators, and let "N" stand for
the negation operator. Philosophers from Aristotle in ancient times to
Arthur Prior in our own century have, at least implicitly, accepted the
following principle:
(D) If p is true at t, then Pp
is necessary per accidens at every moment after t, and NPp
is impossible per accidens at every moment after t.
Once a proposition p has been true, it is always necessarily
true afterwards that p was once true. And once p has been
true, it is always necessarily false afterwards that p has never
been true. So not only is it the case that it will never in fact be false
after t that p was true, but it is also the case that it cannot
be false after t that p was true. According to the proponent
of (D), this amounts to saying, in possible worlds jargon, that in every
possible world just like ours up to and including t, it is true
at every moment after t that p was true. So, given (D), the
thesis that the past is necessary can be stated as follows: for any proposition
p, if it is now the case that p has been true, then it is
also necessary per accidens that p has been true; and if
it is now not the case that p has never been true, then it is also
impossible per accidens that p has never been true.
A moment's reflection reveals that (D) has (A*) as a direct consequence.
For (A*) in effect tells us that once a proposition p has been true,
then no one has the power to bring it about that p was never true.
Moreover, (D) provides epistemic grounds for accepting (A*), since it explains
our lack of power over the past by reference to the necessity of the past.
If (D) turned out to be false, it is not clear just what reason we would
have for accepting (A*) in all its generality.
Given the popularity enjoyed by (D), it is hard to deny its intuitive
appeal. At the very least, there is no obvious alternative on the horizon.
However, the disturbing fact is that (C) and (D) provide us with all we
need to construct the strongest (and, to my mind, the clearest) possible
argument for logical determinism. Let "T" designate some determinate
moment of time. The argument can then be formulated as follows:
(P1) F (David is in Chicago at T) is true
now, long before T. (assumption)
(P2) So PF (David is in Chicago
at T) will be necessary per accidens at every future moment,
including every future moment which precedes or is identical with T.
(from P1 and (D))
(P3) But PF (David is in
Chicago at T) entails If T is present, then David is in Chicago.
(assumption) /59/
(P4) Therefore, no one (including David) will have the
power at or before T to bring it about that If T is present,
then David is in Chicago is or will be false. That is, no one will
have the power at or before T to make it true that David is not
in Chicago when T is present. (from (P2), (P3) and (C)).
Given (D), the move from (P1) to (P2) is straightforward. Moreover,
(P3) simply reflects the normal belief that if it has ever been the case
that p will be true at a moment t, then either p has
already been true at t, or p is now true (at t), or
p will be true at t--depending on whether t is now
in our past, our present or our future. In short, if it has ever been the
case that p will be true at t, then p is true whenever
t is present. But if this is so, then, given (C) , the necessity
of the proposition PF (David is in Chicago at T) entails our inability
to affect the present and future truth-values of the proposition When
T is present, David is in Chicago.
So (C) and (D) enable us to reason validly from the unremarkable assumption
that it is now the case that David will be in Chicago at T to the outrageous
conclusion that no one will ever have the power to prevent David's being
in Chicago at T. (Notice that this is so whether the notion of power is
given a libertarian or a compatibilist construal.) Further, the argument
is not only valid but perfectly general, since similar deterministic consequences
follow whenever we substitute for the proposition F (David is in Chicago
at T) any other future-tense proposition whose present-tense counterpart
can be true at at most one moment.
Solutions to this argument fall into three main groups. "Aristotelian"
solutions all make the drastic move of denying the assumption (P1), claiming
either (a) that where p is a future contingent, both p and
its negation are neither true nor false; or (b) that where p is
contingent, it is false both that p will be true and that its negation
will be true, i.e., both Fp and FNp are false. The first
of these claims is commonly attributed to Aristotle, while Prior is responsible
for the second.6
A second type of solution, at least suggested by some remarks made by
Peter Geach, consists in rejecting the assumption (P3) in favor of the
rather startling claim that future-tense propositions express only present
intentions, dispositions and tendencies.7 So, for instance,
even though it might have been true on Monday that David would be in Chicago
on Tuesday, it could still be true that David is never in Chicago on Tuesday.
For on Monday he may have intended to be in Chicago on Tuesday, but then
changed his mind.
"Ockhamistic" solutions, on the other hand, all deny the inference
from (P1) to (P2) on the ground that (D), despite its initial attractiveness,
is a needlessly and unacceptably strong interpretation of our pre-theoretic
beliefs about the necessity of the past. For, according to the Ockhamist,
when p is a future-tense proposition true before t, it simply
does not follow that in every possible world just like ours prior to t,
Pp is true at t and at every moment after t. The most
pressing task facing the Ockhamist is to explicate the notion of two worlds
being just like one another prior to a given moment in a way which (a)
is strong enough to render plausible the claim that two such worlds share
the same history at the moment in question and (b) is weak enough not to
lead to deterministic consequences when combined with assumptions like
(P1) and (P3). This turns out to be a very difficult and complicated task.
Roughly speaking, the Ockhamist's /60/ strategy is to find a plausible
way to distinguish the propositions which are "presently" true
at a given moment t from the past-tense and future-tense propositions
true at t. The latter, he holds, are true at t only in virtue
of what was "presently" true at moments before t or what
will be "presently" true at moments after t. He then substitutes
for (D) the weaker claim that a proposition p is necessary per
accidens at t just in case p is a logically contingent
proposition which is true at every moment at and after t in every
possible word which shares all of our world's "presents" prior
to t. This invalidates the move from (P1) to (P2), since in some
possible world which shares all of our world's "presents" up
to and including the present moment, David is not in Chicago at the time
in question. So in that world the proposition PF (David is in Chicago
at T) is never true, from which it follows that this proposition, though
true before T in our world, is never necessary per accidens
before T in our world.
In short, the Ockhamist holds that since the present-tense proposition
David is in Chicago at T has not yet been true, the past-tense proposition
PF (David is in Chicago at T), though now true, does not count as
part of our history at the present moment. And, he insists, only someone
with implausibly inflated notions of actuality and history would think
otherwise. To put it very roughly, then, the Ockhamist contends that the
only past-tense propositions which do count as part of our history (and
hence are necessary per accidens) are those whose present-tense
counterparts have already been true. So he agrees, for instance, that no
one can now have the power to make it true that Caesar never crossed the
Rubicon. But a relevant corollary of his position is that no argument based
simply on the necessity of the past is sufficient to yield the conclusion
that if it has already been true that David will be in Chicago at T,
then no one can have before T the power to bring it about that the
proposition NF (David is in Chicago at T) has been true at every
past moment. So in rejecting (D), the Ockhamist casts a shadow of doubt
on (A*) as well.
In another place I have defended in some detail an Ockhamistic theory
which, I believe, successfully solves the problems that have plagued its
historical ancestors.8 However, here I will be content
to argue for the conditional thesis that if an Ockhamistic response to
the argument for logical determinism is correct, then we in fact have power
over the past. Nevertheless, the discussion of logical determinism has
strengthened my dialectical position. For of the three types of responses
mentioned above, only the Ockhamistic response is compatible with each
of the commonly accepted theses (a) that if p is or will be true,
then Fp has been true at every past moment, and (b) that if t
is present and t is prior to t* and F(p-at-t*)
has ever been true, then p will be true at t*. In what follows
I will argue that anyone who accepts these theses while rejecting logical
determinism is committed to the claim that we have power over the past.
So if my argument is successful, then one can deny that we have power over
the past only by embracing either logical determinism or one of the first
two lines of response described above. My suspicion is that many who are
antecedently inclined to deny that we have any power over the past will
find each of these alternatives highly implausible. In fact, it is worth
noting that no one who espouses causal determinism, whether of the hard
or soft variety, can accept either of the first two lines of response mentioned
above, since both presuppose that the truth-values /61/ of some future-tense
propositions are not now fixed in the way demanded by a thoroughgoing causal
determinism. In short, in order to avoid being a logical determinist, a
causal determinist has no choice but to accept the Ockhamistic position.
So causal determinists constitute a subset---but only a proper subset--of
the set of those at whom the following argument is aimed.
II
It is important to notice that the Ockhamist position does not by itself
entail the negation of (A*) or the concomitant thesis that we do in fact
have at least some power over the past. In fact, it might appear that the
Ockhamist's most prudent strategy is simply to withhold judgment on (A*).
However, I will now argue that this appearance is deceptive.
Let K be a linearly ordered set, the set of times. And let T
and T* be two members of K such that (a) T >
T*, i.e., T* is prior to T, and (b) for some t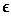 K,
T* > t, i.e., T* is not the first moment of time.9
Further, let "now" be a non-rigid designator indicating the
present moment relative to an assignment of truth-values. For instance,
given the Ockhamistic position, the future-tense proposition F (David
is in Chicago) is true just in case for some t K,
T* > t, i.e., T* is not the first moment of time.9
Further, let "now" be a non-rigid designator indicating the
present moment relative to an assignment of truth-values. For instance,
given the Ockhamistic position, the future-tense proposition F (David
is in Chicago) is true just in case for some t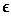 K,
t > now and David is in Chicago will be true at
t. Now consider the following propositions: K,
t > now and David is in Chicago will be true at
t. Now consider the following propositions:
(5) David is in Chicago will be true at T,
and
(6) F (David is in Chicago at T)
was true at every moment prior to T* .
In what follows I will support the claim that we have power over the
past by arguing that if an agent S has the power at T* to
bring it about that David is in Chicago will be true at T, then
S also has the power at T* to bring it about that the future-tense
proposition F(David is in Chicago at T) was true at every moment
before T*. That is, I will argue that the following conditional
proposition is true, where "S" ranges over human agents:
(7) If S has the power at T* to make (5)
true at T*, then S has power at T* to make (6) true
at T*.
My argument will be generalizable in obvious ways to other propositions
and to other pairs of times meeting the two conditions (a) and (b) imposed
above on T and T*.
If the Ockhamist is correct, then (6) is temporally contingent at T*,
since its truth-value at T* depends on what will be "presently"
true at a future moment, viz. T. So, to corroborate a point made
above, no Ockhamist can reject (7) on the ground that (6) is either necessary
or impossible per accidens at T* and hence such that no one can
affect its truth-value at or after T*. Further, I am assuming that
any Ockhamist is willing to concede that someone might have the power at
T* to make (5) true at T*.10 Of course,
this concession entails the claim that the proposition F (David is in
Chicago at T) might be true before T. But unlike the Aristotelians,
the Ockhamist considers this claim wholly acceptable and perhaps even self-evident.
For it follows directly from the first of the two theses alluded to near
the end of section I, viz. /62/
(E) If p is or will be true, then Fp
has been true at every past moment.
Now it is reasonable to believe that having the power to make (5) true
at T* is equivalent to having the power to make the following conjunctive
proposition true at T*:
(8) T* = now, and David is in Chicago
will be true at T
That is, having the power to make (8) true is tantamount to having the
power to make (5) true while T* is present. Nevertheless, someone
might object to this claim as follows: "No human agent ever has the
power to bring it about that a given moment is present. That is, moments
become present or past completely independently of anything we do or can
do. But the following principle is obvious:
(F) If S has the power to make p and q true
at t, then (i) S has the power to make p true at t and
(ii) S has the power to make q true at t.
However, given (F), no agent has the power to make (8) true at T* unless
he also has the power to make the proposition T* = now true at T*.
Since no agent has this latter power, no agent can make (8) true at T*.
Though (F) is not self-evidently false, this very example should make
us suspicious. Moreover, other examples are even more striking. For instance,
it seems eminently reasonable to suppose that David, never having been
to Chicago, might have the power at T* to make it true that he will
someday be in Chicago for the first time. However, if (F) is true, then
he cannot have such power. For the supposition in question entails that
David has the power at T* to make the following conjunctive proposition
true:
(9) David is in Chicago was false at every moment
before T*, and David is in Chicago will be true at some moment
after T* .
But even the Ockhamist believes that the first conjunct of (9) is necessary
per accidens at T* and, hence, that no one has the ability
at T* to affect its truth-value. So even power as ordinary as that
in question here is ruled out by (F). Again, even a power as commonplace
as, say, the power to paint a wooden chair black involves the ability to
make certain bodily movements while a given set of physical laws
hold, e.g., laws of gravity, laws governing the adhesion of paint to wooden
surfaces, etc. So, it seems, to attribute to an agent even so unremarkable
a power is to attribute to that agent the power to bring about a complex
state of affairs, many of the components of which (e.g., physical laws)
are beyond his power to bring about. All of this suggests that we should
reject (F) in favor of some version of what Roderick Chisholm calls the
"principle of the diffusiveness of power.''11
For present purposes we need only a very weak version of this principle,
viz.
(G) If (i) S has the power to make p true
at t and (ii) q is or will be true at t and (iii)
no agent has ever had or ever will have the power to make q false
at t, then S has the power to make p and q true at
t.
Given (G) , it follows that someone who has the power to make
true at T* also has the power to make /63/
(8) T* = now, and David is in Chicago will
be true at T
true at T*. For no one has ever had or ever will have the power to bring
it about that the proposition T* = now is false at T*.
Moreover, we can explain the intuitive appeal of (F) by pointing out
that a principle like (F) is a plausible constraint on any account of just
which actions are "basic" for an agent at a given time, where
basic actions, in Chisholm's words, "are things we succeed in doing
without undertaking still other things to get them done." 12
For if S has the power to make p and q true at t as
a basic action,, then it is reasonable to think that S must have
the power to make p true at t and also the power to make
q true at t. Furthermore, even if (F) is false, the following
weaker principle is clearly acceptable:
(H) If S has the power to make p and q true
at t, then either (i) S has the power to make p true
at t or (ii) S has the power to make q true at t.
It is difficult to imagine what a genuine counterexample to (H) would
even look like.13
Now it might appear at this point that the denouement is at hand. For,
as we have seen, whoever has the power at T* to make (5) true at
T* also has the power at T* to make (8) true at T*.
But given the Ockhamistic thesis (E) noted above, (8) entails
And the following principle seems highly plausible:
(I) If (i) p entails q and (ii) S has
the power to make p true at t, then S has the power
to make q true at t.
So whoever can make (8) true at T* can also make (6) true at
T*. And by the transitivity of implication it follows that whoever
has the power to make (5) true at T* also has the power to make
(6) true at T* . In short, (7) is true.
Unfortunately, this argument will not work. For, as Joshua Hoffman and
Gary Rosenkrantz have recently shown, (I), unlike close analogues for the
modes of logical necessity and possibility, is false--even when we limit
the range of p and q to logically contingent propositions.14
To put it succinctly, power is not closed under entailment. For instance,
the proposition Some rocket ship is red entails the proposition
There is a rocket ship. But, obviously, an agent might have the
ability to paint a rocket ship red without having the technical expertise
required to bring a rocket ship into existence. So (I) is false, and we
must look elsewhere for a defense of (7).
Luckily, help is not far off. Even though (8) is not logically equivalent
to (6), it is logically equivalent to the following close relative of (6):
(10) T* = now, and F (David
is in Chicago at T) was true at every moment prior
to T* .
The inference from (8) to (10) is, as above, sanctioned by the Ockhamistic
thesis (E). And the inference from (10) to (8) is sanctioned by the second
of the two theses noted near the end of section I:
(J) If (i) t = now and (ii) t* > t
and (iii) F(p-at-t*) was true at some moment before t,
then p will be true at t*. /64/
So (8) and (10) are logically equivalent. But the following principle,
unlike its cousin (I), is impeccable:
(K) If (i) p is logically equivalent to q and
(ii) S has the power to make p true at t, then S has
the power to make q true at t.
Thus, whoever has the power to make (8) true at T* also has the
power to make (10) true at T*.15
We now have all we need to construct a valid deductive argument for
(7). Suppose that the antecedent of (7) is true. That is, suppose that
S has the power at T* to make
true at T*.
Then it follows from (G) that S also has the power at T*
to make
(8) T* = now, and David is in Chicago will
be true at T
true at T*. But by the Ockhamistic theses (E) and (J), (8) is logically
equivalent to
(10) T* = now, and F (David
is in Chicago at T) was true at every moment prior
to T* .
So, by (K), S has the power at T* to make (10) true at
T* . But S does not, as we have seen, have the power at T*
to make the first conjunct of (10) true at T*. No one has such power. So
it follows from (H) that S has the power at T* to make the
second conjunct of (10) true at T*. But the second conjunct of (10)
is identical with
So S has the power at T* to make (6) true at T*. Thus,
if S has the power at T* to make (5) true at T*, then S
has the power at T* to make (6) true at T*. Hence, (7) is true.
And anyone who concedes that the antecedent of (7) can be true must also
admit that S can have the power at T* to bring it about that
the future-tense proposition F (David is in Chicago at T) was true
at every moment before T*.
Notice that this argument depends only on the Ockhamistic theses (E)
and (J) and on the principles (G), (H) and (K). Moreover, while (H) and
(K) hardly require an argument, I have given what I take to be solid reasons
for favoring (G) over its competitor (F) . So at the very least I have
shown that it is reasonable for an Ockahamist to hold that we have power
over the past, i.e., over certain temporally contingent past-tense propositions.
And in the absence of good independent arguments against (G) , (H) or (K),
I am prepared to say that my argument makes it epistemically obligatory
for Ockhamists to accept (7) and the innumerable propositions that could
be substituted for it.
Of course, the power over the past which I have argued for is rather
limited, since an agent can have the power at t to make a given
past-tense proposition true (or false) only if that proposition is neither
necessary per accidens nor impossible per accidens at t.
But Ockhamists all agree that there are many past-tense propositions that
are contingent in this sense. At the risk of glossing over the differences
which separate Ockhamists from one another, we can say simply that a past-tense
proposition is contingent in the sense in question if its present-tense
/65/ counterpart has not yet been true. (In what follows I will elaborate
a bit on this.) On the other hand, the philosophers alluded to at the very
beginning of this paper are far more liberal than the average Ockhamist
in their claims about such contingency. They might insist, for example,
that it is at least conceivable that someone now be transported to Socrates'
death scene and find himself in a position to prevent Socrates from drinking
the hemlock. Such power over the past obviously goes far beyond anything
I have claimed here, and in this sense my argument is less interesting
than their arguments are. However, I hope that it is clear that my position
is also much more plausible than theirs, since it does not depend upon
further dubious metaphysical presuppositions, e.g., that there can be two
independent time dimensions, or that a person is literally a mereological
sum of temporal parts, two of which might confront each other in a time
travel scenario, etc. Instead, each of the assumptions I have employed
seems to have substantial intuitive weight.
To summarize, then, anyone who accepts the Ockhamistic response to logical
determinism can reject (7) only at the cost of having to give up (G), (H)
or (K) . This is, at best, an uncomfortable choice.
III
I will now consider two fairly obvious objections to what has been said
above:
(a) "Your view entails that contradictory propositions can be true
at the same time. For suppose that David will not be in Chicago at T,
even though he now (at T*) has the power to make it true that he
will be in Chicago at T. In that case, the future-tense proposition
NF(David is in Chicago at T) has been true at every moment before
T* . But according to you, David now has the power to bring it about
that F (David is in Chicago at T) was true at every moment before
T*. Now suppose that David were to exercise this power. Then it
would be the case that F (David is in Chicago at T) was true at
every moment before T* . But, as we have just seen, it would also
be the case that NF (David is in Chicago at T) was true at every
moment before T* . It follows that contradictories will have been
true at every past moment."
This conclusion does not follow. For just as p and possibly q
can be true even though p and q is impossible, so too p and someone
has the power to make q true can be true even though p and q is
impossible. The fact that NF (David is in Chicago at T) has been
true at every moment before T* entails only the no one will in
fact make it the case that its negation was true at every moment before
T* . It does not entail that no one has the power to do so. To say
that David has the power at T* to make it the case that F (David
is in Chicago at T) was true at every moment before T* implies
only that there is a possible world w which shares the same history
with our world at T* and is such that at T* in w David
exercises this power. And, as I suggested above, the Ockhamistic position
can be summed up in the claim that a careful explication of the phrase
"shares the same history with our world at T*" reveals
that it is plausible to suppose that there is such a world--even if David
does not exercise the power in question at T* in our world. Of course,
if he exercises this power at T* in w, then the /66/ proposition
NF (David is in Chicago at T) is never true before T* in
w. So my view does not entail that there is a moment--either in
our world or in w--at which both of the contradictory propositions
in question are true.
Nor does my view entail that David can alter the past, if we mean by
this that he can bring it about that F (David is in Chicago at T) has
always been true and that its negation has also always been true. That
is, my view does not contravene (A*) above when it is construed according
to its first reading. However, if we mean only that while NF (David
is in Chicago at T) has in fact always been true before T*,
its negation is such that David has the power to bring it about that it
was always true before T*, then my view does entail that David has
the power to alter the past. For this is just to say that PNF (David
is in Chicago at T), while true at T*, is not necessary per
accidens (i.e., part of our history) at T* . So my view
entails, unsurprisingly, that (D), along with the second reading of (A*),
is false. We might say that the Ockhamist holds that our past, but
not our history, can be altered. Still, it is probably misleading
to use the phrase "alter the past" in this sense, and so I am
prepared to jettison it in favor of the more accurate locutions employed
above.
(b) "Your view has the odd consequence that an agent can have the
power to make a proposition true even though that proposition is already
true. For suppose that David has the power at T* to bring it about
that F (David is in Chicago) will be true at T. And suppose
further that he exercises this power at T*, so that the proposition
David is in Chicago is true when T is present. From this it follows
that the proposition F (David is in Chicago at T) was always true
before T* . Yet on your view David has the power at T* to
"bring it about" or "make it true" that this proposition
has always been true before T* . How can this be?"
Note, first, that my position is not the only one confronted by this
difficulty. For instance, according to the "timeless" theory
of truth every true proposition is eternally true and every false proposition
is eternally false. So the "tenseless" proposition Jones is
in class at T is, if true, true at every moment, including every moment
before T. Yet one who holds such a view would presumably want to
admit that Jones might have the power at T* to bring it about that
Jones is in class at T is true, and hence eternally true.
Ockhamists, at least, have the resources to show that there really is
no problem here. For, as I suggested above, they hold that the truth-value
of any past-tense or future-tense proposition at a given time depends on
the past or future truth-values of relevant present-tense propositions.
For instance, the present truth-value of the proposition F (David is
in Chicago at T) depends on whether the present-tense proposition David
is in Chicago at T will be true at T. Moreover, the dependence
in question is asymmetric. The present-tense propositions true at a given
moment determine, according to this view, what is "presently"
true at that moment, whereas the past- and future-tense propositions true
at that moment do not. Instead, they depend on what was (will be) "presently"
true at some past (future) moment or moments.
This notion of temporal dependence must, of course, be fleshed out more
precisely, and I have attempted to do this elsewhere.16
But while the articulation of this notion is rather complicated, the intuition
which underlies it is rather /67/ straightforward and attractive. Undergraduates,
when first confronted with an argument for logical (or theological) determinism
based on the necessity of the past, frequently respond that it is now true
(or: God now knows) that David will be in Chicago at T because it
will be the case at T that David is in Chicago. But the converse
does not hold. That is, the following is thought to be clearly false: it
will be true at T that David is in Chicago because it is
now true (or: God now knows) that David will be in Chicago at T.
Confusion is generated by the fact that these occurrences of the term "because"
are often taken to signal causal dependence. But this construal does not
do justice to the intuition in question, which has to do with logical (in
a broad sense) rather than causal dependence.
Once we grant the validity of this intuition, we can then go on to say
that at T* David brings it about that the proposition F (David
is in Chicago at T) has always been true before T* by bringing
it about that the proposition David is in Chicago will be true at
T. And we can deny that David brings it about that David is in Chicago
will be true at T by bringing it about that F (David is in Chicago
at T) has always been true before T*. That is, anyone who brings
it about that a future-tense proposition has always been true does so by
bringing it about that an appropriate present-tense proposition is or will
be true. So power over the past is not basic, but is rather parasitic on
ordinary causal contribution to what occurs "presently." Of course,
the proposition F (David is in Chicago at T) has always been true
at the moment when David brings it about that it has always been true.
But, as just noted, its past and present truth depend upon the future truth
of the present-tense proposition David is in Chicago. Any possible
world sharing the same history with ours at T* in which David
is in Chicago is false at T is by that very fact a world in
which F (David is in Chicago at T) is never true. So there is a
perfectly straightforward sense in which David has the power at T*
to bring it about that F (David is in Chicago at T) has always been
true even though this proposition is already true. For its truth depends
upon the future truth of the present-tense proposition David is in Chicago,
and at T* David has the power to bring it about that this present-tense
proposition will be true at T.
So my view may appear initially to have an odd consequence, but this
appearance is illusory. What would be genuinely odd--and perhaps this is
the underlying intuition on which objection (b) is based--is the claim
that one could have the power to make a present-tense proposition p
true at a time t when p would be true at t no
matter what any agent were to do. This is not only odd, but impossible.
In summary, then, we have seen that a systematic framework for talking
about the necessity of the past suggests a strong argument for logical
determinism, and that one who espouses an Ockhamistic response to this
argument can and should embrace the thesis that agents in fact have power--albeit
limited power--over the past. Though someone might be tempted to use this
result as an argument against the Ockhamistic position, I have tried to
show in the final section that Ockhamists can satisfactorily handle at
least the most obvious objections to the claim in question.17
/68/
NOTES
1. See, e.g., Michael Scriven, "Randomness and
the Causal Order," Analysis 17, 1957, 5-9; Michael Dummett,
"Bringing About the Past," Philosophical Review 73, 1964,
338-359; Larry Dwyer, "Time-Travel and Changing the Past," Philosophical
Studies 17, 1975, 341-350; and David Lewis, "The Paradoxes of
Time-Travel," American Philosophical Quarterly 13, 1976, 145-152.
2. For example, William Rowe, in Philosophy of Religion:
An Introduction (Encino, Calif., 1978), 154-169, and "On Divine
Foreknowledge and Human Freedom: A Reply," Philosophical Studies
37, 1980, 429-430, puts into the mouth of the theological determinist a
principle much like (A).
3. I am interpreting physical necessity and causal necessity
in the following ways: p is physically necessary just in case it
is a law of nature; and p is causally necessary at t just
in case for some q (relevant causal conditions), q is true
at t and it is physically, but not logically, necessary that if
q is true, p is true.
4. Although I am primarily interested in unalterability
here, it should also be noted for future reference that once a proposition
becomes necessary per accidens, no one has the power to bring it
about that it is or will be true, and once a proposition becomes impossible
per accidens, no one has the power to bring it about that it is or will
be false. So in this regard per accidens necessity and impossibility
resemble logical necessity and impossibility. For a discussion of the role
of accidental necessity in the formulation of an adequate analysis of omnipotence,
see Thomas P. Flint and Alfred J. Freddoso, "Maximal
Power," in Alfred J. Freddoso (ed.), The Existence and Nature
of God (Notre Dame, forthcoming).
5. I will say that p entails q just in
case it is logically impossible that there be a moment at which p is
true and q is false. Similarly, p is logically equivalent
to q just in case it is logically impossible that there be a moment
at which p and q differ in truth-value.
6. See Aristotle, On Interpretation, chap. 11,
and A. N. Prior, Past, Present and Future (Oxford, 1967), 128-134.
7. See Peter T. Geach, Providence and Evil (Cambridge,
1977), 40-66.
8. See my "Accidental
Necessity and Logical Determinism."
9. Condition (b) simply ensures that there is a past
at any moment at which an agent will be claimed to have power over the
past.
10. The argument which follows would work just as well
on the alternative assumption that an agent might have the power at T*
to bring it about that (5) is or will be true at some t such that
T > t > T* . But this assumption would needlessly
complicate the argument, and so I have chosen to employ its simpler counterpart.
11. See Roderick M. Chisholm, Person and Object
(Lasalle, I11., 1976), 65.
12. Person and Object, 84.
13. I say "genuine" here, since spurious
counterexamples can easily be generated if (H) is given the following inaccurate
reading: if S has the power to bring it about that p and q is
true at t, then (i) S has the power to bring it about that
p and not-q is true at t or (ii) S has the power to bring
it about that q and not-p is true at t.
14. See "On Divine Foreknowledge and Human Freedom,"
Philosophical Studies 37, 1980, 289-296.
15. It is worth noting that (K) is incompatible with
(F) above, since any proposition p is logically equivalent to its
conjunction with a logically necessary truth. So, for instance, if (K)
is true, then whoever has the power to make p true at t also
has the power to make p and 2 + 2 = 4 true at t. But no one
can have the power to make 2 + 2 = 4 true. So anyone who accepts
(F) must reject (K) as well as (G). Given (K)'s intuitive appeal, this
result provides us with another strong reason for rejecting (F).
16. See my "Accidental
Necessity and Logical Determinism."
17. I wish to thank Thomas Flint, Richard Foley, Jorge
Garcia, Philip Quinn and an anonymous referee for their helpful comments
on earlier drafts of this paper.
|