Math 10350 Calculus A In-class Exercises

Which of the following is the graph of a function?

Solution: Going clockwise from top left: yes, no, no, yes.

A electronic company decides to set the sale price of a sound card at $\$60$ a piece for an order of 100 pieces. The sale price drops to $\$50$ a piece for an order of 200 pieces.

1. Assuming that the sale price for one sound card is a linear function of the size of the order, find a formula for the sale price s dollars per sound card in terms of the size x of the order. What is the revenue function from the sales of the sound card?
2. Suppose further that the company has a monthly overhead cost of $\$5000$ for producing the sound cards and a cost of $\$10$ for producing each piece of the sound card. What is the monthly profit from the sales of the sound card in terms of month production assuming that all items produced are sold?
3. What is the maximum profit the company can make and when does that happen?
4. Graph the monthly profit function labelling the axis of symmetry, vertical intercept and vertex.

Solution:

1. $s=-\frac{1}{10}x+70$.
2. $\textrm{profit} = -\frac{1}{10}x^2+60x-5000$.
3. Maximum is 4000 attained when $x=300$.
4. Convex down parabola with vertex at $(300,4000)$, vertical intercept $(0, -5000)$ and axis of symmetry $x=300$.

Rewrite each of the following quadratic functions in the form $A(x + B)^2 + C$:

1. $x^2 − 6x − 5$,
2. $−2x^2 − 8x + 1$.
3. Graph the quadratic function in (ii). State the coordinates of the vertex and the equation of the axis of symmetry.

Solution:

1. $(x-3)^2-14$.
2. $-2(x+2)^2+9$.
3. Vertex at $(-2,9)$, axis of symmetry $x=-2$.

Apply the Laws of Exponents below: \begin{align*} 3^{12}\cdot 3^{5}&=\\ 2^7\cdot 3^7&=\\ \frac{7^5}{7^9}&=\\ 23^0&=\\ 5^{1/7}&=\\ \left(\frac{2}{3}\right)^4&=\\ 1^{17}&=\\ \frac{1}{4^9}&=\\ (3^5)^4&=\\ 2^6\cdot 3^3&=\\ 0^0&= \end{align*}

Solution: \begin{align*} 3^{12}\cdot 3^{5}&=3^{17}\\ 2^7\cdot 3^7&=6^7\\ \frac{7^5}{7^9}&=7^{-4}\\ 23^0&=1\\ 5^{1/7}&=\sqrt[7]{5}\\ \left(\frac{2}{3}\right)^4&=\frac{2^4}{3^4}\\ 1^{17}&=1\\ \frac{1}{4^9}&=4^{-9}\\ (3^5)^4&=3^{20}\\ 2^6\cdot 3^3&=12^3\\ 0^0&=\textrm{nonsense} \end{align*}

Let $f(x) = \dfrac{x + 1}{x − 2}$ and $g(x) = \dfrac{2}{x + 1}$. Evaluate the following

1. $f(3/2)$
2. $f(g(a))$ simplifying your answer ($a\neq -1$)

Solution:

1. $f(3/2)=-5$
2. $f(g(a))=\dfrac{a+3}{-2a}$

Solve the following equations: \begin{align} 4^x&=\dfrac{1}{8}\\ 3\cdot 9^{x+1}&=81^x \end{align}

Solution:

1. $x=-3/2$
2. $x=3/2$

A quantity $y$ is said to grow or decay exponentially with time $t$ if $y(t) = k \cdot a^t$. It is known that the amount of a medication in a patient reduces from an initial amount of 100 mg to 40 mg after three hours.

1. Assuming that the amount of medication decays exponentially, write a formula for the amount of the medication $y(t)$ as a function of time $t$ in hours.
2. What is the half life of the medication in the body?
3. Draw a graph for $y(t)$.

Solution:

1. $y=100 \cdot \sqrt[3]{0.4}^t$
2. Half life is $t=\log_{\sqrt[3]{0.4}}0.5$.

Sketch the graph of the inverse of $a^x$, i.e., the function $\log_a x$, for $a > 1$. State its domain and range.

1. Change to log base b: $\log_a x =$
2. $\log_a(a)=$
3. $\log_a(1)=$
4. $\log_a(xy)=$
5. $\log_a(x^n)=$
6. $\log_a(\frac{x}{y})=$
7. $\log_a(a^x)=$
8. $a^{\log_a x}=$
9. $a^{x\log_a x}=$
10. $\ln(e^x)=$
11. $e^{\ln x}=$

Solution: Domain $(0,\infty)$, range $(-\infty,\infty)$.

1. Change to log base b: $\log_a x =\frac{\log_b x}{\log_b a}$
2. $\log_a(a)=1$
3. $\log_a(1)=0$
4. $\log_a(xy)=\log_a x+\log_a y$
5. $\log_a(x^n)=n \log_a x$
6. $\log_a(\frac{x}{y})=\log_a x-\log_ay$
7. $\log_a(a^x)=x$
8. $a^{\log_a x}=x$
9. $a^{x\log_a x}=x^x$
10. $\ln(e^x)=x$
11. $e^{\ln x}=x$

Solve the following equations:

1. $\log_2(2x + 3) = \log_2(x + 1) + 2$
2. $3(4^{x−1}) = 5$ (Give your answer in base e)
3. $4e^{x−2} = 3e^{2x}$

Solution:

1. $x=-1/2$
2. $x=1+\log_4(5/3)$
3. $x=\ln(4/3)-2$

Given that $\ln(x) = p$ and $\ln(y) = q$, write the following expressions in term of p and q:

1. $\ln(5x^2y^3)=$
2. $\ln\left(\sqrt[5]{\frac{e^4x}{y}}\right)=$

Solution:

1. $\ln(5x^2y^3)=5+2p+3q$
2. $\ln\left(\sqrt[5]{\frac{e^4x}{y}}\right)=(4+p-q)/5$

The half life of the coronavirus on glass is estimated to be about 14 hours.

1. Starting with 100% initially, find a formula in the form $A \cdot b^t$ for the percentage of the virus on glass after $t$ hours.
2. If we consider the virus no longer infectious (or viable) after it is reduced to 1% or less, estimate how long will the virus remain infectious on glass.

Solution:

1. $c(t)=(\sqrt[14]{0.5})^t$
2. $t=\ln(0.01)/\ln((\sqrt[14]{0.5})$

1. Write down a formula for the balance A for an investment with principal $\$1000$ earning interest at a rate of 5% compounded continuously after $t$ years.
2. Find the doubling time of the account in years and months (to the nearest integer). Does the doubling time depends on the principal?

Solution:

1. $A(t)=1000\cdot e^{0.05 t}$
2. $t=\ln(2)/0.05$, does not depend on principal

At what interest rate would an account double (resp. triple) in amount after 10 (resp. 20) years if interest is compounded monthly?

Solution: Solve $P\cdot(1+\frac{r}{12})^{12\cdot 20}=3P$ and get $r=12(3^{1/240}-1)$.

You take out a 30-year mortgage with 3.25% annual interest rate. You have to choose between compounding continuously or monthly. Assuming you do not have to make any payments for 1 year, which method should you choose and how big of a difference is there on a 300000 principal after 1 year?

Solution: Continuously the balance is $A_{\textrm{continuously}}(1) = 300000 e^{0.0325}\approx 309910$. Compounded monthly the balance is $A_{\textrm{monthly}}(1)=300000(1+\frac{0.0325}{12})^{12}\approx 309896$. Monthly is cheaper by 13.

Compute the limit, if it exists: \[\lim_{x\to 2}\frac{-2x^2+9}{\sqrt{x+2}}\]

Solution: Limit is $1/2$.

What is the limit \[\lim_{x\to 0^+}\sqrt[3]{\frac{x^{3/2}}{x^2+1}}\]

Solution: Limit is 0.

Consider the piecewise defined function \[f(x)=\begin{cases}2-x& -\infty \lt x\lt 0\\ x^2& 0\leq x\lt 1\\ 1& 1\leq x\lt \infty \end{cases}.\]

1. Compute the following limits and values if they exist without sketching the graph.
   1. $\displaystyle f(-1)$
   2. $\displaystyle f(3)$
   3. $\displaystyle \lim_{x\to 0^+}(2f(x)-5)$
   4. $\displaystyle \lim_{x\to 0}(f(x))^2$
   5. $\displaystyle \lim_{x\to -5}(f(x))^2$
2. Sketch the graph of $f(x)$.

Solution:

1. $\displaystyle f(-1)=3$
2. $\displaystyle f(3)=1$
3. $\displaystyle \lim_{x\to 0^+}(2f(x)-5)=-5$
4. $\displaystyle \lim_{x\to 0}(f(x))^2$ does not exist
5. $\displaystyle \lim_{x\to -5}(f(x))^2=49$

$f(x) =\dfrac{x − 3}{x^2 − x − 6}$.

1. What is the domain of $f(x)$?
2. What are the discontinuities of $f(x)$?
3. Draw the graph of $f(x)$

Solution:

Determine the constants a and b such that the following function is continuous on the entire real line \[f(x)=\begin{cases}2 & -\infty \lt x\leq -1\\ ax+b & 1\lt x\lt 3\\ -2 & 3\leq x\lt\infty \end{cases}.\]

Solution:

Water is flowing into a tank at a rate such that the volume $V(t)$ (in cubic feet) of water in the tank at time $t \geq 0$ (in minutes) is given by $V(t) = \sqrt{t+4}$. Answer the following questions:

1. Find the average rate of change of the volume of water over the time duration [5, 12]. What is the unit of your answer?
2. Using limits, find the rate of change of the volume of water at the fifth minute. What is the unit of your answer?

Solution:

Solve the equations: \begin{align} (2x-1)^2 &= 3(x-1)^2+33\\ 8(1+\frac{r}{5})^3&=27 \end{align}

Solution:

Simplify the expressions: \[\frac{x^2+7x+12}{x^2-x-12}\ \ \textrm{and}\ \ \frac{x^3+2x+1}{x}\]

Solution:

Complete the square $5x^2+60x-13$. Give you answer in the form $A(x+B)^2+C$. Sketch the graph by starting with the parabola $y=x^2$.

Solution:

Let $f(x)=\dfrac{1+x}{2x+1}$ and $g(x)=\dfrac{3(1+x)}{1-4x}$.

1. Solve the equation $f(x)=g(x)$.
2. Simplify the expression $f\circ g(x)$.

Solution:

Simplify the expression \[\frac{(2^x x^2)^3}{\sqrt[3]{\frac{8^x}{x^6}}}\]

Solution:

Consider the functio \[f(x)=\begin{cases}\dfrac{x^2+x-6}{x-2}& x\neq 2\\ k& x=2\end{cases}\]

1. Using limits find k such that the function f(x) (a) is continuous at x = 2 and (b) is discontinuous at x = 2.
2. Sketch a graph clearly depicting the nature of f(x) at x = 2 in (a) and (b).

Solution:

Write the $f(x) = |2 − x|$ as a piecewise defined function. Using your answer, discuss the values of these limits if they exist:

1. $\displaystyle \lim_{x\to 2^-}\frac{|2 − x|}{x − 2}$
2. $\displaystyle \lim_{x\to 2}\frac{|2 − x|}{x − 2}$

Solution:

Compute: \begin{align} \lim_{h\to 0}\frac{\sqrt{x+h}-\sqrt{x}}{h}&=\\ \lim_{x\to 2^-}\frac{4-x^2}{x-2}&=\\ \lim_{x\to 1}\frac{4-x^2}{x-2}&=\\ \lim_{x\to 2^+}\frac{1-x^2}{x-2}&=\\ \lim_{x\to \frac{\pi}{2}^+}\frac{\tan x}{\sec x}&=\\ \lim_{x\to 0^+}\frac{e^{2x}-3e^x+1}{e^x-1}&=\\ \lim_{x\to 0}\frac{x}{\sqrt{4+x}-\sqrt{4-x}}&= \end{align}

Solution:

Find the derivative of each of the following functions with respect to the variable:

1. $\displaystyle f(x) = \sqrt{x}+\frac{\pi}{\sqrt{x}}$
2. $\displaystyle y =\frac{x^3+5x+6}{x}$
3. $\displaystyle h(t)=(2+\sqrt{t})t^2$

Solution:

1. $\displaystyle f'(x) = \frac{1}{2}x^{-1/2}-\frac{\pi}{2}x^{-3/2}$
2. $\displaystyle y' =2x-\frac{6}{x^2}$
3. $\displaystyle h'(t)=4t + \frac{5}{2}t^{3/2}$

Write the function \[f(x)=|x+2| - |7-x|\] as a piecewise defined function.

Solution:

Write the function \[f(x)=\frac{|x-5|}{5-x}\] as a piecewise defined function.

Solution:

Consider the function \[f(x)= \begin{cases} \frac{|x-5|}{5-x} & -\infty \lt x\lt 5\\ 24-x^2 & 5\leq x\lt 7\\ -3x-4 & 7\leq x\lt \infty \end{cases}.\]

1. Using limits and without graph, discuss the continuity of $f(x)$.
2. Write $g(x) = (f(x))^2$ a piecewise defined function. Discuss its continuity without graphing.

Solution:

Compute the limits: \begin{align} \lim_{x\to 0} \frac{(e^x-1)^2+e^{3x}+1}{e^{2x}+3} & =\\ \lim_{x\to 2^-} \frac{x^2-5x+6}{2-x} & = \\ \lim_{x\to 3}\frac{\sqrt{x+3}-\sqrt{x-3}}{3x} & = \end{align}

Solution:

Discuss the continuity of the function \[f(x)=\frac{|1-x^2|}{1-x}.\]

Solution:

For what values of $a$ and $b$ is the function \[f(x)=\begin{cases} \sqrt[3]{2x^4-5} & x\lt -2\\ a\sqrt{x+2}+b & -2\leq x\leq 2\\ \dfrac{2-x}{2+x-x^2}& 2\lt x \end{cases}\] continuous?

Solution:

The position (in feet) of a particle moving on a straight line is given by the function \[s(t) = \frac{5}{t}+t^e+2e^t+3^t.\] Find an expression for the (instantaneous) velocity $v(t)$. What is the velocity of the particle when $t = \ln 2$ seconds?

Solution:

Find the slope of the function $f(x) = (x^2 + 2)e^x$ at $x = 0$. What is the equation of the tangent line there?

Solution:

Water flows into a leaky container in such a way that the height of the water level from its base is given by $h(t) = \dfrac{4e^t + 3}{e^t + 3}$ inches.

1. Find the time t such the height of the water level is 3 inches.
2. Find the instantaneous rate of change (ROC) of the height of the water when the water level reaches 3 inches.

Solution:

The stationary points in the domain of a function $f(x)$ are the values of x such that $f'(x)=0$.

1. What can you say about the tangent line at stationary points?
2. Find the stationary points of \[y =\frac{2x-1}{x^2-1}.\]

   Solution:

If $\displaystyle f'(a)=\lim_{h\to 0}\frac{(3+h)^{10}-3^{10}}{h}$, what is a possible $f(x)$ and the value of $a$?

Solution:

The slope of the curve $y = ax^2 + bx$ at the point $(2, 4)$ is $−8$.

1. Calculate the values of a and b.
2. Calculate $\dfrac{dy}{dx}|_{x=-2}$ and use it to find the equation of the tangent line to the same curve at $x = −2$.

Solution:

Find the values of x for which the graphs of the functions $f(x) = x^3-3x^2+7x+8$ and $g(x) = \frac{1}{3}x^3-\frac{1}{2}x^2+5x-3$ have parallel tangent lines there. Pick one such location on the graph of f(x) and find the equation of the tangent line there.

Solution:

Let $p(x)=(x^3-5x+1)g(x)$ and $q(x)=\frac{f(x)}{g(x)+1}$. Given that $f(2) = 2$, $g(2) = 3$, $f'(2) = −1$ and $g'(2) = −4$, find the following values:

1. The instantaneous rate of change of p(x) at x = 2.
2. The slope of the tangent line to the graph of y = q(x) when x = 2.

Solution:

A military craft made with a new technology that could change its velocity on demand in a moment was test driven on a long straight road. The graph of its position s(t) for eight seconds of travel is given below. Sketch in the given axes below the velocity function v(t) indicating clearly places where velocity is undefined.

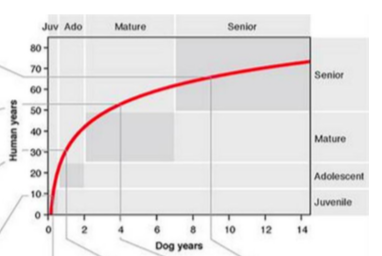
Solution:

Consider the function $f(t)=t^4-2e^t+2$.

1. Compute $f'(t)$, $f''(t)$, $f'''(t)$, and $\dfrac{d^4f}{dt^4}$.
2. If $f(t)$ represents the position of a particle moving on a straight line, what do $f'(t)$ and $f''(t)$ represent physically?

Solution:

Compute the limits \begin{align} \lim_{x\to 0}\frac{\sin 7x}{3x}&=\\ \lim_{x\to 0}\frac{\tan x}{2x}& \end{align}

Solution:

Solve the equations \begin{align} y&=\sqrt{3y-2}\\ 4^x&=3\cdot 8^x\\ 2&=\log_3(x+2)-\log_3(x-1)\\ \end{align}

Solution:

Classify the discontinuities of the function \[f(x)=\begin{cases} 2x+1 & x\lt -1\\ 0 & x=-1\\ -x-2 & -1\lt x \leq 0\\ x^2-1 & 0\lt x\lt 1\\ 3x+2 & 1\leq x\lt 2\\ 3 & x=2\\ \sqrt{5x-1} & 2\lt x \end{cases}.\]

Solution:

Compute the limits \begin{align} \lim_{x\to 3}\frac{\sqrt{x}-\sqrt{3}}{3-\sqrt{2x+3}}&=\\ \lim_{x\to 3}\frac{x+\sqrt{x+1}}{2^x-x^2}&=\\ \lim_{x\to 3}\frac{x^2-4x+3}{x^2-6x+9}&=\\ \lim_{x\to 1/3}\frac{3x^2-7x+2}{9x^2-1}&= \end{align}

Solution:

Consider the function $f(x)=2^x+\frac{x}{x+1}+\sqrt{x}\cdot\sqrt{x+1}$.

1. Compute the average rate of change of $f(x)$ over the interval $[0,3]$.
2. Find the instantaneous rate of change at $x=1$.

Solution:

Find a point where the tangent line to the graph of $f(t)=\dfrac{3t+1}{2t+3}$ is parallel to the line $y=7x+15$. Then find an equation for this tangent line.

Solution:

Consider the function \[f(x) =\begin{cases} x\sin \frac{1}{x}& x\neq 0\\ 1& x=0\end{cases}\]

1. Using limits describe the kind of discontinuity at $x = 0$.
2. How would you redefine $f(0)$ so that $f(x)$ is continuous for all $x$.

Solution:

Find an equation of the tangent line to the curve $y = \sec x − 2 \cos x$, at the point $(\pi/3, 1)$.

Solution:

Find the derivative of the following functions simplifying as far as possible. \[\frac{\sin x-\cos x}{\sin x+\cos x}\] \[x\tan x\sec x\]

Solution:

A piece if wood floating on the surface of a pond is bobbing up and down according to the position function \[s(t)=\cos (t)+\sin(t),\] given in cm, where $t$ is time in seconds.

1. Find formulas for both its velocity and acceleration at time t seconds.
2. Find the smallest value of $t$ at which the velocity of the piece of wood is zero.

Solution:

A heated cylindrical rod expanses in such a way that its height is always the square of its radius. If the height at time t minutes is given by $h = e^{−t} + 5$ in, find the rate of change (ROC) of the volume of the rod with respect to time when

1. $h = 8$ inches; and
2. $t = 1$ minute.

Solution:

Find the derivative of the following functions:

1. $\displaystyle f(x)=\sqrt[3]{1+x^3}$


2. $\displaystyle R=\csc^3(\pi x)$

Solution:

Find the equation of the tangent line at $x=0$ to the graph $y=\sqrt{x^2+1}\cdot e^{x^2+1}$.

Solution:

Find the derivative of the following functions:

1. $\displaystyle g(x)=\cot 5x$


2. $\displaystyle h(x)=\frac{1}{2}x^2\sqrt{16-x^2}$


3. $\displaystyle w=\left(\frac{t+1}{t^2+2}\right)^4$


4. $\displaystyle y=\tan^3(2x^2+1)$

Solution:

Let $f(x) = (x^3-5x+1)^2g(x)$. Given that $f(2) = 2$, $g(1) = 3$, $f'(2) = −1$ and $g'(1) = −4$ find the values of $g(2)$ and $f'(1)$.

Solution:

Find the coordinates of the points on the curve $y = 2xe^{−x^2}$ where the tangent lines are horizontal.

Solution:

Find the equation of the tangent line to the graph of $y =\dfrac{\ln x − 1}{\ln x + 1}$ when $x = 1$.

Solution:

Find the derivatives of the following functions:

1. $f(\theta)=\ln(\sin\theta+2)$.
2. $y=\ln\left(\dfrac{e^x-1}{e^x+1}\right)$.
3. $g(z)=\ln(\ln(z))$, $z>1$.
4. $y=e^{(\ln x)^3}+\ln(e^x)$.

Solution:

Find the derivative of the following functions:

1. $\displaystyle y=x^{\cos x}$.


2. $\displaystyle z=(1+1/x)^x$.

Solution:

Find the equation of the tangent line at the point P(1, 2) on the circle $x^2+y^2=5$ by solving for y as an appropriate expression of x.

Solution:

Consider the curve $x^3 + y^3 = 2xy$.

1. Verify that the point (1, 1) is on the curve.
2. Find $\frac{dy}{dx}$.
3. Find the slope of the curve at (1,1).

Solution:

Find $\frac{dy}{dx}$ if $\cos(xy)=x+y^2$.

Solution:

Determine whether the following functions are of the form $[f(x)]^n$, $a^{g(x)}$, and $[f(x)]^{g(x)}$ where a and n are constants, and f(x) and g(x) are functions of x. Find their derivatives.

1. $\displaystyle y=(2x^2+5)^{e^2+3}$.
2. $\displaystyle y=(2x^2+5)^{e^x+3}$.
3. $\displaystyle y=(2\pi^2+5)^{x^2+3}$.
4. $\displaystyle y=(\sin e +\cos^2 e)^{x^2}$.
5. $\displaystyle y=(\sin e+\cos^2 e)^{\pi^2}$.
6. $\displaystyle y=(\sin x+\cos^2 e)^{e^2}$.

Solution:

Find the points on the curve $x^4 = 4(4x^2 − y^2)$ for which the tangent lines to the curve are horizontal.

Solution:

A particle is moving along the curve $y =\sqrt{x}$. As the particle passes through the point (4, 2), its x-coordinate increases at a rate of 3 cm/s.

1. How fast is the y-coordinate changing at this instant?
2. How fast is the distance from the particle to the origin changing at this instant?

Solution:

A spotlight on the ground shines on a wall 12 m away. If a man 2 m tall walks from the spotlight toward the building at a speed of 1.6 m/s, how fast is his shadow on the building decreasing when he is 4 m from the building.

Solution:

The altitude of a triangle is increasing at a rate of 1 cm/min while the area of the triangle is increasing at a rate of 2 cm²/min. At what rate is the base of the triangle changing when the altitude is 10 cm and the area is 100 cm²?

Solution:

Determine the equation of the tangent line at $(0,\sqrt{e})$ to the curve $e^{xy} = \ln(x^2+y^2)$.

Solution:

Differentiate the functions \[f(x)=3^{\ln^2(\sin^3(\cos^4(\sqrt{x})))}\ \ \ \ \ \ \ g(x)=(\cos x)^{\sin x}.\]

Solution:

Water is leaking out of a conical tank with pointed end down at the rate of 9 ft³/min. The tank is 4 feet high and the radius at the top is 3 feet. At what rate is the water level changing when the water is 2.5 feet deep?

Solution:

A boat is pulled into a dock by a rope attached to the bow of the boat and passing through a pulley on the dock that is 1 m higher than the bow of the boat. If the rope is pulled in at a rate of 1 m/s, how fast is the boat approaching the dock when it is 8 m from the dock?

Solution:

A 5 meter long ladder leaning against a vertical wall such that one end is on the wall and the other end is on the ground about 0.5 meter away. If the top end of the ladder is slipping down the wall at a constant rate of 1/4 meter/min, how fast is the lower end of the ladder on the ground moving away from the wall when the lower end is 3 meters from the bottom of the wall?

Solution:

By eliminating the parameter, find the cartesian equation for the curve given by parametric equations: \[x=\ln(t+2)\ \ \ \ y=t^2+3.\]

Solution:

The population of wolves w(t) and wild boars p(t) in the thousands are given by the equations: \[w(t) = 3 \sin t + 5\ \ \ \ \ \ p(t) = 2 \cos t + 5.\]

1. Find a relation between w and p.
2. Draw its graphs and describe what is happening between the two populations.

Solution:

Compute the derivatives of the following functions:

1. $\displaystyle y = (\pi+e^3)^{1/x}$.


2. $\displaystyle y = (\ln x+\tan x)^{\ln \pi}$.


3. $\displaystyle y = (\cos x)^{\sin x}$.

Solution:

The linearization/linear approximation/tangent line approximation of $f(x)$ close to $x=c$ is the equation of the tangent line at $x=c$.

Find the linearization (tangent line approximation) of $\sqrt{x}$ at $x = 25$. Estimate $\sqrt{25.5}$. Draw a graph to illustrate your estimation. Is your estimate an overestimate or underestimate?

Solution:

Consider $f(x) = \ln(x^2) + x^3$.

1. Use linear approximation to estimate the value of $\Delta f$ as x changes from $x = 1$ to $x = 1.05$.
2. Estimate the percentage change of f when x changes from $x = 1$ to $x = 1.05$.

Solution:

If $g(3) = 4$ and $g'(3) = −1$, estimate $\Delta g$ and the percentage change of g as x changes from 3 to 3.01. Estimate g(3.01).

Solution:

The diameter of a circular disk is given as 10 cm with a maximum error in measurement of 0.2 cm. Use estimate the maximum error ($\Delta A$) and percentage error in the calculated area of the disk. If the disk is made with an expensive titanium sheet that costs $\$50$ per cm², estimate an upper limit for your budget in making a disk of 10 cm diameter.

Solution:

A vessel is in the shape of an inverted cone. The radius of the top is 5 cm and the height is 8 cm. Water is poured in to a height of x cm. Find an expression for the volume V of the water in the vessel in terms of x. Hence use calculus to find the approximate increased in V when x increases from 4 cm to 4.08 cm. Give units for your answer.

Solution:

Consider the point $(0,1)$ on the curve $\ln(x+y^2) = \cos(x)+\sin(\pi y^3/2)$. Estimate the percentage change in $y$ if $x$ changes from $0$ to $0.02$.

Solution:

A bungee cord is tied to two stakes, A and B, placed 20 ft apart. A hook is tied to the cord 12 ft from A. The hook is then lifted with 2 ft/min, elongating the bungee cord. What is the rate of change of the total length of the cord when the hook is 3 ft in the air?

Solution:

Find the linear approximation of $y=\cos^3(e^{4\theta})$ around $\theta=0$ and estimate $y$ when $\theta=0.01$.

Solution:

In 2002 I (Andrei) took a physics class where the final grade was computed as \[y = \frac{2H}{3}+\left(1-\frac{2H}{3}\right) F^{4/(5E^2)},\] where $H$ is the homework grade, $F$ is the final exam grade, and $E$ is a mysterious effort grade, all out of 1 (i.e., 100%). Suppose $E=1$, $H=0.9$ and $F=0.9$. Suppose $H$ is increased to $9.01$. Estimate by what percentage should $F$ change to keep the final score the same?

Solution:

(Textbook 3.4.26) The power delivered by a battery to an apparatus of resitance $R$ is $P = 2.25R/(R+0.5)^2$ ohms. When $R=3$ ohms a fluctuation occurs that changes resistance by $2\%$. Estimate the percentage change in power.

Solution:

We know that $f = \sqrt[3]{g^2}$ and $g=\log_2(h^2+3)$. If $h(1)=1$ and $h'(1)=2$ what is the rate of change of $f$ when $t=1$?

Solution:

Find all critical points of $\displaystyle f(x) = x − \frac{3}{2}x^{2/3}$ for $−1 \leq x \leq 1$ and determine the maximum and minimum values of $f(x)$ for $−1 \leq x \leq 1$.

Solution:

Find the absolute (global) maximum and minimum of the function $\displaystyle f(x) = \frac{1}{4}x^4-\frac{1}{3}x^3-x^2+1$ on the interval [0, 3].

Solution:

The sides of a rectangular box with a square base is growing at 0.5cm/sec.

1. How fast is its volume increasing when the dimensions of the box is 5cm x 5cm x 12cm?


2. How fast is the diagonal of the box (the longest distance between two opposite corners) changing at the same instant?


3. Consider the angle between the diagonal of a rectangular face and the edge of the square base. How fast is this angle changing at the same instant?

Solution:

A 10 meter long tank in the shape of a prism is slowed filled with water such that the depth of the water is increasing at 0.1 m/hour. If the dimensions of the triangular cross-section is as shown below,

1. find how fast is the volume of the tank changing when the depth of the water is 2 meter.


2. Find also how fast is the width of the water surface changing at the same moment and (c) how fast is the area of the water surface changing at the same moment.

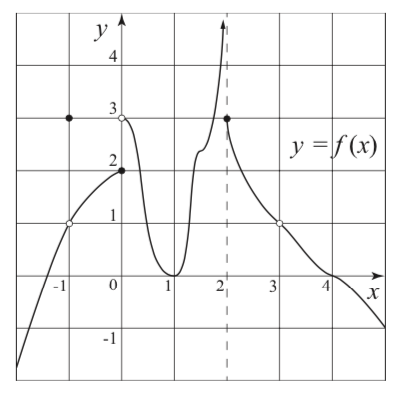
Solution:

Consider the curve $C$ given parametrically by $x=e^t+e^{-t}$ and $y=e^t-e^{-t}$.

1. Find the coordinates of all the points on C such that the slope to the curves at these points is 2. Find the equation of the tangent line to each point you found.


2. Find a Cartesian equation for the curve C.

Solution:

Finding Absolute Min and Max

1. Find critical points in (a,b)
2. Evaluate function at critical points and endpoints
3. Evaluate and pick out min and max

A piece of wire 10 m long is cut into two pieces. One piece is bent into a square and the other is bent into a circle. How should the wire be cut so that the total area enclosed is (a) maximum and (b) minimum?

Solution:

The lengths of the sides of a triangle are $9+x^2$, $9+x^2$ and $18-2x^2$. Calculate the area of the triangle and for which value of x this maximum is achieved.

Solution:

Verify that the function $f(x) = \dfrac{x}{x + 2}$ satisfies the hypotheses of the Mean Value Theorem on [1, 4]. Then find all numbers c that satisfies the conclusion of the Mean Value Theorem.

Solution:

A police observed Kelly Brian’s car passing his check point 8:00am at 62 mph. His patrolling buddy further down the 65mph-limit highway observed Kelly Brian’s car 8:45am at 65 mph. Assuming that the highway is fairly straight and the two police are about 56 miles apart, can you conclude that Kelly Brian has been obeying the speed limit in the duration between 8am to 8:45am?

Solution:

What is the smallest total area of a cylinder of volume $\pi$ ft³? The cylinder's height must be between 0.01 ft and 100 ft.

Solution:

Find the critical points of the following functions:

1. $f(x)=x-4\sqrt{x+1}$.


2. $g(t) = t+|2t+1|$.

Solution:

Find the absolute maximum and minimum values of the function $y=\sqrt{x^2-1}-2x$ in the interval $[1,2]$.

Solution:

Find $\dfrac{dy}{dx}$ if $\tan(xy) + y^2 = y + 1$. Find the linear approximation around the point $(\pi/4,1)$.

Solution:

Find a point $c$ satisfying the MVT (Mean Value Theorem) for the function $y=e^x-x$ over the interval $[-1,1]$.

Solution:

Find all values of x for which $f(x) = x^3 + 3x^2 − 9x + 3$ is increasing or decreasing with the steps outlined below. Classify all critical points using first derivative test.

1. Find all critical points of f.
2. Find points where f have a vertical asymptote or undefined.
3. Draw a number line, mark all points found in Steps 1 and 2, and find the sign of $f'(x)$ in each intervals between marked points.
4. Write down the values of x for which f is increasing/decreasing.
5. Classify all critical points using first derivative test.

Solution:

Determine the monotonicity of $\dfrac{\ln x}{x}$, i.e., the intervals where it is increasing/decreasing and the local maxima/minima.

Solution:

Suppose $f(x)$ is such that $\displaystyle f'(x)=\frac{x^2+3}{x-1}$. Find all points of inflection and concavity of f(x). (While not necessary, here is an example of such a function $f(x)=\frac{1}{2}(x+1)^2+4\ln|x-1|$.)

Solution:

Find all relative extrema for the function $f(x) = x^3 −9x^2 + 27x$. Use second derivative test to classify them.

Solution:

Use L'Hopital, if possible, for the following limits.

1. $\displaystyle \lim_{x\to 0}\frac{\sin x+\sin(2x)}{x-\sin(4x)}$.


2. $\displaystyle \lim_{x\to\infty}\frac{\sin x+\sin(2x)}{x^2+1}$.


3. $\displaystyle \lim_{x\to\infty}\frac{\ln(1+x)}{x}$.


4. $\displaystyle \lim_{x\to \infty}\frac{3e^{3x}+4e^x+5}{2e^{3x}+e^x+3}$.

Solution:

Use L'Hopital, if possible, for the following limits:

1. $\displaystyle \lim_{x\to 0^+}x\ln(x)$.

Solution:

Use L'Hopital, if possible, for the following limits:

1. $\displaystyle \lim_{x\to \infty}(1+x)^{1/x}$.


2. $\displaystyle \lim_{x\to \infty}\left(1-\frac{2}{x}\right)^x$.


3. $\displaystyle \lim_{x\to 0^+}x^x$.

Solution:

Determine the intervals over which the following functions are increasing and decreasing, and find all points of local extrema.

1. $f(x)=x^{2/3}-x$.


2. $g(x)=x^{-x}$ for $x>0$.

Solution:

For the following functions find the intervals where the functions are concave up/down, the inflection points, and points of relative extremum, which you should classify using the 2nd derivative test.

1. $f(\theta)=\theta+\sin(\theta)$ for $\theta$ in the interval $[0,2\pi]$.


2. $y=\ln(x^2+2x+5)$.

Solution:

Use L'Hopital, if possible, for the following limits:

1. $\displaystyle \lim_{x\to 0}\frac{\sqrt{1+x}-\sqrt[3]{1+x^2}}{3x}$.


2. $\displaystyle \lim_{x\to 0^+}\sin(t)\ln(t)$.


3. $\displaystyle \lim_{x\to 0^+}x^x$.

Solution:

Use L'Hopital, if possible, for the following limit:

1. $\displaystyle \lim_{x\to 0^+}\csc x-\cot x$.

Solution:

Find the all vertical and horizontal asymptotes of the following functions:

1. $\dfrac{x-2}{x^2-4}$


2. $\dfrac{x^2-2}{x^2-4}$


3. $\dfrac{x^3-2}{x^2-4}$

Solution:

Sketch the graph of $g(x) = xe^{−x^2}$ by completing the steps below.

1. Find all x-intercepts and y-intercept of the graph of g(x) whenever possible.


2. Find coordinates of all critical points, vertical asymptotes, and places where g(x) are undefined.


3. Determine where g(x) is increasing and where it is decreasing.


4. Determine the concavity and coordinates of inflection points of g(x).


5. Find all asymptotes and limit at infinity whenever applicable. Check for any symmetry.


6. Sketch the graph below labeling all important features. Your picture should be large and clear.

Solution:

Find all vertical and horizontal asymptotes of \[y =\frac{3e^{3x} + 4e^x + 5}{2e^{3x} + e^x + 3}.\]

Solution:

Sketch the graph of $g(x) = \dfrac{e^x+1}{e^x-1}$ by completing the steps below.

1. Find all x-intercepts and y-intercept of the graph of g(x) whenever possible.


2. Find coordinates of all critical points, vertical asymptotes, and places where g(x) are undefined.


3. Determine where g(x) is increasing and where it is decreasing.


4. Determine the concavity and coordinates of inflection points of g(x).


5. Find all asymptotes and limit at infinity whenever applicable. Check for any symmetry.


6. Sketch the graph below labeling all important features. Your picture should be large and clear.

Solution:

Find the absolute (global) maximum and minimum of $f(x) = xe^{−x}$ on the interval [0.5, 2]. Write down the range of the values of f(x) for $0.5 \leq x \leq 2$.

Solution:

Using the steps below, find the global maximum and minimum of $f(x) = xe^{−x}$ on $[0.5, \infty)$.

1. Find all critical points in the domain of f(x) and the values of f(x) there. Classify them using first derivative test.


2. Find the values of f(x) at the end-points (if any) of its domain.


3. If end-point not included, or $\pm\infty$, find all limits of f(x) towards end of interval.


4. Give a schematic sketch (ignore concavity) of the graph of f(x) clearly indicating where the global maximum and minimum are. State the global maximum and minimum of f(x) on $[0.5, \infty)$ if any. Find the range of f(x) for x in $0.5 \leq x \lt \infty$.

Solution:

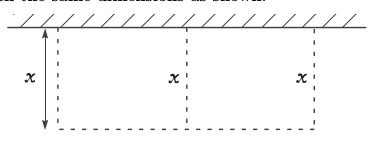
A landscaper plans to use 120 m of fencing and a very wide straight wall to make two rectangular enclosures with the same dimensions as shown.

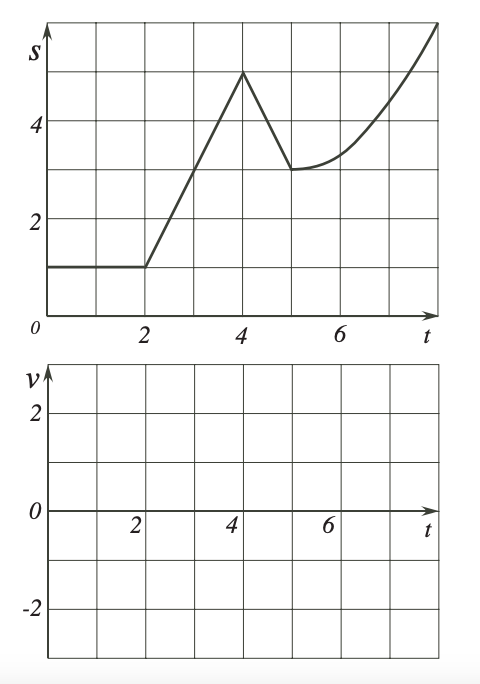
1. Write down the possible values of x.


2. Find the maximum value of the total area of the enclosures. What are the dimensions of each enclosure when maximum occurs?

Solution:

The top and bottom margins of a poster are each 6 cm and the side margins are each 4 cm. If the area of printed area on the poster is fixed at 384 cm², find the dimensions of the poster with the smallest area.

Solution:

A rancher will use 600m of fencing to build a corral in the shape of a semicircle on top of a rectangle. Find the dimensions that maximize the area of the corral.

Solution:

Find two positive numbers $x$ and $y$ such that they add up to 120 and $x^2y$ is as large as possible.

Solution:

Plot one of the following functions following the steps below: $f(x)=\sin(x)-\frac{1}{2}\sin(2x)$ over $[0,\pi]$, $g(x)=\dfrac{1}{x^2-6x+8}$, and $h(x)=x^{-x}$ for $x>0$.

1. Find all x-intercepts and y-intercept of the graph of g(x) whenever possible.


2. Find coordinates of all critical points, vertical asymptotes, and places where g(x) are undefined.


3. Determine where g(x) is increasing and where it is decreasing.


4. Determine the concavity and coordinates of inflection points of g(x).


5. Find all asymptotes and limit at infinity whenever applicable. Check for any symmetry.


6. Sketch the graph below labeling all important features. Your picture should be large and clear.

Solution:

Find the point on the hyperbola $y =\dfrac{1}{2\sqrt{x}}$ that is closest to the point (0, 0).

Solution:

A cylindrical can without a top is made to contain 100 cm³ of liquid. Find the dimension that will minimize the cost of the material to make the can if the material for the side costs $2/cm² and the material for the base costs $3/cm².

Solution:

Find the area of the largest rectangle that can be inscribed in a right triangle with legs of lengths 3cm and 4cm if two sides of the rectangle lie along the legs.

Solution:

A piece of wire 10 m long is cut into two pieces. One piece is bent into a square and the other is bent into a circle. How should the wire be cut so that the total area enclosed is (a) maximum and (b) minimum.

Solution:

Show that of all the isosceles triangles with a perimeter of 30 cm, the one with the largest area is equilateral.

Solution:

Find the point on the parabola $y^2 + x = 0$ that is closest to the point (0, −3).

Solution:

Find the dimensions of a closed cylindrical can with maximum volume if the surface area is $200\pi$ cm².

Solution:

A 100 meter long wire is to be bent into a shape consisting of a semi-circular side and two equal straight sides. Find the dimensions of the shape if the area enclosed is to be maximized. Your answer should give the radius of the semi-circular side and the length of the two equal straight sides.

Solution:

Consider a shape consisting of a semi-circular side and two equal straight sides which encloses an area of 100 sq. meters. Find the dimensions of the shape if its perimeter is to be shortest. Your answer should give the radius of the semi-circular side and the length of the two equal straight sides.

Solution:

Consider the function $f(x)=x^3+x+1$.

1. Find $f'(x)$.


2. Explain why we could see that f(x) has a unique zero in the interval [−1, 0].


3. Apply Newton’s Method with $x_0 = -0.5$ to estimate the zero of f(x) up to three decimal places.

Solution:

Estimate all solutions of $x^2 = \cos x$ up to four decimal places.

Solution:

Find the range of the function $f(x)=x^{-x}$ for $0\lt x\lt \infty$.

Solution:

Compute the limit \[\lim_{x\to 0}\left(\frac{e^x}{e^x-1}-\frac{1}{x}\right).\]

Solution:

Find the maximum length of a pole that can be carried horizontally around a corner joining corridors of widths $a=24$ and $b=3$.

Solution:

What happens if you apply Newton's method to solving the equation $x^3-2x+2=0$ starting with the initial guess $0$? [Hint: You won't find a solution!]

Solution:

Explain how to determine the solutions of $\ln(x+4)=x$ up to 5 decimal places by writing the formula you would input into a spreadsheet.

Solution:

Explain why L'Hopital gives no information about the limit \[\lim_{x\to \infty}\frac{2x-\sin x}{3x+\cos(2x)}\] and evaluate the limit by some other means.

Solution:

\begin{align} \int k dx &=\\ \int x^k dx &= \\ \int \frac{1}{x}dx &=\\ \int k f(x) dx &= k\int f(x)dx\\ \int (f(x)+g(x))dx &= \int f(x)dx + \int g(x)dx\\ \int e^x dx &=\\ \int e^{ax}dx &=\\ \int a^x dx &= \end{align}

Solution:

Evaluate the following indefinite integrals:

1. $\displaystyle \int (1+e^{2x}+e^2+3x-x^2)dx$.


2. $\displaystyle \int\frac{2u^2-5u+\sqrt[3]{u}}{u^2}du $.

Solution:

Find the antiderivative F of function f satisfying the given condition: \[f(x)=(e^x+1)^2\ \ \ \ \ F(0)=3.\] In other words, solve the initial value problem $F(0)=3$, $\frac{dF}{dx}=(e^x+1)^2$.

Solution:

A ball is projected upward from the ground with an initial velocity of 3 m/sec. Using calculus, write the velocity and position for the ball at time t. You may assume that the acceleration due to gravity is 10 m/s².

Solution:

A small piece of wood is bobbing up and down on the surface of a pond with its acceleration given by \[a(t) = (\sin t − \cos t) m/s^2.\] Given that the cork has velocity 1 m/s and position −2 m when $t = \pi$ seconds, answer the following questions:

1. If s(t) is the position of the cork, write in terms of s and its derivatives, a differential equation, and initial value conditions modeling the position of the cork.
2. Solve the equation in (1) for s(t) by first finding for $s'(t)$.

Solution:

Evaluate the following indefinite integrals:

1. $\displaystyle \int\frac{\tan \theta}{\cos\theta}d\theta=$


2. $\displaystyle \int\frac{1+\cos^2\theta}{\cos^2\theta}d\theta=$

Solution:

Assuming that the pattern in the sums below, write down (a) the formula for the general term, and (b) the sum using summation notation.

1. $\dfrac{5}{1+1^2}+\dfrac{5}{1+2^2}+\dfrac{5}{1+3^2}+\cdots+\dfrac{5}{1+15^2}$.


2. $\dfrac{5}{1+5^2}+\dfrac{5}{1+6^2}+\dfrac{5}{1+7^2}+\cdots+\dfrac{5}{1+13^2}$.


3. $\left(\dfrac{1}{n}\right)\sqrt{1-\left(\dfrac{0}{n}\right)^2}+\left(\dfrac{1}{n}\right)\sqrt{1-\left(\dfrac{1}{n}\right)^2}+\left(\dfrac{1}{n}\right)\sqrt{1-\left(\dfrac{2}{n}\right)^2}+\cdots+\left(\dfrac{1}{n}\right)\sqrt{1-\left(\dfrac{n-1}{n}\right)^2}$.

Solution:

If $a_0 = 2$, $a_1 = 0$, $a_2 = −1$, $a_3 = −2$, and $a_4 = 0$. Find the value of the sums:

1. $\displaystyle \sum_{j=2}^4(2a_j+3) = $


2. $\displaystyle \sum_{n=0}^2\cos(a_n\pi) = $

Solution:

Consider the function $f(x)$ with the following graph:

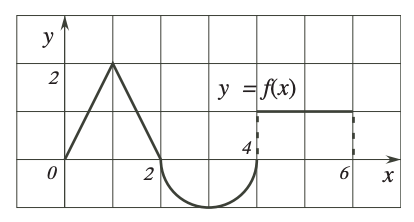
1. Find the Riemann sum for f(x) over [0, 2] using 4 equal subintervals and the left endpoints.


2. What value would you obtain if you allowed more and more subintervals?

Solution:

Consider the function $g(x)$ with the following graph:

1. Find the Riemann sum for g(x) over [0, 2] using 4 equal subintervals and the right endpoints.


2. What value would you obtain if you allowed more and more subintervalss?

Solution:

At time $t=1$ with initial velocity $4$ m/s a particle moves in a straight line with acceleration $a(t)=3\sqrt{t}$ m/s². Find the distance traveled after 25 s.

Solution:

Solve the differential equation $\dfrac{dy}{dx}=e^{-x}+\dfrac{1}{\sqrt{x}}$, $y(0)=0$.

Solution:

Find $M_4$ for $f(x)=2^{-x}$ in the interval [1,3].

Solution:

* What area is \[\lim_{N\to\infty}\frac{5}{N}\sum_{j=0}^{N-1}e^{-2+5j/N}\] approximating?

Solution:

Consider the graph of f(x) below:

1. $\displaystyle \int_0^2 f(x)dx=$


2. $\displaystyle \int_1^4 f(x)dx=$


3. $\displaystyle \int_2^4 f(x)dx=$


4. $\displaystyle \int_0^6 f(x)dx=$

Solution:

Given that $\displaystyle \int_0^2 f(x)dx=\int_2^3 f(x)dx=5$ find

1. $\displaystyle \int_0^3 f(x)dx=$


2. $\displaystyle \int_0^2 (4f(x)+2)dx=$


3. $\displaystyle \int_0^2 f(x)dx+\int_3^2 f(x)dx=$


4. $\displaystyle \int_{-3}^0 f(x)dx=\ \ \ \ \ \ $ if $f(-x)=f(x)$.

Solution:

Evaluate the following definite integrals:

1. $\displaystyle \int_{-1}^0(1+3x-e^{-x}) dx=$


2. $\displaystyle \int_{\pi/2}^\pi\cos\theta d\theta=$


3. $\displaystyle \int \sqrt{x-1}dx=$


4. $\displaystyle \int_1^5 \sqrt{x-1}dx=$

Solution:

Evaluate the following integrals using the method of substitution:

1. $\displaystyle \int x\sqrt{2-3x}dx =$


2. $\displaystyle \int_1^4\frac{1}{x^2}\sqrt{1+\frac{1}{x}}dx =$

Solution:

1. The change in the displacement of the particle over the duration [3, 6].


2. The displacement of the particle after 2 minutes.


3. The furthest distance covered by the particle to the left of its origin.

Solution:

Find the derivative of each of the following functions:

1. $\displaystyle g(x)=\int_2^x t^2\sin t dt$


2. $\displaystyle F(x)=\int_x^2 \cos(t^2)dt$


3. $\displaystyle y=\int_3^{\sqrt{x}}\frac{\cos t}{t}dt$


4. $\displaystyle z=\int_1^{\cos x}(u+\sin u)du$

Solution:

Evaluate the following integrals:

1. $\displaystyle \int_0^{\pi/4}\sin 4\theta d\theta$


2. $\displaystyle \int_1^2 x^2e^{x^3+2}dx$


3. $\displaystyle \int\frac{t+1}{t^2+2t+5}dt$

Solution:

Water flows into a large tank at rate r(t) liters/min given in the table below. If the initial volume of water is 100 liters, estimate the volume of water in the tank at t = 4 minutes using left-endpoint approximation. \begin{array}{l|l|l|l|l|l|l|l} t&0&1&2&3&4&5&6\\ \hline r(t)&10&15&18&20&23&21&25 \end{array}

Solution:

Find the total distance traveled by a particle with velocity $v(t) = 4t − t^2$ over the time duration $1 \leq t \leq 6$. What is the change in displacement over the same duration?

Solution:

Evaluate the following integrals:

1. $\displaystyle \int t^3\sec^2(t^4+1)dt$


2. $\displaystyle \int e^{e^x+x}dx$


3. $\displaystyle \int_0^{\pi/2}\sin(2\theta+\pi)\cos^3(2\theta+\pi)d\theta$

Using right-endpoint approximation, estimate the area A under the curve y = f(x) over [2, 8] from the following data for f. Assume that f(x) is positive value. \begin{array}{l|l|l|l|l|l|l|l} x&2&3&4&5&6&7&8\\ \hline f(x)&30& 35& 38& 42& 44& 46& 48 \end{array} Assuming that f is strictly increasing, is the estimate you found a lower or upper estimates for A?

Solution:

Compute the derivative of the following function \[f(x)=\int_{\sqrt{x}}^{\ln x} \frac{t+\sin t}{\ln(1+t)}dt.\]

Solution:

Continuity and limits including piecewise defined function, left and right continuity, jump discontinuity, and removable continuity.
Tools: left and right limits, value at point.

Derivative of a function including average rate of change (or difference quotient) and limit definition of the derivative (or instantaneous rate of change) of a function.
Tools:

Application of derivatives including slope of the graph of a function, equation of tangent line and linearization, higher derivatives, position, velocity and acceleration of a particle moving on a straight line.
Tools: Derivative is a slope and a rate of change.

All rules for computing derivatives including power rule, product rule, quotient rule, chain rule.

Application for Chain rule including implicit differentiation, related rate, logarithmic differentiation and parametric equation.

Graphing Concepts: Monotonicity and critical points of a function, Concavity and inflection points of a function and Asymptotes of the graph of a function and limits of a function.
Tools: Sign of $f'(x)$ and $f''(x)$. The number line. L'Hopital.

Optimization of a function
Tools: Critical points and values/limits at the endpoints.

Antiderivatives and initial value problems.
Tools: Find the constant C by plugging in the initial value.

Riemann sums and definite integrals including method of substitution.

Find all asymptotes and describe the points of discontinuity of the function $\dfrac{2^{2x}-2^{2+x}+3}{2^{2x}-3\cdot 2^x+2}$.

Solution:

Find the maximum area of a rectangle circumscribed around a rectangle of sides 2 and 3.

Solution:

A particle is traveling along the curve $x^3+xy+y^3=11$. How fast is the distance to the origin changing if the $y$-coordinate of the particle is descreasing at a rate of 1m/s and the particle is at the location (2,1)?

Solution: