Math 10360 Calculus B In-class Exercises
Week 1
+
+
+
Find the area under the graph of $y =\dfrac{−2}{4x − 3}$ for $0 \leq x \leq 1/2$.
Find the equation of the tangent line to the curve $y = 4−2e^x + \ln \left(\dfrac{1 − x^2}{1 + x^2}\right)$ at $x = 0$.
+
Using the log function find the derivative of $\displaystyle y=(1+2x)^{\arctan x}$.
Find the derivative of $z=\arcsin(2x+y^2)$:
- with respect to $x$, treating $y$ as a constant, and
- with respect to $y$, treating $x$ as a constant.
A population $y(t)$ (in millions of units) of bacteria grows according to the rate $\displaystyle \frac{dy}{dt}=\frac{1}{1+4t^2}$. Find the total change in the size of the population over the time duration $0\leq t\leq 1/2$.
Week 2
+
The slope at each point of the graph of $f(x)$ is given by \[\frac{2x+1}{4+x^2}.\] Find a formula for $f(x)$ if its graph passes through the point $(2,0)$.
+
Compute the following integrals:
- $\displaystyle \int_0^1\frac{x+2x^3}{1+x^2+x^4}dx=$
- $\displaystyle \int\frac{1}{\sqrt{4-9x^2}}dx=$
- $\displaystyle \int\frac{4+x}{\sqrt{1-9x^2}}dx=$
- $\displaystyle \int_0^{\ln 2}\frac{e^t}{1+e^{2t}}dt=$
- $\displaystyle \int \frac{e^{2t}}{1+e^{2t}}dt=$
+
The population $P(t)$, at time $t$ hours of a bacteria is given by $P(t) = 5e^{2t}$ in thousands.
- What is the initial population of the bacteria?
- Give a formula for the growth rate of the population of the bacteria.
- What did you observe about the growth rate?
- Explain what is meant by the doubling time for the population. Find this time.
Recent experiments on viability of the coronavirus indicates that it reduces exponentially on various surfaces. The half life of the coronavirus on glass is estimated to be about 14 hours.
- Starting with 100% initially, find a formula in the form $A \cdot e^{rt}$ for the percentage of the virus on glass after t hours.
- If we consider the virus no longer infectious (or viable) after it is reduced to 1% or less, estimate how long will the virus remain infectious on glass.
A cypress beam found in the tomb of Sneferu in Egypt contained 55% of the amount of Carbon-14 found in living cypress wood. Estimate the age of the tomb given that Carbon-14 has a half-life of 5730 years.
+
Find the area enclosed by the graphs of $y = x^3 − x$ and $y = 3x$. Give a sketch of the graphs first.
Find the area bounded between the two curves $x=\sin y$ and $x=\sin 2y$ for $0\leq y\leq\pi$. (You may use the identity $\sin 2y = 2 \sin y \cos y$.)
Find the volume of the solid shown below by integrating the area of vertical cross-section perpendicular to the x-axis.
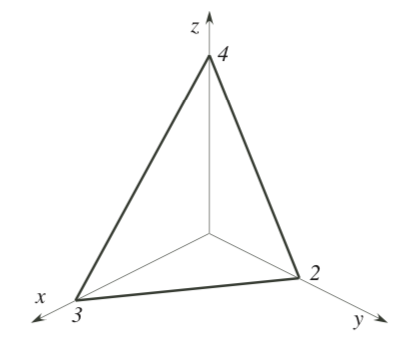
Week 3
+
Consider a solid whose base is the region bounded by the lines $y = x^3$, $y = 8$, and the y-axis. Find the volume of the solid in each of the following cases:
- The cross sections perpendicular to the y-axis are squares.
- The cross sections perpendicular to the y-axis are rectangles of height $\sqrt{y}$.
- The cross sections perpendicular to the y-axis are semicircles.
Find the total mass of the a 5 meter rod whose linear density is given by $\displaystyle \rho(x) = \frac{e^x}{(1+e^x)^2}$ g/m for $0 \leq x \leq 5$.
+
A variety of deep sea worm is distributed about a hydrothermal vent according to the population density $\displaystyle \rho(r) = \frac{8000}{9 + r^2}$ thousand per sq. miles where $1 \leq r \leq 3$ is the distance (in miles) from the vent. Find the total population of the sea worm.
Find the average amount of money over the first 10 years in an account earning interest at an annual rate of 4% compounded continuously if the principal is $5000. Draw a graph of the balance in the account and mark the value that represents the average amount of money. Find the time it takes the account to reach this average.
Compute the volume of a paraboloid which lies above the region in the plane bounded by the parabola $x=3-y^2$ and the $y$-axis, and whose cross-sections perpendicular to the $x$-axis are all discs. Set up the integral only.
Find the volume of liquid needed to fill a sphere of radius $R$ to height $h$. Set up the integral only.
Compute the average of the function $f(x)=\sec^2 x$ over the interval $[\pi/6, \pi/3]$.
Find the mass of a disc of radius $2$ cm whose radial density is $\rho(r)=\frac{4}{r}$ g/cm2. (The answer is particularly surprising because at the center of the disc the density is infinite.)
What is the mass of a rod of 2m with density $\rho(x)=\frac{x^2}{1+x^2}$?
+
A semicircular plate of radius 3 in. has radial weight density $\rho(r) =\frac{3}{\sqrt{r}}$ lb/in . Find the total weight of the plate.
Find the volume of the solid formed by rotating the region between the curve $y = 4 − x^2$ and the x-axis for $−2 \leq x \leq 2$ about
- the x-axis,
- the line $y = −1$, and
- the line $x = 3$.
+
Find the volume of the solid obtained by rotating the region bounded by the given curves about the specified line.
- $y=\frac{1}{x+2}$, $x=-1$, $x=0$, $y=0$, about the line $y=2$.
- $y=-x^2+2x$, $y=x$, about the $y$-axis.
A 300 kg chain 100 m in length is attached at one end to a crank on the top of a 300 m building, and the rest of the chain is allowed to hang freely on the side of the building from the crank.
- How much work is done when the whole chain is cranked up to the top of the tower?
- If a 20 kg weight is attached to the bottom end of the chain, how would the amount of work change? Assume that the chain has uniform linear density.
Week 4
+
Find the volume of the solid obtained by rotating the region bounded by $y=\frac{1}{x+2}$, $x=-1$, $x=0$, $y=0$, about the line $y=2$.
Find the volume of the solid obtained by rotating the region under the graph of $f(x)=\frac{1}{\sqrt{x^2+1}}$ over the interval [0,2] about the line $x=0$.
A 300 kg chain 100 m in length is attached at one end to a crank on the top of a 300 m building, and the rest of the chain is allowed to hang freely on the side of the building from the crank.
- How much work is done when the whole chain is cranked up to the top of the tower?
- If a 20 kg weight is attached to the bottom end of the chain, how would the amount of work change? Assume that the chain has uniform linear density.
+
A cistern is shaped like a cylinder of height 6 m and radius 10 m. The circular opening (10 m in radius) of the cistern is at ground level and the rest of the cistern is buried below ground. Compute the amount of work done (in Nm =Joules) in pumping all the water out of the cistern from ground level if it is filled completely with water. Mass density of water is 1000 kg/m3. You may take the acceleration due to gravity as $g = 10$ m/s2.
A 300 kg chain 100 m in length is attached at one end to a crank on the top of a 300 m building. The rest of the chain is allowed to hang freely on the side of the building from the crank. A 20kg weight is also added to the free end of the chain. How much work is done to crank three quarter of the chain with the weight attached to the top of the tower? Assume that the chain has uniform linear density. You may take the acceleration due to gravity as $g = 10$ m/s2.
Use discs, i.e., cross-sections perpendicular to the axis of rotation, to set up an integral that computes the volume of rotation about $y=12$ of the region in the 1st quadrant bounded by $y=9/x^2$ and $y=10-x^2$.
Use cyindrical shells to set up an integral that computes the volume of rotation around the x-axis of the region bounded by $y=x^{1/3}-2$, $y=0$, $x=27$.
Set up an integral, by any method you wish, that computes the volume of rotation around the line $x=4$ of the region bounded by $y=-x^2+4x-3$ and $y=0$.
+
A tank is shaped like an inverted right circular cone of height 12 m with circular opening of radius 3 m. Assuming that the tank is filled halfway up with a certain kind of oil, compute the amount of work done in pumping all the oil to a level 2 m above the opening of the tank. Density of the oil is 500 kg/m3. You may take the acceleration due to gravity as $g = 10$ m/s2.
A 10 m long uniform chain weighing 30 kg lying completely at the foot of a 50 m building.
- What is the work done to wrench one end to the top of the building with the rest of the chain dangling free from that end?
- What is the work done if the wrenched end of the chain is 30 m above ground?
- What is the work done if the wrenched end of the chain is 5 m above ground (with half of the chain left on the ground)?
A 10m chain with non-uniform linear mass density $\rho(y) = e^y$ kg/m for $0 \leq y \leq 10$ is coiled on the ground is lifted straight up from its heavier end (labelled A) so that End A is 10m above the ground and the rest of the chain dangles free below.
- Find the work done in lifting the chain. You may take the acceleration due to gravity as $g = 10$ m/s2.
- The same chain is now hanging at end A on the top of a 10m building with the rest of the chain dangling along the side of the building. Find the work done in lifting the whole chain to the top of the building.
- (Challenging) The same chain is again coiled on the ground. Find the work done in lifting 5m of the chain straight up at end A leaving the rest of the change on the ground.
+
Set up a definite integral that gives the volume of the solid formed by revolving the region enclosed by the graphs of $y=e^x$, $y=0$, $x=0$, and $x=1$ about the line $x=2$. Could you evaluate the integral?
Week 5
+
Find the volume of rotation of the region between $y=\sin x$ and $y=\cos x$, $0\leq x\leq \pi/2$ about the lines $x=\pi$ and $y=2$. Only set up the integral.
Evaluate the following integral: \[\int x\cos(3x+2)dx=\]
Evaluate the following integral: \[\int x^3\ln x dx=\]
Evaluate the following integral: \[\int xe^{x^2}dx=\]
Evaluate the following integral: \[\int \arctan x dx=\]
Evaluate the following integral: \[\int e^2\cos xdx=\]
Evaluate the following integral: \[\int \sin^4 x\cos xdx=\]
+
+
Formulas: \begin{align*} \sin A \cos B &= \frac{1}{2}(\sin(A+B)+\sin(A-B))\\ \cos A \cos B &= \frac{1}{2}(\cos(A-B)+\cos(A+B))\\ \sin A \sin B &= \frac{1}{2}(\cos(A-B)-\cos(A+B))\\ \sin (2A)&=2\sin A\cos A\\ \cos^2 A&=\frac{1}{2}(1+\cos(2A))\\ \sin^2 A&=\frac{1}{2}(1-\cos(2A)) \end{align*}
Compute the integral \[\int \sin(2x)\cos(3x)dx\]
Compute the integral \[\int \cos^2 (2z)dz\]
Compute the integral \[\int_0^{\pi/3} \sin^5 xdx\]
Compute the integral \[\int_0^\pi\sin^4 x dx\]
Compute the integral \[\int_0^{\pi/2}\cos(5x)\cos(x) dx\]
Evaluate the integral $\displaystyle \int_5^8\frac{3x-7}{x^2-5x+6}dx$.
+
Partial Fractions Decompositions: Every proper rational function can be written in the form \[\frac{p(x)}{q(x)} = \sum \frac{r(x)}{s(x)^n},\] where
- $s(x)$ is an irreducible factor of $q(x)$
- $n$ can be, a priori, any integer between 1 and the exponent of $s(x)$ in $q(x)$,
- $r(x)$ has degree $\lt$ the degree of $s(x)$.
Find the partial fraction decomposition, as well as the integrals, of the following rational functions:
- $\displaystyle \frac{x^2+x+1}{(x+1)(x+4)^2}=$
- $\displaystyle \frac{2x^3+x^2-x-1}{2x^2-x}=$
- $\displaystyle \frac{x-1}{x(x^2+1)}=$
Week 6
+
State whether each of the following integrals are improper or not. Find the values of all improper integrals below, and state whether they are convergent or divergent.
- $\displaystyle \int_{-1}^1\frac{1}{x^{2/3}}dx$
- $\displaystyle \int_{-\infty}^\infty\frac{1}{16+x^2}dx $
- $\displaystyle \int_0^\infty xe^{-x}dx $
+
Compute \[\int \frac{\arctan x}{x^2}dx=\]
- Is $\displaystyle \int_1^\infty \frac{\arctan x}{x^2}dx$ proper or improper? Compute it.
- Is $\displaystyle \int_0^1 \frac{\arctan x}{x^2}dx$ proper or improper? Compute it.
Compute the integrals \[\int \sin^2(2x)\cos(3x)dx\ \ \ \ \ \ \ \ \ \int_0^{\pi/4}\sin(2x+\pi/3)\cos^2(x)dx\]
Find the partial fractions decomposition of \[\frac{2 x^3 + x^2 + 2 x - 2}{x^2 (x^2 + 2)}=\]
Use integration by parts to compute the integrals \[\int_0^{\pi/4}x\sin 2x dx\ \ \ \ \ \ \ \ \ \int (\ln x)^2 dx\ \ \ \ \ \ \ \ \ \int_0^1 \frac{x^3}{\sqrt{9+x^2}}dx\] [Hint: For the last one try $u=x^2$.]
+
Estimate the area under the graph of $f(x)=e^{-x^2}$ over the interval $0\leq x\leq 2$.
+
Week 7
+
Trig Hobbit's Foyer is covered with a mat whose density is given by $\rho(x,y)=x^2+y+20$ kg/m2. Compute the total mass of the mat.
Give a sketch of the region $R=[-2,2]\times[-1,0]$ in the xy-plane and evaluate the double integral \[\iint_R(6x^2y+xe^y)dA.\]
Give a sketch of the region $R$ enclosed by $y=x^2$, $y=-x$, and $x=2$, in the xy-plane and evaluate the double integral \[\iint_R(6x^2y+xe^y)dA.\]
+
Find a parametrization of the region in the xy-plane enclosed by $y=x+1$, $y=x$, $x=0$, and $x=1$.
Find a parametrization of the region in the xy-plane enclosed by $y=x^2$ and $y=x(1-x)$.
Compute \[V=\iint_R (15-3x)dA\] where $R=[0,5]\times[0,3]$. Sketch the solid whose volume is represented by $V$.
Compute \[\int_1^2\int_1^3\frac{\ln(xy)dydx}{y}\]
Compute the double integral \[\int_1^2\int_0^x e^x dydx\]
+
Formulas: \begin{align*} x&=r\cos \theta\\ y&=r\sin \theta\\ x^2+y^2&=r^2\\ \frac{y}{x}&=\tan\theta \end{align*}
Convert the following rectangular coordinates to polar coordinates:
- $(3,-3)$
- $(2,\sqrt{3})$
Convert the following polar coordinates to rectangular coordinates:
- $(\sqrt{2},\pi/4)$
- $(2,7\pi/6)$
The density of a quarter of a disc of radius 2m centered at the origin sitting in the first quadrant is given by the function $f(x,y)=2x^2+y^2$ kg/m2. Find the total mass of the quarter disc in kg.
+
Formulas: \begin{align*} x&=r\cos \theta\\ y&=r\sin \theta\\ x^2+y^2&=r^2\\ \frac{y}{x}&=\tan\theta\\ dxdy&=rdrd\theta \end{align*}
The density of a quarter of a disc of radius 2m centered at the origin sitting in the first quadrant is given by the function $f(x,y)=2x^2+y^2$ kg/m2. Find the total mass of the quarter disc in kg.
A variety of deep sea worm is distributed about a hydrothermal vent according to the population density \[\rho(r,\theta)=\frac{8000\sin^2(\theta/2)}{9+r^2},\] thousand per sq. miles where $1 \leq r \leq 3$ is the distance (in miles) from the vent. Find the total population of the sea worm.
Solve for the general solution of the differential equation $y'(x) = 3x^2y$. Find the particular solution such that $y(0) = −2$.
Week 8
+
Solve for the general solution of the differential equation $y'(x) = 3x^2y$. Find the particular solution such that $y(0) = −2$.
An outbreak of zombies was discovered in the rural City of Sweet Water. The all embracing Mayor Dumass of the city believes that humans and zombies could coexist and wanted laws set up to stop (the still human) people in the city from an all out hunting spree. Renown scientist Dr Madd who survived a recent zombie attack has called for a City Council meeting to convince Mayor Dumass and all administrators of the serious dangers of an unchecked zombie population. Recent estimates give the number of zombies at one thousand and the total city population (both zombies and humans) at forty thousand. If zombie infection occurs at a rate of 0.1 thousand per day per one thousand human per one thousand zombie, how would scientitst Dr Madd convince the City Council that they need to act fast and hit hard on the zombie population before it is too late?
Newton’s Law of Cooling states that the rate of cooling of an object is proportional to the temperature difference between the object and its surroundings. A roast turkey is taken from an oven when its temperature is 185˚F and is placed on a table in a room where the temperature is 75˚F. Temperature of the turkey falls to 150˚F after half an hour. Apply Newton’s Law of Cooling to find the temperature of the turkey after 45 minutes.
+
What method should you use to evaluate each of the following integrals? \[\int_3^5\frac{2}{x^2-3}\] \[\int_{-1}^1\frac{2}{x^2}\] \[\int_{-\pi}^\pi\sin^2(x/4)\cos^3(x/4)dx\] \[\int_3^5\frac{2}{x^2+3}\] \[\int x\ln x dx\] \[\int_3^5\frac{2x}{x^2+3}\] \[\int_1^\infty xe^{-x}dx\] \[\int_{-1}^1\int_1^2 \frac{x}{y}dydx\]
Evaluate the double integral $\displaystyle\iint_D (2r+3\theta)dA$ over the region $D$ which is the portion of the circle of radius 2, centered at the origin, which lies in the 3rd quadrant.
Solve the differential equation \[\frac{dy}{dx}=\frac{1}{y}\]
Find a function $y=y(x)$, whose rate of change is proportional to $y+1/y$, knowing the initial condition that $y(1)=y'(1)=1$.
+
The Exponential Growth/Decay Model: \[\frac{dy}{dt}=ky\]
The Logistic Model: \[\frac{dy}{dt}=ky\left(1-\frac{y}{N}\right)\]
Write down an initial value problem for a population (in thousands) of fish growing exponentially with growth constant 0.5 and initial population 5 thousand.
A population of fish grows with growth constant (intrinsic growth rate) of 0.5 in a lake of carrying capacity 10 thousand is modeled by the logistic differential equation \[\frac{dp}{dt}=0.5p\left(1-\frac{p}{10}\right)\] where p is its population measured in thousands. If the initial population is 5 thousand, find a formula for p(t). What is the value of $\lim\limits_{t\to\infty}p(t)$?
Some scientists found that the fraction y(t) of species of fish in a lake is changing according to the model \[64\frac{dy}{dt}=-1-(y-1)^2\] where $0 \leq y \leq 1$ and t is in years. If the initial fraction of species in the lake is assumed to be at 1, solve for y(t). Explain from the model why the number of species is decreasing. How long will it take for the species of fish to completely disappear?
+
First order linear differential equations: \[y'+A(x)y=B(x)\] multiply by $\displaystyle \alpha(x)=e^{\int A(x)dx}$, satisfying $\alpha'=\alpha A$ and get \[(\alpha y)' = \alpha y'+\alpha A y = \alpha B\] which can be integrated.
Solve the initial value problem: $xy' + y = e^{2x}$ and $y(1) = 0$.
Solve the following equation using integrating factors: $y' − (\tan x)y = 1$, $y(0) = 3$, $-\pi/2\lt x\lt \pi/2$.
Solve the following equation using integrating factors: \[x\frac{dy}{dx}+5y=\frac{e^x}{x^3}.\]
Week 9
+
Solutions When modeling the change in concentration of a solution it's easiest to keep track of the quantity of the substance you are dissolving: \[Q'(t) = Q_{\operatorname{in}} - Q_{\operatorname{out}}\]
A tank contains 800 L of fresh water. Brine that contains 0.05 kg of salt per liter enters the tank at a tank at a rate of 40 L/min. Brine is drained from the tank at the same rate of 40 L/min. Find an expression for the amount of salt in the tank at any time t.
What if the brine in the previous problem is drained out at slower rate of 10 L/min? Find an expression for the amount of salt in the tank at any time t in this case.
+
For each of the following differential equations, which method would you use? If it's a separable differential equation, write the separated version. If it's a first order linear differential equation, compute the multiplication factor $\alpha$. (It might be both, in which case choose one thing to do.)
- $\displaystyle dy/dx + y = x$
- $\displaystyle y' + y = y^2$
- $\displaystyle \sqrt{x}y' + y/\sqrt{x}=1$
- $\displaystyle y\cdot y'=\sin x$
- $\displaystyle y' = 7-3y$
Set up a differential equation for the temperature $y(t)$ of a hot stone which is taken from boiling water and left at 70F room temperature. You may use Newton's law of cooling which states that the rate of change of temperature is proportional to the difference between the temperature of the object and that of the ambient space. If you're done with the other questions, try to solve the differential equation.
A tank with a capacity of 400 liters is full of a mixture of water and chlorine with a concentration of 0.05 grams of chlorine per liter. Chlorinated water with concentration of 0.01 grams of chlorine per liter is pumped into the tank at a rate of 4 liters per second. The mixture is kept stirred and is pumped out at a rate of 5 liters per second.
- Set up a differential equation satisfied by the amount of chlorine in the tank as a function of time.
- Solve the differential equation (but only if you're done with the other questions)
+
Euler's Method for Approximate Solutions to Linear Differential Equations \begin{align*}y'&=F(x,y)\\ y'(x) &= F(x, y(x))\end{align*}
- Start with an initial value $y(x_0)=y_0$ and change $x$ in increments of $\Delta x$.
- We'll approximate $y(x_0+\Delta x)\approx y(x_0)+y'(x_0)\Delta x$, where $y'(x_0)=F(x_0,y(x_0))$ from the differential equation.
- Keep going, to find $y(x_0+n \Delta x)$ using the approximation of the values of $y$ and $y'$ at $x_0+(n-1)\Delta x$.
- The smaller $\Delta x$ is, the better the approximations are.
+
Week 10
+
The weight w in kilograms of a kind of tropical fungus is modeled by the differential equation \[\frac{dw}{dt} =\frac{\sqrt{w}}{t^2+1};\ \ \ \ \ w(1) = 4.\] Here t denotes the time measured in weeks. Estimate the weight of the fungus at t = 2.5 weeks using Euler’s method with three steps.
Consider the height function of the hobbit house $f(x, y) = 14 − \frac{1}{100}(x^2 + y^2)$ over the given floor plan.
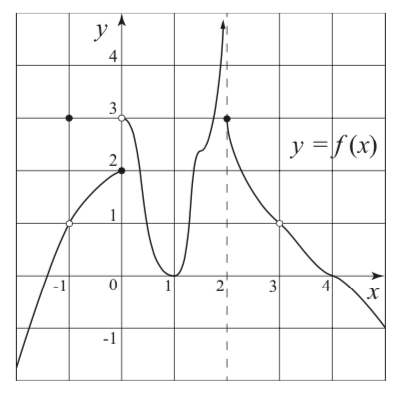
- When a hobbit climbs on the roof along y = 10, find how fast is his height f(x, y) is changing with respect to x.
- When y is arbitrarily fixed, find how fast f(x, y) is changing with respect to x.
- When x = 1, find how fast f(x, y) is changing with respect to y.
- When x is arbitrarily fixed, find how fast f(x, y) is changing with respect to y.
Find all first and second partial derivatives of the function \[g(x, y) = xe^{x^2y}.\]
+
Find all first and second partial derivatives of the function \[g(x, y) = xe^{x^2y}.\]
Compute the partial first derivatives of the function $h(x,y) = x^y$.
Compute all 4 partial second derivatives of the function $f(x,y) = 4x^2y+y^3$ and check that $f_{xy}=f_{yx}$.
The function $y(t)$ satisfies the differential equation $y'(t) = t^2-y$ with initial condition $y(3)=1$. Use Euler's method to estimate $y(3.3)$ using steps of size $\Delta t=0.1$.
Solve the differential equation \[y'+\frac{x}{x^2+1}y=\frac{1}{(1+x^2)^{3/2}}\] with initial condition $y(1)=0$.
+
Find formulas for the following derivatives by first drawing a tree diagram to connect all related quantities:
- $\frac{\partial u}{\partial t}$ where $u = \ln(x^2 + y^2)$, $x = \cos 2t$, and $y = \sin t$.
- $\frac{\partial u}{\partial t}$ and $\frac{\partial u}{\partial s}$ where $u = e^{x_1+4x_2−x_3}$, $x_1 = 2t − s$, $x_2 = t^2$, and $x_3 = t + 3s$.
+
You are given that $ze^{x+2y} + z^2 − x − y = 0$. Find $\dfrac{\partial z}{\partial x}$ and $\dfrac{\partial z}{\partial y}$.
Using linear approximation, estimate the change in $g(x, y) = xe^{x^2y}$ when (x, y) changes from (1, 0) to (0.9, 0.2). In other words, estimate the value g(0.9, 0.2) − g(1, 0).
+
Polar
coordinates
Mobius: 22.5, 22.8, 22.9, 22.10, 23.5, 23.6, 23.7
Double integrals
in cartesian coordinates
Mobius: 20.3, 21.6
Double integrals
in cartesian coordinates over general regions
Mobius: 20.4, 21.9, 22.7,
Double integrals
in polar coordinates
Mobius: 23.9, 24.8, 24.9
Separable
differential equations
Mobius: 22.2, 22.4, 22.6, 23.1, 23.3, 23.4, 24.2, 24.4, 25.3,
25.4, 26.2, 26.3
Separable
differential equations: the Logistic equation
Mobius: 23.10, 24.6
First order
linear differential equations
Mobius: 23.8, 23.11, 24.5, 24.5, 25.7
Week 11
+
Find $z_x =\dfrac{\partial z}{\partial x}$ and $z_y =\dfrac{\partial z}{\partial y}$ in each of the following expressions:
- $x^3yz=y^2+3x-2xz^3-7$ and compute $z_y(1,1,-1)$.
- $\displaystyle e^{yz}+\frac{1}{x+2z}=\frac{4}{3}$ and compute $z_x(1,0,1)$.
Compute the sensitivity and elasticity coefficients of the function $z = xy^2$ at $x=2, y=3$.
+
Calculate $\partial z/\partial x$ at $(3,2,\pm 1)$ where $z$ is defined implicitly by the equation $z^4+x^2z^2-y-8=0$.
You know that $x^2y+y^2z+xz^2=7$. What is the elasticity coefficient of $z$ with respect to $x$ at the point (1,1,2)?
Let $w=x^2\ln (x^2+y^2)$.
- If $x=e^{-t}$ and $y=\ln t$ find $dw/dt$ when $t=1$.
- If $x=e^{-t+s}$ and $y=t^2+2s$ find $\partial w/\partial s$ when $t=1, s=-1$.
Two slightly more challenging questions:
Compute $\dfrac{\partial u}{\partial t}$ where $u=x^2+y^3$, $x=e^{zw}$, $y=\ln w$, $z=2t+s$, $w=t+2s$.
You know that $x+y^2+xz^3=1$. What is $z_{xy}$ at the point (1,1,-1)?
+
You know that $x^2y+y^2z+xz^2=7$. What is the elasticity coefficient of $z$ with respect to $x$ at the point (1,1,2)?
Let $w=x^2\ln (x^2+y^2)$.
- If $x=e^{-t}$ and $y=\ln t$ find $dw/dt$ when $t=1$.
- If $x=e^{-t+s}$ and $y=t^2+2s$ find $\partial w/\partial s$ when $t=1, s=-1$.
A boundary stripe 3 inches wide is painted around a rectangle whose dimensions are 100ft by 200ft. Use linear approximation to estimate the number of square feet of paint in the stripe.
Consider the function $f(x, y) = cos(xy^3)$.
- Find the sensitivity coefficient of f(x, y) relative to x and the sensitivity coefficient of f(x, y) relative to y at the point (0.5, 1).
- Using linear approximation estimate the change in f(x, y) when (x, y) changes from (0.5, 1) to (0.4, 1.2). What is the estimated corresponding percentage change? Give your answer round to two decimal places.
- What the elasticity of f(x, y) relative to x and elasticity of f(x, y) relative to y at (0.5, 1)?
+
+
Separable
differential equations
Mobius: 22.2, 22.4, 22.6, 23.1, 23.3, 23.4, 24.2, 24.4, 25.3,
25.4, 26.2, 26.3, 23.10, 24.6
First order
linear differential equations
Mobius: 23.8, 23.11, 24.5, 24.5, 25.7
Euler's Method
Mobius: 25.8, 26.7, 27.1
Computing partial derivatives
Mobius: 27.6, 27.7, 27.8
Estimating Partial derivatives
Mobius: 27.4
Week 12
+
Lagrange Multipliers
The extremal values of $f(x,y)$ subject to
the constraint $g(x,y)=0$ are found either at the endpoints
of the curve $g(x,y)=0$ or at critical
points which satisfy
\begin{align*}
\frac{\partial f}{\partial x}&=\lambda \frac{\partial g}{\partial x}\\
\frac{\partial f}{\partial y}&=\lambda \frac{\partial g}{\partial y}\\
g(x,y)&=0
\end{align*}
Why is this reasonable?
Suppose you are at a point of min or max, and move a little,
say by $\Delta x$ in the $x$-direction and $\Delta y$ in the
$y$-direction.
- Because you are at a min or max, a small change in your position won't change $f(x,y)$ (for 1-variable this means horizontal tangent line at a max or min): \[0=\Delta f \approx \frac{\partial f}{\partial x}\Delta x+\frac{\partial f}{\partial y}\Delta y.\]
- Because you move along the path/curve $g(x,y)=0$, the value of $g$ stays constant: \[0=\Delta g \approx \frac{\partial g}{\partial x}\Delta x+\frac{\partial g}{\partial y}\Delta y.\]
What is the minimum value of $f(x,y)=x^2+y^2$ if $2x+4y =10$?
The height of the slanted roof a house is given $h(x, y) = 2x + 4y + 20$. A spider on the roof
is observed from the top view crawling on the closed path $x^2 + y^2 = 4$. What is the minimum and
maximum height attained by the spider?
In this context, the function we need to optimize is the height $h(x,y) = 2x + 4y + 20$ with constraint $x^2 + y^2 - 4=0$.
Can you roughly draw a picture to depict the path of the spider on the roof showing where the graph
of $x^2 + y^2 = 4$ is in relation to the actual path of the spider? Use Lagrange multipliers to find the
minimum and maximum heights of the spider.
How would you change your answer if the spider only crawled on the path that tracks the upper semi-circular part of the curve $x^2 + y^2 = 4$?
+
Find the general term of the following sequences, assuming that the pattern of the first few terms continues. Determine if they are geometric. Find also the limit of each of the sequence.
- $\displaystyle \left\{\frac{1}{2}, \frac{2}{3},\frac{3}{4},\frac{4}{5},\ldots\right\}$.
- $\displaystyle \left\{-\frac{4}{5}, \frac{8}{25}, -\frac{16}{125}, \frac{32}{625},\ldots\right\}$.
- $\displaystyle c_{n+1}=(n+1)c_n$ for $n\geq 1$ and $c_1=1$.
Find the limit of each of the following sequences, where $n = 1, 2, 3, \ldots$ if it exists.
- $\displaystyle b_n=\frac{1-e^{2n}+4e^{6n}}{5+5e^n+e^{6n}}$.
- $\displaystyle c_n=\cos(n\pi)$.
- $\displaystyle d_n=e^{-n}\sin(n)$.
+
+
Geometric Series \begin{align*} c + cr + cr^2 +\cdots + cr^{N-1} &= \frac{c(1-r^N)}{1-r}\\ c + cr + cr^2 + \cdots &= \frac{c}{1-r}\textrm{ if }|r|<1 \end{align*}
A ball is projected from the ground to a height of 10 feet and allowed to freely fall and rebound when it hits the ground. If the ball rebounds to 80% of the height it fell from and is allowed to continue its motion indefinitely answer the questions below.
- List the height attained by the ball just before it hits the ground the nth time for n = 1, 2, 3, and 4. Draw a picture to explain how you arrive at your answer. Identify any pattern you observed and write down he maximum height hn attained by the ball before it hits the ground the nth time. What is the limit of the sequence $\{h_n\}$?
- What can you say about the ratio of the consecutive terms $h_{n+1}/h_n$?
- Write out as a sum, the total vertical distance travelled by the ball when its hits the floor the first time, second time, third times and fourth time. If the bouncing persists, write down using summation notation the total distance travelled by the ball. Is the total vertical distance travelled by the ball finite or infinite? Make a guess.
If a chessboard were to have wheat placed upon each square such that one grain were placed on the first square, two on the second, four on the third, and so on (doubling the number of grains on each subsequent square), how many grains of wheat would be on the chessboard at the finish? (Statement and image from https://en.wikipedia.org/wiki/Wheat_and_chessboard_problem)

Find the total distance travelled by the ball in the first exercise.
Find the sum of the first 20 terms in the geometric series $\displaystyle \sum_{n=3}^\infty \frac{2^{2n}}{3^n}$. This is also called the 20th partial sum. What is the sum (to infinity) of the series.
Week 13
+
Geometric Series \begin{align*} c + cr + cr^2 +\cdots + cr^{N-1} &= \frac{c(1-r^N)}{1-r}\\ c + cr + cr^2 + \cdots &= \frac{c}{1-r}\textrm{ if }|r|<1 \end{align*}
Rewrite each of the following repeated decimals as a fraction.
- $0.\overline{9}=0.999999\ldots$
- $3.0\overline{12}=3.012121212\ldots$
A drug is designed so that 60% remains in the body at the end of each 24 hour period (one day). If 30 mg of the drug is given daily to a patient find
- the amount of drug in the body after 10 days before the next dose is given, and
- the approximate amount of drug in the body after a very long time assuming measurement is done before the next dose is given
Consider the series \[\sum_{n=5}^\infty(\sqrt{n+1}-\sqrt{n}).\]
- Find the sum of the first 51 terms in the series.
- Is the series convergent?
Consider the series \[\sum_{k=0}^\infty\frac{2}{k^2+7k+12}.\]
- Apply partial fraction decomposition to the rational function $\displaystyle \frac{2}{k^2+7k+12}$.
- Compute $S_{49}$.
- Find $S_N$, N the Nth partial sum of the given series.
- Is the given series convergent? (It is.) Find the value of the given series.
+
Write the following series in summation notation \[\frac{125}{9}+\frac{625}{16}+\frac{3125}{25}+\frac{15625}{36}+\cdots\]
Compute the sum \[\sum_{n=0}^\infty\frac{3(-2)^n-5^n}{8^n}\]
Find the sum \[\frac{1}{1\cdot 3}+\frac{1}{3\cdot 5}+\frac{1}{5\cdot 7}+\cdots\]
Write $21.217217217217\ldots$ as a fraction.
A and B take turns flipping a fair coin, starting with A. The first to flip heads wins. How likely is it that A wins the game? [Hint: Write out the list of flips that guarantee a win for A.]
+
Convergence Criterion
\[S=\sum_{n=0}^\infty a_n\ \ \ \ \ \ \rho=\lim_{n\to\infty} \frac{a_{n+1}}{a_n}\]
- If $|\rho|\lt 1$ the series converges (absolutely)
- If $|\rho|\gt 1$ the series diverges
- If $|\rho|=1$ the test is inconclusive
Radius of Convergence
A power series
\[f(x)=\sum_{n=0}^\infty a_n (x-c)^n\]
has radius of convergence $r$ if
- the series $f(x)$ converges (absolutely) if $|x-c|\lt r$ and
- the series $f(x)$ diverges when $|x-c|\gt r$
+
Taylor expansion \[f(x)=a_0+a_1(x-c)+a_2(x-c)^2+\cdots\] where $a_0=f(c)$, $a_1=f'(c)$, $a_2=f''(c)/2!$, ..., $a_n = f^{(n)}(c)/n!$. \[f(x)\approx T_n(x)=f(c)+f'(c)(x-c)+\frac{f''(c)}{2!}(x-c)^2+\cdots+\frac{f^{(n)}(c)}{n!}(x-c)^n.\]
Find the Taylor Series centered at $x = 0$ for $f(x) = e^x$. What is the interval of convergence for this power series?
Using the Maclaurin polynomial $T_4(x)$ for $e^x$, estimate $e^{0.2}$.
Write down the error of your estimate for $e^{0.2}$ in the previous question as a series. Explain your answer.
+
Partial derivatives
Computations: 27.6, 27.7, 27.8, 28.5, 32.6
Estimates: 27.4, 28.4, 30.2, 30.3, 31.7
Limits: 30.6, 30.7, 32.3, 32.4
Multivariable Chain Rule
Chain rule: 28.7, 28.8, 28.9, 32.5
Implicit differentiation: 29.5, 29.6, 30.4, 30.5, 31.1,
31.3, 33.2
Linear Approximation
Estimating change: 29.2, 29.3, 29.4, 32.12, 32.13, 32.14
Sensitivity and elasticity: 30.3, 31.7, 30.1, 30.8, 31.2,
31.8, 34.9
Bonus Quiz 01
Method of Substitution: 28.3, 29.9
Mass: 28.1, 30.9, 31.4, 31.5, 31.6, 33.1
Volumes: 28.2, 29.8, 31.9, 31.10, 32.1, 32.2, 33.6, 33.7, 33.8
Work: 29.1
Week 14
+
+
Compute $T_3(x)$ for $f(x)=\sqrt{1+x}$ and use it to find an approximation for $\sqrt{1.1}$.
Do the following series converge? Use the ratio test.
- $\displaystyle \sum_{n=5}^\infty\frac{n^3}{5^n}$
- $\displaystyle \sum_{n=1}^\infty\frac{2^n+4^n}{7^n}$
- $\displaystyle \sum_{n=5}^\infty\frac{n!}{n^n}$
Which function has the Maclaurin series $\displaystyle \sum_{k=0}^\infty \frac{(-1)^k}{3^{k+1}}(x-3)^k$? For which values of $x$ is the expansion valid?
What is $\displaystyle \sum_{n=0}^\infty \frac{(\ln 5)^n}{n!}$?
+
Find the 3rd Taylor polynomial for the function $\ln(x + 2)$ centered at −1, and estimate $\ln(0.8)$.
Using the Taylor series for $\dfrac{1}{1 + x^2}$ centered at $x = 0$ and differentiation, find the Maclaurin series for $\dfrac{2x}{(1 + x^2)^2}$.
Remember that $\arctan' x = \dfrac{1}{1 + x^2}$.
- Using the Taylor series for $\dfrac{1}{1 + x^2}$ centered at $x = 0$ and integration, show that the Taylor series for $\arctan x$ at 0 is: \[\arctan x =\sum_{k=0}^\infty (−1)^k \frac{x^{2k+1}}{2k+1}\] for $− 1 \lt x\lt 1$.
- Write down the 7th Taylor series for $\arctan x$ at 0. Estimate the value of $\arctan(0.5)$. Write down the error for the estimate you found as an infinite series using summation notation.
- Write down the Taylor series for $f(x) = \arctan(1 − x)$ centered at 1, giving the values of x for which the series is convergent.
+
Find the 3rd-degree Taylor polynomial of $y(t)$ centered at zero, where $y(t)$ is the solution of the initial value problem \[y'= y^2 + ty, y(0) = −1.\] Use your result to estimate y(0.3).
Find the 3rd-degree Taylor polynomial of $y(t)$ centered at 1, where $y(t)$ is the solution of the initial value problem \[y'= y^2 + ty, y(1) = −1.\] Use your result to estimate y(0.8).
Augmentin dosage is 500mg every 12 hours. About 50% of the dose excreted and the half-life in the body is 1.3 hours. How much Augmentin is there in the body right before the last of 20 pills is taken? (https://www.accessdata.fda.gov/drugsatfda_docs/label/2008/050564s051lbl.pdf)
Consider the series $\displaystyle \sum_{k=4}^\infty \ln\left(\frac{2k-1}{2k+1}\right)$.
- What is $S_{100}$, the 100-th partial sum?
- What is $S_{N}$, the N-th partial sum?
- What is the value of the series?
What is the limit of the sequence $\displaystyle a_n=\frac{(2n+3)^3}{n^3+2^3}$?
+
Linear Approximation
Estimating change: 29.2, 29.3, 29.4, 32.12, 32.13, 32.14
Sensitivity and elasticity: 30.3, 31.7, 30.1, 30.8, 31.2,
31.8, 34.9, 38.9
Sequences
Algebra: 32.8, 32.9, 33.9, 35.2, 35.3, 36.3, 36.4
Limits: 33.3, 33.4, 33.5, 34.1, 34.2
Geometric sequence: 33.10, 34.3, 34.4
Geometric
series
Summation and convergence: 32.10, 32.11, 35.6, 36.2, 36.6
Applications of geometric
series
Decimals: 34.5, 35.5
Drugs: 34.8, 36.1
Telescoping
series
Mobius: 35.8, 35.9, 36.5, 36.6, 37.6, 38.1
Bonus Quiz
02
Integration by Parts: See older homeworks
Trig integrals: See older homeworks
Work: 22.3, 25.6, 29.1, 36.7-11
Week 15
+
The radius $y(t)$ of a circular patch of oil slick due to an oil spill in the ocean is modeled by the differential equation: $y' = 3ty + y^2$. Suppose the radius of the oil slick is 1 km when an hour after it was first observed.
- Compute the 3rd-degree Taylor polynomial for $y(t)$ at $t = 1$.
- Estimate the radius of the patch of oil when $t = 1.5$ using (1)
The population density of a town measured from the town square is given by the polar function $\displaystyle \rho(r, \theta) = \frac{\theta}{1 + r^4}$ where r is distance in kilometers, and $\rho(r, \theta)$ is in thousands per sq. km. Find the total population within a 3-km radius from the town square.
Solve the initial value problem: $y' = y +\frac{1}{1 + 2e^{−x}}$, $y(0) = 3$.
. The number of cellphones (in millions) owned by the residents of a city is given by the equation \[\frac{dy}{dt} = ye^{−t}; y(0) = 1,\] where t is the time in years from 2006.
- Use Euler’s method with $\Delta t = 2$ to estimate the number of cellphones owned in the year 2010.
- Solve exactly the initial value problem and compare to part (1)
The Taylor series of $\sin(2x)$ centered at $x = 0$ is given by $\displaystyle \sum_{n=1}^\infty (−1)^{n−1}\frac{2^{2n−1}}{(2n-1)!} x^{2n−1}$. Estimate the value of $\sin(0.4)$ using the 5th Taylor polynomial of $\sin(2x)$. Give the error of your estimate as a series.
Consider the series $\displaystyle \sum_{n=1}^\infty \frac{(x − 2)^n}{5^{2n}n^2}$. Find the value of x for which the series converges. You do not need to discuss convergence at end-points. State also the radius of convergence.
+
+
Derivatives
All rules for computing derivatives including power rule,
product rule, quotient rule, chain rule, logarithmic
differentiation. Types of functions would cover polynomials,
rational functions, exponential, logarithmic functions,
trigonometric functions and inverse trigonometric
functions.
Algebra: FR3.2
Computations/tangent lines/linearization: FR1.1, FR1.3, FR3.10
Exponential growth/decay: FR1.4, FR3.11
Applications of Riemann sums
Area between curves: FR1.5(a), FR2.17
Volume of solids with uniform cross-section: FR1.5(c),
FR1.9, FR3.14
Solid of revolution: FR1.5(b), FR2.10, FR3.16
Total mass/population: FR1.2, FR2.1, FR2.25, FR3.7
Work done: FR1.7, FR1.20, FR1.24, FR2.20, FR3.25
Integration
General: FR1.14(a)
Method of substitution: FR1.14(c,e), FR1.16, FR2.12
Integration by parts: FR1.14(g,h), FR2.8, FR3.9
Partial fraction decomposition: FR1.13(a), FR1.14(i),
FR2.2, FR3.24
Improper integrals: FR1.16
Trig integrals: FR11(b), FR1.14(b,d,f), FR2.11, FR2.21, FR3.13
Numerical integration: FR1.15(b), FR2.23, FR3.1
Separable
Equations.
Equation: FR1.6, FR11(a), FR2.24, FR3.22
Models: FR1.27, FR1.28, FR3.3, FR3.4, FR3.10
First Order Equations
Linear First Order Equations: FR1.26, FR2.16, FR3.18
Mixing tank problems: FR1.21, FR2.13
Euler's
Method.
FR1.22, FR2.7, FR3.6
Double integrals
Double integrals in both Cartesian coordinates: FR1.8,
FR3.15, FR3.19
Double integrals in polar coordinates: Fr1.2, FR2.19, FR3.7
Partial derivatives
Partial derivatives: FR2.3
Estimating partial derivatives from a table of values:
Mobius 27.4, 28.4, 30.2, 30.3, 31.7
Linearization
Linearization of two variable functions: Mobius 29.2, 29.3, 29.4, 32.12, 32.13, 32.14
Percentage change and elasticity: Mobius 30.3, 31.7, 30.1,
30.8, 31.2, 31.8, 34.9, 38.9
Sequences and series
Limits of sequences: FR1.18
Geometric sequences and geometric series: FR1.12, FR2.14
Telescoping series: FR1.13(b), FR2.4, FR3.8
Application of geometric series for repeated decimals and
drug dosages: FR1.23, FR2.18
Convergence of series
Ratio Test/Interval of convergence: FR1.25, FR2.15, FR3.17
Taylor
series
Taylor series and polynomials: FR1.15(a), FR1.17, FR2.5,
FR2.6, FR3.5, FR3.20, FR3.23
Applications to differential equations: FR1.10, FR2.22,
FR3.21