Math 43900 Problem Solving Lecture 1 Exercises

Exercise 1: Coins problem.

Exercise 2: Rabbitagoras.

Exercise 1: Three fleas sit on a line, not all in the same position. A flea can jump over another flea, landing on the other side in such a way that the fleas are half as far as they were. Show that the fleas can cooperate to jump arbitrarily far on the line. [Special case of IMO 2000 problem 3.]

Exercise 2: The Fibonacci sequence is defined by $F_0=F_1=1$ and $F_{n}=F_{n-1}+F_{n-2}$ for all indices $n\geq 2$. The first terms are $1,1,2,3,5,8,13,21,\ldots$. How many digits does $F_{1000,000}$ have? [I was asked this during a hedge-fund interview.]

Exercise 3: Find a smooth function $f(x)$ such that \[2xf'(x)+(x^2+9)f''(x)=0\]

Remark

Exercise 1: Consider the equation \[(x-1)(x-2)(x-3)(x-4) = (x-1)(x-2)(x-3)(x-4)\] What is the smallest number of linear factors that can be erased such that the resulting equation has no real solutions?

Exercise 2: Does the equation $x^2+x = 3^y$ have any integer solutions?

Exercise 3: Color each point of the plane with one of two colors. Show that there exists an equilateral triangle all of whose vertices have the same color. Do there exist infinitely many such triangles?

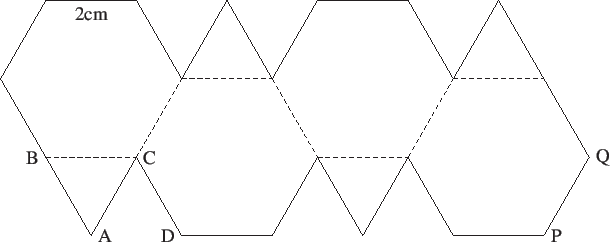
Exercise 4: What is the volume of the polyhedron you get if you fold the following diagram? [VTRMC 2015]