Notes on VTRMC 2017

I began by sketching very roughly the graphs of the functions on the two sides of the equation. I saw the LHS was defined between $\pm \sqrt{2}$ and had maximum $\sqrt{2}$. The RHS had a single root $\sqrt[3]{3}$ and the $y$-intercept was at $y=\sqrt[3]{3}$. The first question was which of $\sqrt{2}$ and $\sqrt[3]{3}$ was bigger but as $2^3<3^2$ it's the latter.

Also because $x^3$ is increasing, $3-x^3$ and therefore also the RHS are decreasing. The a rough graph is:
and the main question is what happens in the circled area, as it's clear what's going on outside the first quadrant.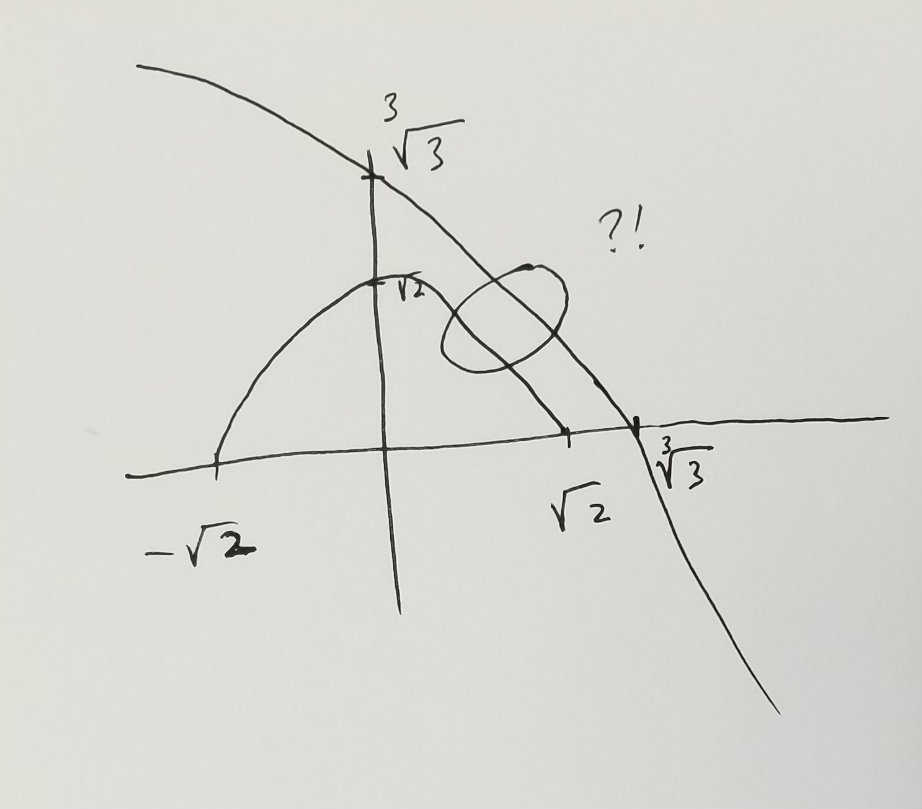

So how do you figure out what happens in the first quadrant? If you try to eliminate the roots you have to do way too many computations. You could look at RHS-LHS and try to minimize using calculus, but that looked nasty too.

What I tried was a trig substitution instead. On the LHS write $x=\sqrt{2}\cos u$ which will make the LHS equal to $\sqrt{2}\sin u$, the idea being that in the first quadrant both $\sin u$ and $\cos u$ are positive.

Now you can cube to compare $2\sqrt{2}\sin^3 u$ and $3-2\sqrt{2}\cos^3 u$ so we just need to figure out if $f(u)=\sin^3 u + \cos^3 u$ takes the value $\dfrac{3}{2\sqrt{2}}$ and count how often. But $f'(u) = 3\sin u\cos u (\sin u - \cos u)$ so the only critical point in $(0,\pi/2)$ (the first quadrant) is $u=\pi/4$. The function decreases from $u=0$ where $f(0)=1$ to $u=\pi/4$ where $f(u) = 1/\sqrt{2}$ and then increases back to $f(\pi/2)=1$. In particular $f(u)$ can never be $\dfrac{3}{2\sqrt{2}}>1$.
I tried a few things but really I had no idea how to do this problem.
My first reaction was: are you kidding me, plane geometry? That basically never happens on the Putnam. My second reaction was: seriously, weird angles? Back in 2001 at the International Math Olympiad I spent more than an hour getting nowhere with a similar problem, granted with weirder angles. So I was off to a bad start with this problem, but I figured since I failed so badly at the calculus problem I should at least draw the picture. Here is my first try.
Then I remembered what I repeated so often in class, namely to use some common knowledge to start. This problem is one of 7 to be done in 2.5 hours, so it can't be as elaborate as the IMO problem, which is 3 problems in 4.5 hours. Practically, this meant that the angle had to be something sensible, and the picture above suggested $45^\circ$. I scribbled some things on my picture so I drew another one, but on this second one the angle seemed more like $60^\circ$, so I decided to make a more accurate picture.

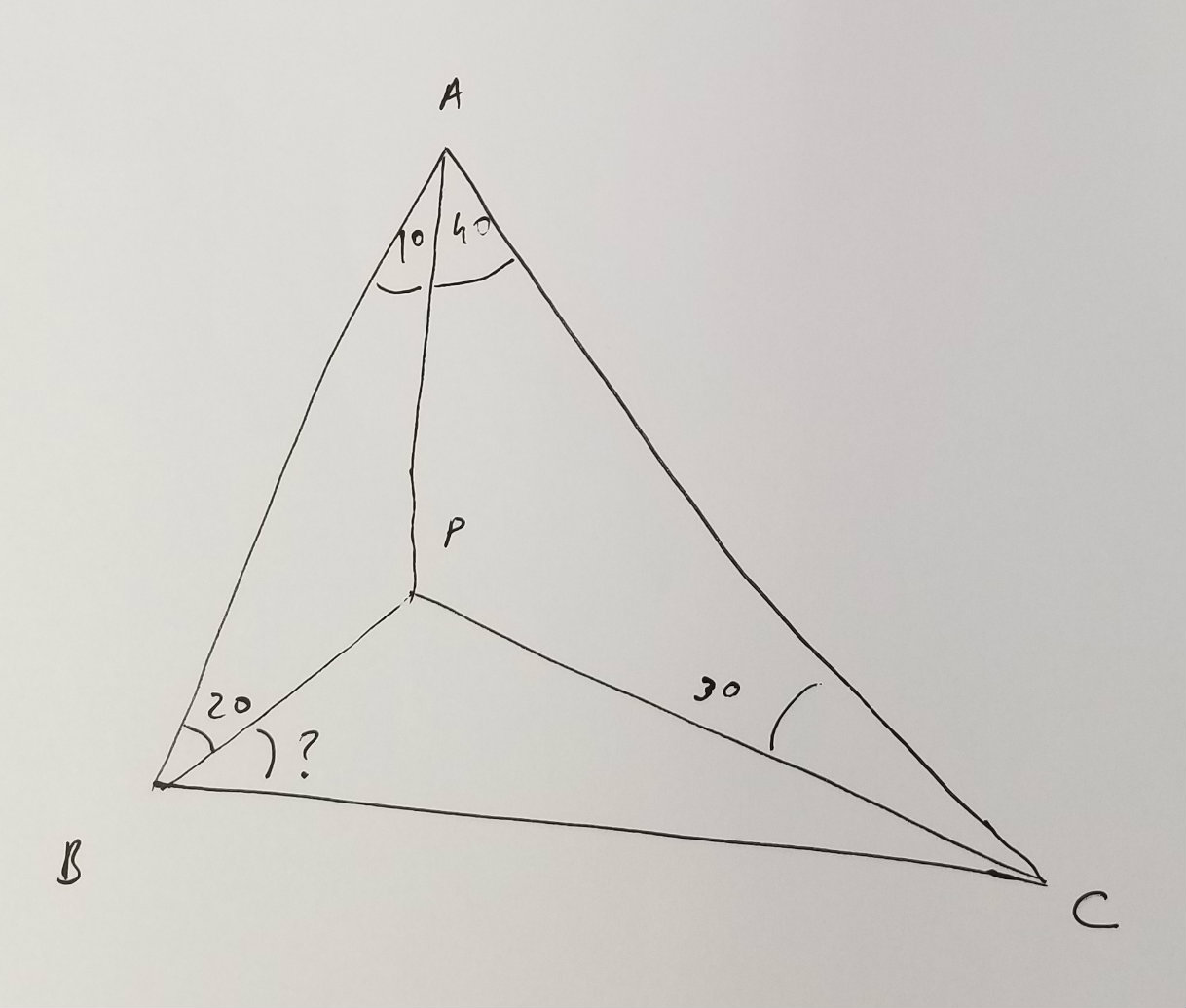
I can't draw a $40^\circ$ angle, but I can draw a $30^\circ$ angle. So I started off with an isosceles triangle $OAC$ with $30^\circ$ angles. Then next to one of the acute angles I drew what seemed to me a $10^\circ$ angle (I imagined trisecting the $30^\circ$. This gave me the ray $AP$ forming a $40^\circ$ angle with $AC$ and I drew $P$ at the intersection of the ray $AP$ and the line $OC$. Then another $10^\circ$ angle gave me the ray $AB$ and I placed the point $B$ on this ray where it seemed to me that $\angle ABP=20^\circ$. Now I was persuaded that $\angle PBC$ should really be $60^\circ$.
Once I had my guess I tried to figure out what implications my guess might have. It's amazing how often a correct guess can reveal how to solve a problem. So I computed all the angles in the picture assuming my guess.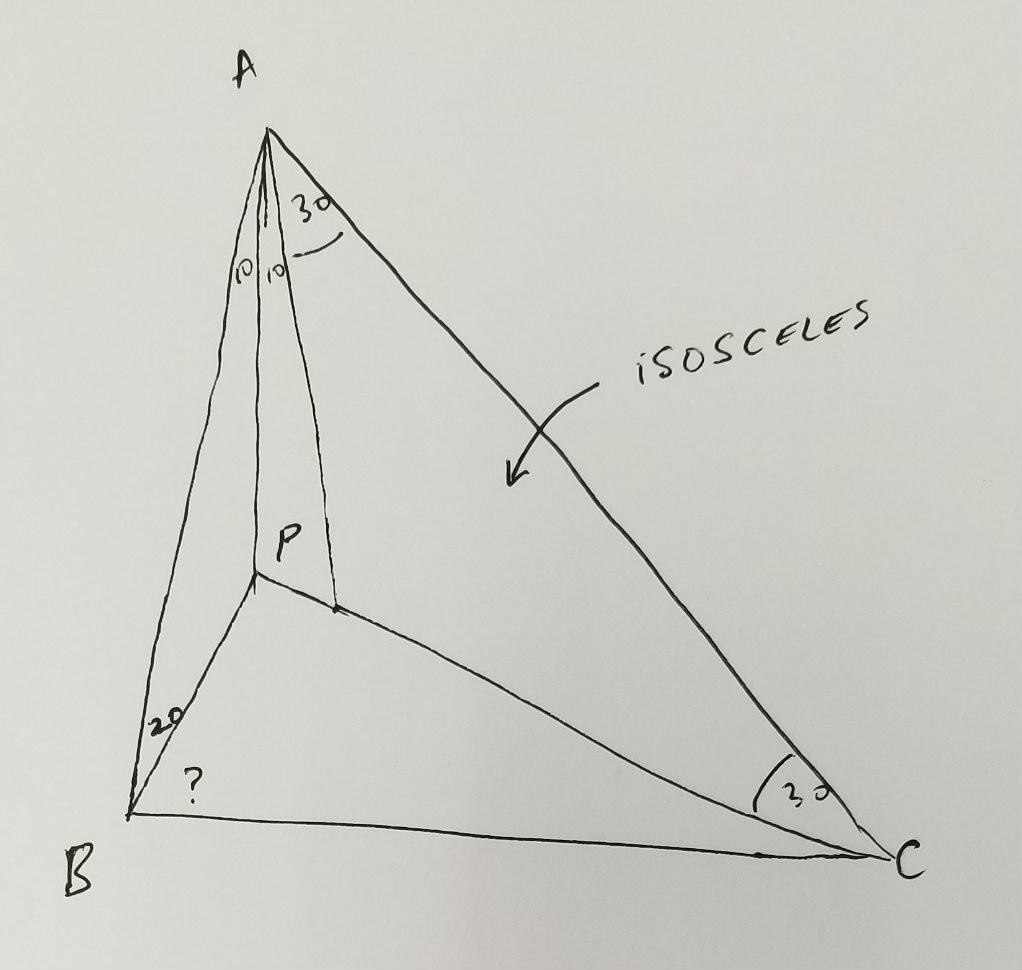
My conclusion was that if my guess is correct then $ABC$ would have to be isosceles, seeing how it had two angles of $50^\circ$. Then I tried to reverse engineer the problem. I noticed that my observation was an if and only if, i.e., if $BAC$ was isosceles then $\angle PBC=60^\circ$.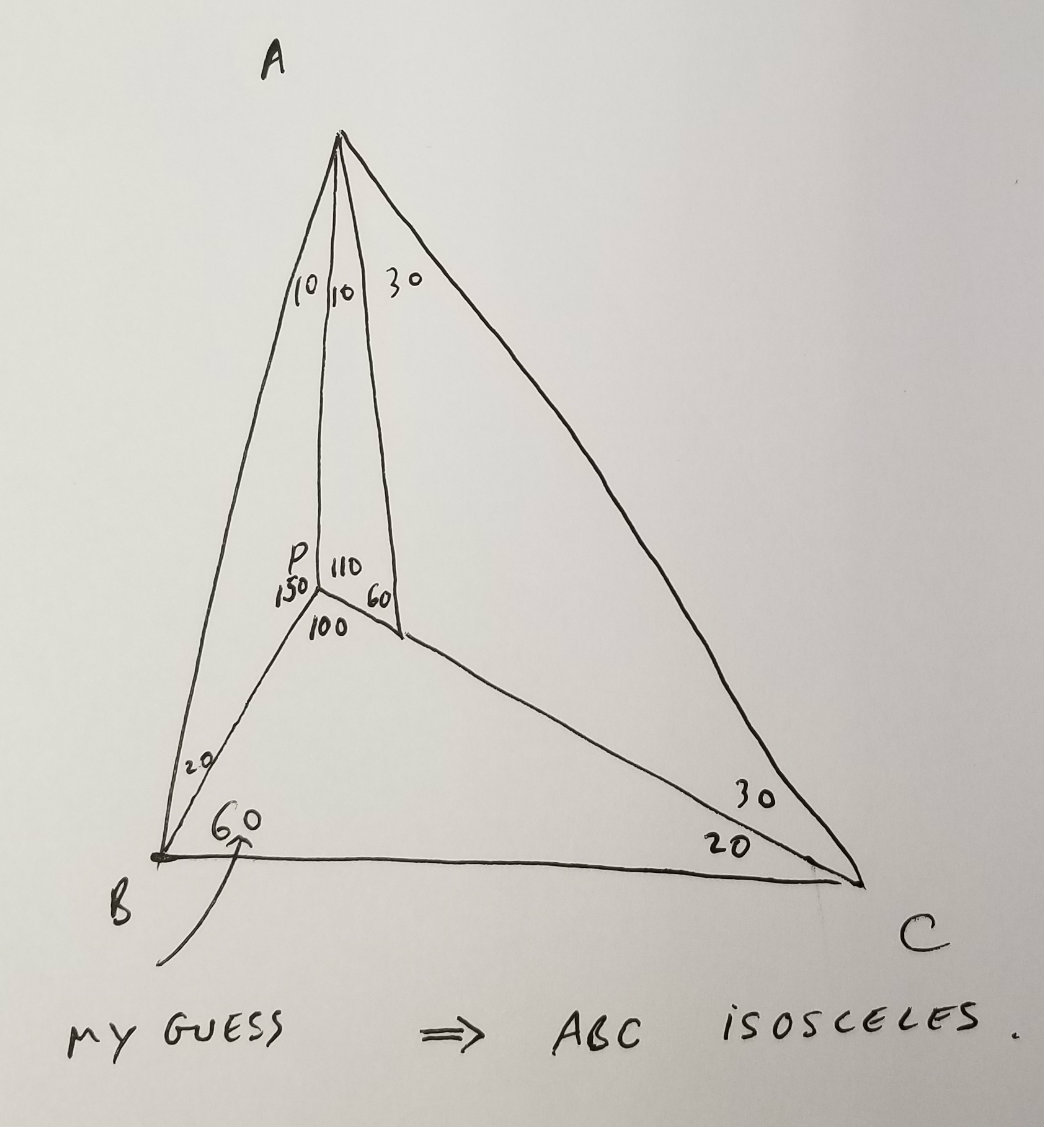

I can't draw a $20^\circ$ angle but I can draw an isosceles triangle so I tried to flip the construction. My original isosceles triangle $OAC$ is determined by the problem, and then $P$ is also determined, as is the ray $AB$. There is a unique placement of the point $B$ on the ray $AB$ where the angle $ABP$ is $20^\circ$ and there's a unique point $B'$ which makes $B'AC$ isosceles. What I decided to do is to draw the point $B'$ and then show directly that $\angle AB'P=20^\circ$ which would then give that $B=B'$ which is what I was after.

To do this I knew that $B'$ (inconveniently I wrote $B$ instead of $B'$ on the picture here) and $O$ would be on the line perpedincular to $AC$ through its midpoint so I simply drew that height:
Then I computed angles again and I noticed that there's two $10^\circ$ angles at the top around $A$ and two $60^\circ$ angles around $O$. But then $P$ would be the intersection of two bisectors in the triangle $AB'O$ and so the third bisector would pass through $P$ as well. Therefore $\angle AB'P=\angle PB'O$ is half of $\angle AB'O=40^\circ$ as desired.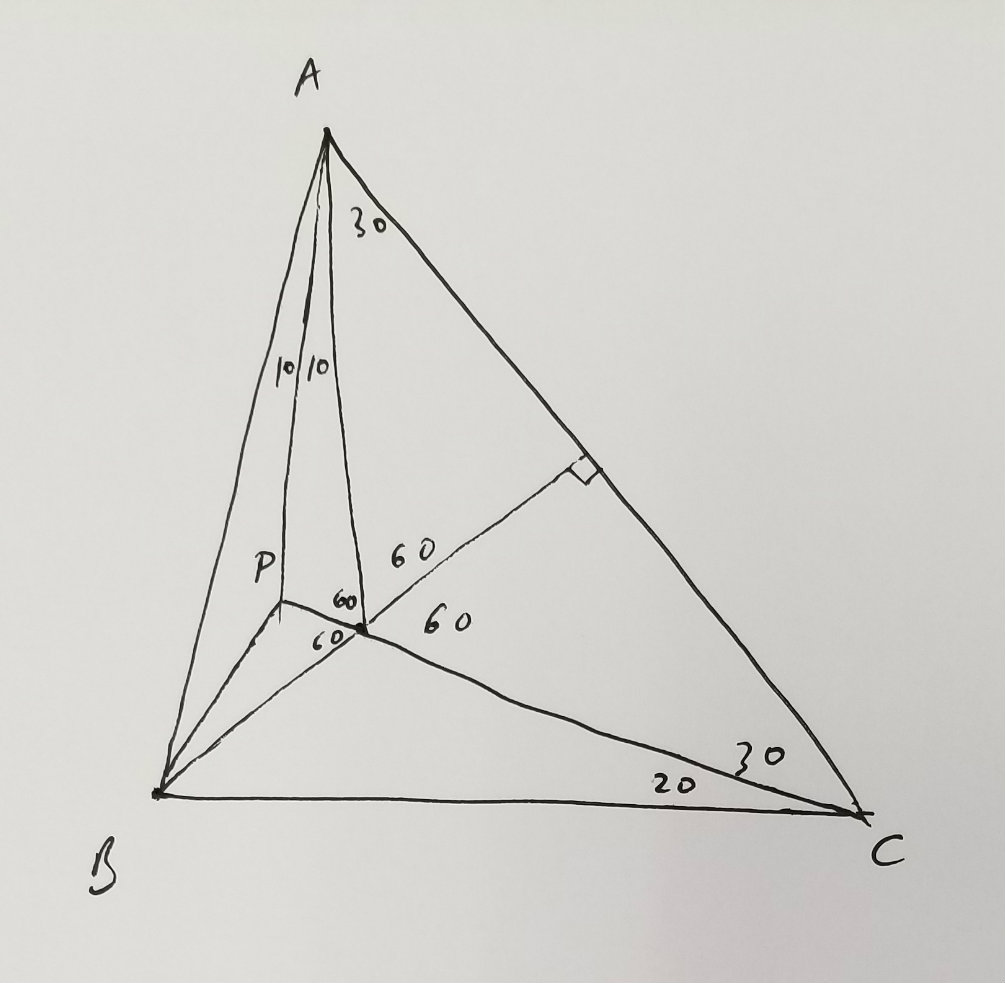

With this in hand I knew $B=B'$ and so $\angle BCA=\angle BAC=50^\circ$ which, after some angle chasing, gave $\angle PBC=60^\circ$.
This problem was the one that took me least to do because it so resembled the rabbit Pythagorean example I showed in my first lecture. The main idea there was that area varies quadratically so we were able to reduce the statement about the areas of the three rabbits to the usual Pytagorean theorem.

I draw the picture and noticed that the three triangles were all similar to the original one, being determined by parallel lines and therefore having the same angles.
Therefore to compute $a,b,c$ I just needed the scaling factors. If they are $s_a,s_b,s_c$ then I knew that $a/T = s_a^2$, and so on. The identity I needed to show then became \[s_a + s_b + s_c=1\] which conveniently had no square roots.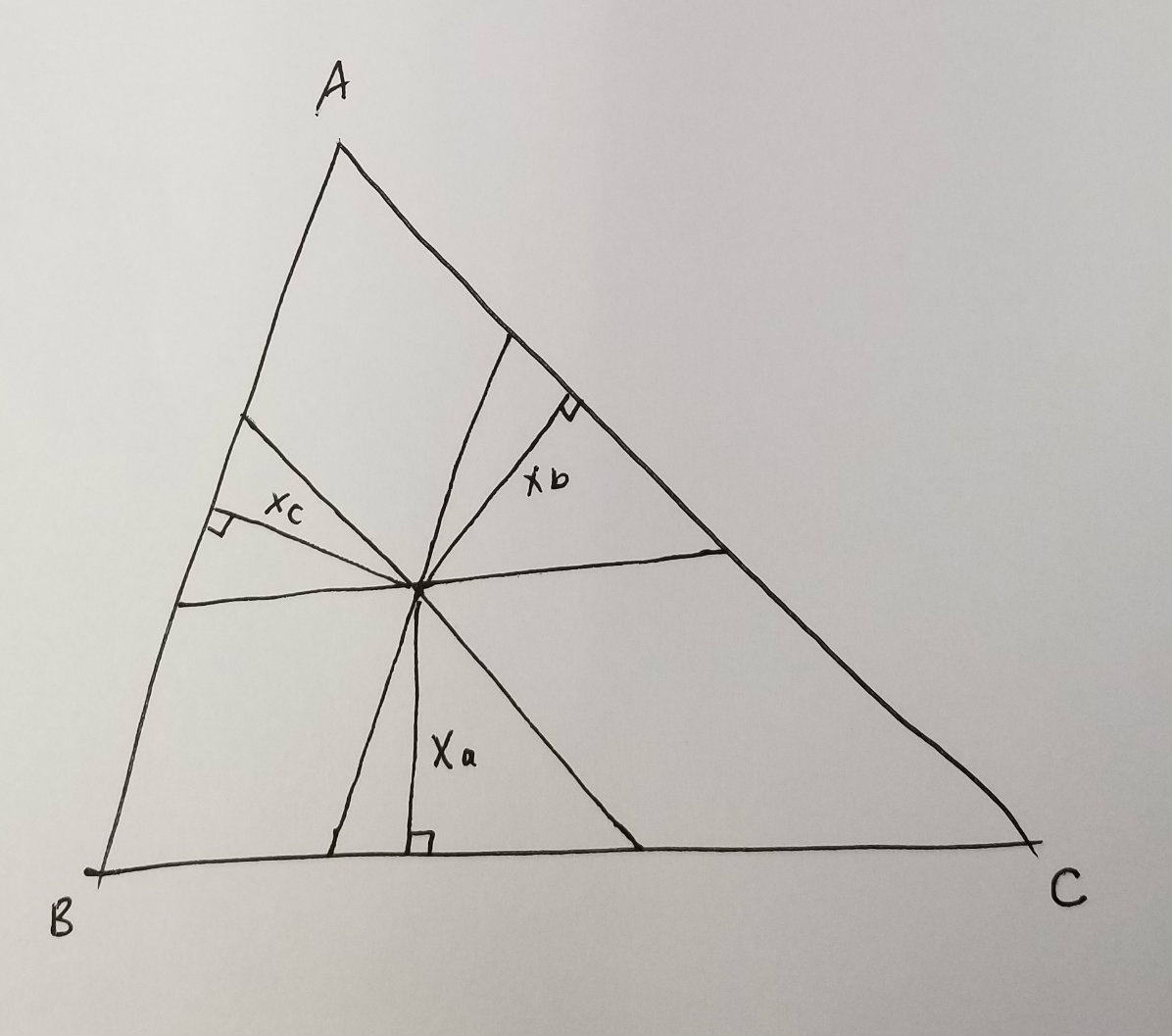

So how do you figure out these scaling factors? Well, they are scaling factors, so you can compute it as the ratio of any similar lengths. I decided to go for heights. Writing $h_a,h_b,h_c$ for the heights of the big triangle $T$ and $x_a,x_b,x_c$ for the corresponding (similar) heights in the three smaller triangles then $s_a=x_a/h_a$ and so on. The identity to show became \[\frac{x_a}{h_a}+\frac{x_b}{h_b}+\frac{x_c}{h_c}=1\] which made me a little worried because, well, it's been a while since I played around with plane geometry.

Again I remembered that this problem has to be doable among 7 in 2.5 hours so it really can't rely on some complicated plane geometry formulas.

What I noticed, and here I used my experience with plane geometry, was that there's a simple way to rewrite $x_a/h_a$ using that the area of a triangle is height times base over 2. I needed to find a common base though, and this common base was $BC$. Then \[\frac{x_a}{h_a} = \frac{x_a\cdot BC/2}{h_a\cdot BC/2} = \frac{area(PBC)}{area(ABC)}.\] Once I got here the rest was quick: I only needed to show that \[\frac{area(PBC)}{area(ABC)}+\frac{area(PAC)}{area(ABC)}+\frac{area(PAB)}{area(ABC)}=1\] in other words \[area(PBC)+area(PAC)+area(PAB)=area(ABC)\] but this is clear from the picture.
I recognized $f$ as being the arithmetic mean, $g$ as the geometric mean, and $h$ as this weird harmonic mean. The harmonic mean is not as well known as the other two, but it's supposed to be the inverse of the mean of the inverses, not particularly important. I did know that for all positive reals: \[f(x,y)\geq g(x,y)\geq h(x,y)\] and this you can do with algebra directly, the case of equality occurring when $x=y$. It turned out this wasn't particularly helpful because $a\neq b$ in the definition of $S$, so essentially I wasted five minutes.

Then I remembered that $a,b$ and all of $f(a,b)$, $g(a,b)$ and $h(a,b)$ are integers and square roots of integers are rarely integers, you need perfect squares! And you can characterize perfect squares even you look at their prime factorizations, all exponents have to be even.

So I wrote $d=(a,b)$ for the gcd and then $a=dA$, $b=dB$ with $A$ and $B$ coprime. Then $g(a,b)=\sqrt{ab}=d\sqrt{AB}$ has to be an integer and this can only happen when $AB$ is a perfect square. But $A$ and $B$ are coprime so, just by looking at their prime factorizations, each of $A$ and $B$ had to be a perfect square. So I wrote $A=u^2$ and $B=v^2$ and so $a=du^2$ and $b=dv^2$ and $a\neq b$ became $u\neq v$.

I also needed $f(a,b)=\dfrac{d(u^2+v^2)}{2}$ and $h(a,b) = \dfrac{2d u^2 v^2}{u^2+v^2}$ to be integers. Now I was getting somewhere, because you see $u$ and $v$ had to be coprime so $u^2$ had to be coprime to $u^2+v^2$ and $v^2$ had to be coprime to $u^2+v^2$. But then $h(a,b)$ is an integer ONLY if $u^2+v^2\mid 2d$.

To minimize $f(a,b)$ I needed to make $d$ as small as possible and $u^2+v^2$ as small as possible. Since $u\neq v$ are positive integers, the smallest value of $u^2+v^2$ is $2^2+1^2=5$. Then I need $5\mid 2d$ so $d$ is divisible by 5, and also $5d$ to be even so $d$ is at least 10. When the smallest values are attained then $u=2,v=1,d=10$ so $f(a,b)=25$.

It remained to show that 25 was the smallest possible value that could occur. Honestly, I stopped thinking about the problem once I got here, this is the advantage of not having to write a clean complete solution. But how would I have done it? Well, $u^2+v^2\mid 2d$ so $d$ is at least $(u^2+v^2)/2$ and so $f(a,b)\geq (u^2+v^2)^2/2$. But if $(u,v)\neq (2,1)$ then, since $u\neq v$, $u^2+v^2\geq 3^2+1^2=10$ and so $f(a,b)\geq 10^2/2 = 50$.
This is one problem where my experience as a problem solver showed me the way to do the problem, but I simply got lucky that I had this approach in my baggage of approaches.

The idea is that if $a$ and $b$ are integers then $a-b\mid a^k-b^k$ for any nonnegative integer $k$. (Just factor the RHS.) If you take linear combinations of $a^k-b^k$, say with coefficients $m_k$ then you get that \[a-b\mid \sum m_k(a^k-b^k)=\sum m_k a^k - \sum m_k b^k = f(a)-f(b)\] where $f(x)=\sum m_k x^k$ is the given polynomial.

The rest of the problem is then a series of manipulations of this idea. Indeed: \[n-1\mid f(n)-f(1) = n^2-4n-17\] \[n-4\mid f(n)-f(4) = n^2-4n-20\] \[n-8\mid f(n)-f(8) = n^2-4n-52\] Eg the first one gives \[\frac{n^2-4n-17}{n-1} = n-3-\frac{20}{n-1}\in \mathbb{Z}\] so $n-1\in \{\pm 1, \pm 2, \pm 4, \pm 5, \pm 10, \pm 20\}$. Going through the list one by one to see which value of $n$ satisfies the other two divisibilities yields only $n=3$ and $n=6$ as possibilities.
This problems was the hardest from my point of view. Here's how I started. From the equation $m\mid 2\cdot 3^n$ so $m$ is either of the form $3^k$ or of the form $2\cdot 3^k$ for some integer $0\leq k\leq n$ so essentially we have to solve the following equations: \[3^k + 2\cdot 3^{n-k} = 2^{n+1}-1\] \[2\cdot 3^k + 3^{n-k} = 2^{n+1}-1\] The two equations are essentially the same as you can replace $k$ by $n-k$ in one to get the other.

This is a number theory problem so its likely we need to use divisibilities and on the LHS there's a power of 3 divisor which then would have to divide $2^{n+1}-1$. What is this power of 3? It's the smaller of the two powers. Let's say $k\leq n-k$ so we have one of the two equations: \[3^k(1+2\cdot 3^{n-2k})=2^{n+1}-1\] \[3^k(2+3^{n-2k})=2^{n+1}-1\] What now? It certainly seems that we're not anywhere closer, as we have $3^k\mid 2^{n+1}-1$ which certainly can happen.

Here's one instance where having taking algebra can be helpful. I saw online that the official solution doesn't use any algebra, but I did and I think it's instructive. How would algebra reformulate the divisibility $3^k\mid 2^{n+1}-1$? It would say that $2^{n+1}=1$ in the finite group $(\mathbb{Z}/3^k \mathbb{Z})^\times$. One of the standard facts from algebra (eg I did this in honors algebra 3 when I taught this last year) is that the group $(\mathbb{Z}/3^k \mathbb{Z})^\times$ is cyclic but, while helpful to not be scared of this finite group, this isn't necessary. An even more basic fact from algebra is that if $2^{n+1}=1$ in the group then the order of the element 2 must divide the exponent $n+1$.

So my next step had to be computing the order $m$ of 2 in this finite group. Well, I essentially knew the answer (again from experience). The order of any element has to divide the cardinality of the finite group, in this case $\varphi(3^k)=2\cdot 3^{k-1}$ so $m$ is either a power of 3 or twice a power of 3. Then playing around (riffing on exercise 2 from induction from lecture 3) I showed by induction that \[2^{3^r}\equiv -1+3^{r+1}\pmod{3^{r+2}}\] \[2^{2\cdot 3^r}\equiv 1+3^{r+1}\pmod{3^{r+2}}\] If the order $m$ was a power of 3 then $2^m-1$ is not even divisible by 3, let alone $3^k$ (though I had to keep in mind the case $k=0$ for the end). So $m=2\cdot 3^r$ and looking at the above formula if $3^k\mid 2^m-1$ then the smallest value of $m$ was exactly $\varphi(3^k)=2\cdot 3^{k-1}$.

With this in hand I could write $n+1 = 2\cdot 3^{k-1} t$ for some positive integer $t$ and now my life simplified enormously because the two equations (in their original form) $3^k + 2\cdot 3^{n-k}=2^{n+1}-1$ and $2\cdot 3^k + 3^{n-k}=2^{n+1}-1$ involve essentially a $3^n$ on one side and a $2^n$ on the other side where $n$ is exponentially larger than $k$. But then $3^n$ is super exponentially larger than $2^n$ so I could eliminate most values quickly.

To do the actual computations I noted that the LHS of both equations are $\geq 3^{n-k}$ and the RHS is $\leq 2^{n+1}$. So in either case I'd need $3^{n-k}\leq 2^{n+1}$ which I rewrote as $(3/2)^{n+1} \leq 3^{k+1}$. Plugging in $n+1=2\cdot 3^{k-1}t$ I got \[1.5^{2\cdot 3^{k-1}\cdot t}\leq 3^{k+1}\] Now $1.5^3\gt 3$ (same reason that $\sqrt[3]{3}\gt\sqrt{2}$ so the LHS is \[1.5^{2t\cdot 3^{k-1}}\geq 2.25^t \cdot 3^{3^{k-2}}\geq 3^{3^{k-2}}\] so I'd certainly need that $3^{k-2}\leq k+1$ (setting asside $k=1$ for the end). But $3^{k-2}\leq k+1$ happens only when $k\leq 3$ (just play around a little).

We're left with the special cases $k=0,1,2,3$. I don't actually remember how I finished this off, but most likely I brute-force checked each of these possibilities, since it worked so well until now.

Say you try $k=3$ (the others are even easier). Then $n+1 = 18t$ and so you've solving \[3^3 + 2\cdot 3^{18t-4}\textrm{ or }2\cdot 3^3+3^{18t-4} = 2^{18t}-1\] I'd need that $3^{6t}\lt 1.5^{18t}\lt 3^4$ so get a contradiction because $6t\geq 4$.

Let's do $k=2$, in which case $n+1=6t$ so you're solving \[3^2+2\cdot 3^{6t-3}\textrm{ or }2\cdot 3^2+3^{6t-3}=2^{6t}-1\] Again you need $3^{2t}\lt 1.5^{6t}\lt 3^3$ so $t$ would have to be 1 and so $n=5$. Solving the quadratic in $m$ yields $m=9,54$.

Let's do $k=1$, in which case $n+1=2t$. We need to solve \[3+2\cdot 3^{2t-2}\textrm{ or }6+3^{2t-2} = 4^t-1\] You'd need $(9/4)^t\lt 9$ so $t=1,2$ which gives $n=1,3$. Solving the quadratics you'd get $m=6,9$ when $n=3$ and no solutions when $n=1$.

Finally, when $k=0$ we need to solve \[1+2\cdot 3^n\textrm{ or }2+3^n = 2^{n+1}-1\] You'd need $1.5^n\lt 2$ so $n=1$ and again the quadratic in $m$ has no integer solutions.

Notes on VTRMC 2017

The problems

How I approached the problems