Math 20550 Calculus III In-class Exercises
A list of exercises and their solutions to work on during class.
Wednesday, May 2, 2016 (Review of some recent topics)
- Integrate functions
- Over (nonoriented) curves parametrized by $r(t)$ for $a\leq t\leq b$: \begin{align} \int_C fds&= \int_a^b f(r(t))|r'(t)|dt\\ \int_C fdx&= \int_a^b f(r(t))x'(t)dt \end{align}
- Over (nonoriented) surfaces parametrized by $r(u,v)$ for $(u,v)\in D$ a region in the plane \begin{align} \iint_S fdS&=\iint_D f(r(u,v))|r_u\times r_v|dudv \end{align}
- Integrate vector fields
- Over oriented curves $\displaystyle\int_C F\cdot dr$.
- Use the parametrization (being careful about the orientation of the curve given to you and the one implicit in the parametrization). Then $\displaystyle \int_C F\cdot dr= \int_a^b F(r(t))\cdot r'(t)dt$.
- If $F$ is conservative you may use the fundamental theorem of line integrals $\displaystyle \int_C \nabla f\cdot r =f(r(b))-f(r(a))$. Here $f$ is a function which takes scalar (not vector) values.
- If $C$ is closed you may use Green's theorem or Stokes' theorem.
- Over oriented surfaces $\iint_S F\cdot dS$.
- Use the parametrization (being careful about the orientation of the surface given to you and the one implicit in the parametrization). \[\iint_S F\cdot dS = \iint_D F(r(u,v))\cdot(r_u\times r_v)dudv\]
- If $F=\operatorname{curl}G$ you may use Stokes' theorem.
- If $S$ is closed you may use the div theorem.
- Over oriented curves $\displaystyle\int_C F\cdot dr$.
Exercise 1: Consider the surface $S$ which lies inside the cylinder $x^2+y^2=1$ and on the graph of the function $z=(x^2+y^2)^{5/2}$.
- Parametrize the surface. Answer: either $f(x,y)=\langle x,y,(x^2+y^2)^{5/2}\rangle$ for $(x,y)\in D$ the unit disc, or $f(r,\theta)=\langle r\cos\theta, r\sin\theta, r^5\rangle$ for $0\leq \theta\leq 2\pi$ and $0\leq r\leq 1$.
- Write an integral that computes the area. Answer: either $\displaystyle \iint_S 1dS=\iint_D \sqrt{1+25(x^2+y^2)^4}dxdy$ in the first parametrization or $\int_0^{2\pi}\int_0^1 \sqrt{25r^{10}+r^2}drd\theta$. After a change to polar coordinates the former integral is the same as the latter.
Exercise 2: Compute the tangent plane to the surface parametrized by $r(u,v)=\langle 4-u^2-v^2,2u,v\rangle$ at the point $(2,2,1)$. Answer: $2(x-2)+2(y-2)+4(z-1)=0$.
Exercise 3: Evaluate $\displaystyle \int_C x^2dx+y^2dy+z^2dz$ where $C$ is parametrized by $r(t)=\langle t,t^2,t^3\rangle$ for $0\leq t\leq 1$. Answer: 1.
Exercise 4: Let $C$ be a simple closed curve that lies in the $xy$-plane. The curve $C$ is oriented clockwise when viewed from above and it encloses a region of area 2. Use Stokes' Theorem to compute $\displaystyle \int_C\langle z/2, x/3, y/4\rangle\cdot dr$. Answer: $-2/3$.
Exercise 5: Let $S$ be the surface of the solid bounded by $y+z=2$, $x=3$ and the three coordinate planes $x=0$, $y=0$ and $z=0$. Compute the flux of $F=\langle 2ye^z, z^2-y, 3\cos(x)\rangle$ across $S$ oriented inwards. Answer: 6.
Exercise 6: Find the flux of the electric field $E(x,y,z)=\langle x/(x^2+y^2), y/(x^2+y^2), 1\rangle$ over a surface with downwards orientation whose parametric equation is given by $r(u,v)=\langle u,v, 1-u^2-v^2\rangle$ for $(u,v)$ such that $u^2+v^2\leq 1$. [Caveat: the orientation matters.] Answer: $-3\pi$.
Wednesday, April 25, 2018 (Stokes' theorem)
Exercise 1: Use Stokes' theorem to evaluate \[\iint_S\operatorname{curl}\langle e^{xy}, e^{xz}, x^2z\rangle\cdot dS\] where $S$ is the half of the ellipsoid $4x^2+y^2+4z^2=4$ that lies to the right of the $xz$-plane, oriented in the positive $y$-direction.
Solution: Applying Stokes get
\[\iint_S\operatorname{curl}\langle e^{xy}, e^{xz},
x^2z\rangle\cdot dS=\int_C \langle e^{xy}, e^{xz},
x^2z\rangle\cdot dr\]
What is $C$? The boundary of the ellipsoid lies in the
$xz$-plane and so the equation of $C$ is $4x^2+4z^2=4$, i.e.,
$x^2+z^2=1$. So $C$ is a circle of radius 1. As $S$ is
oriented in the positive $y$-direction, $C$ is oriented
counterclockwise when seen from the positive $y$
direction.
We parametrize $C$ as $r(t)=\langle \cos t, 0,\sin t\rangle$
which gives exactly the same orientation with $r'(t)=\langle
-\sin t, 0, \cos t\rangle$. So
\begin{align}
\int_C \langle e^{xy}, e^{xz},
x^2z\rangle\cdot dr&=\int_0^{2\pi}\int_C \langle 1, e^{\cos
t\sin t},
\cos^2 t\sin t\rangle\cdot \langle -\sin t, 0, \cos t\rangle
dt\\
&=\int_0^{2\pi}\sin t(\cos^3 t-1)dt\\
&=0
\end{align}
Exam 3 Review, April 23, 2018
Remarks:
- If in a change of variables $u$ and $v$ are given as functions of $x$ and $y$ but you need the Jacobian $\dfrac{\partial (x,y)}{\partial(u,v)}$ you don't actually need to find $x$ and $y$ in terms of $u$ and $v$ to plug into the definition of the Jacobian. Instead, you can use \[\dfrac{\partial (x,y)}{\partial(u,v)}= \frac{1}{\dfrac{\partial(u,v)}{\partial (x,y)}}\] which saves you a little time.
- You can only apply Green's theorem for curves which are closed. Don't ever try it for curves which are not closed.
Integrals and changes of variables:
- Find the center of mass of the disc bounded by the circle $x^2+y^2= 4$ with density $\rho(x,y)=x^2+y^2$. (Answer: $(0,0)$.)
- Compute the volume enclosed by the paraboloid $z=x^2+y^2$ and the plane $z=1$. (Answer: $\pi/2$.)
- Let $S$ be the solid inside both the cone $z=\sqrt{x^2+y^2}$ and the sphere $x^2+y^2+z^2=9$. Write $\displaystyle\iiint_S z\ dV$ in spherical coordinates. (Answer: $\displaystyle \int_0^{2\pi}\int_{0}^{\pi/4}\int_0^3 \rho^3\cos\phi\sin\phi d\rho d\phi d\theta$.)
- Compute the Jacobian $\dfrac{\partial(x,y)}{\partial(u,v)}$ of the transformation $x=e^{u-v}$ and $y=e^{u+v}$. (Answer: $2e^{2u}$.)
- Evaluate the triple integral $\displaystyle \iiint_E x dV$ where $E$ lies under the plane $z=1$ and above the region in the $xy$-plane bounded by $x=0$, $y=0$ and $2x+y=2$. (Answer: $1/3$.)
- Use the transformation $u=x-2y$, $v=3x-y$ to evaluate $\displaystyle \iint_R\frac{\sin(x-2y)}{3x-y}dA$ where $R$ is the parallelogram enclosed by the lines $x-2y=0$, $x-2y=4$, $3x-y=1$, and $3x-y=8$. (Answer: $\ln(8)/5$.)
- Rewrite $\displaystyle \int_0^3\int_0^{2-\frac{2z}{3}}\int_0^{6-2z-3y}\frac{e^z}{(z+2)(6-z)}dxdydz$ as an integral of $dydxdz$. (Answer: $\displaystyle \int_0^3\int_0^{6-2z}\int_0^{(6-2z-x)/3}\frac{e^z}{(z+2)(6-z)}dxdydz$.)
Line integrals:
- A thin wire in space has the shape of the helix $C$ given by $r(t)=\langle \cos(3t), \sin(3t), 3\sqrt{3}t\rangle$ for $0\leq t\leq 2\pi$ and has density $\rho(x,y,z)=\dfrac{z}{x^2+y^2}$. Compute the mass of $C$. (Answer: $36\sqrt{3}\pi^2$.)
- Compute $\int_CF\cdot dr$ where $F=\langle -2xy,4y,1\rangle$ and $C$ is given by $r(t)=\langle t,t^2,1\rangle$ for $0\leq t \leq 2$. (Answer: $24$.)
- Find a function $f(x,y)$ such that $\nabla f=\langle 2xe^{x^2y}+2x^3ye^{x^2y}+2xe^{x^2}, x^4e^{x^2y}+2y\rangle$. (Answer: $x^2e^{x^2y}+e^{x^2}+y^2$.)
- Let $F=\nabla f$ where $f(x,y)=x^2\cos(y)+e^{\sin(y)}$. Evaluate $\int_CF\cdot dr$ where $C$ is the semicircle $x^2+y^2=1$, $x\geq 0$ and the orientation is counterclockwise. (Answer: $e^{\sin(1)}-e^{\sin(-1)}$.)
Green's theorem, div and curl:
- Use Green's theorem to rewrite $\displaystyle \int_C (y^2+(\sin x) e^x-2x)dx + (x^2+(y\cos y)e^{y^2}+2-3x)dy$ as a double integral over the unit disc, where $C$ is the boundary of the unit disc with clockwise orientation. (Answer: $\displaystyle \iint_D (2x-3+2y)dA$.)
- Compute curl of the vector field $\langle 2x+y^2, 3y+z^3, 4z+x^4\rangle$. (Answer: $\textrm{curl}F = \langle -3z^2,-4x^3,-2y\rangle$.)
- Is the vector field from the previous exercise incompressible? (Answer: $\textrm{div}F = 9\neq 0$ so no.)
Parametric surfaces and surface integrals:
- Find an equation of the tangent plane to the given parametric surface $r(u,v)=\langle u^2, 2u\sin v, 2u\cos v\rangle$ at the point $u=1, v=0$. (Answer: $-x+2z=1$.)
- Find parametric equations for the surface obtained by rotating the curve $x=1/y$$, y\geq 1$, about the $y$-axis. (Answer: $\langle \cos\theta/y, y, \sin\theta/y\rangle$.)
- Compute the area of the surface $r(u,v)=\langle u^2,uv,v^2/2\rangle$ for $0\leq u\leq 1$, $0\leq v\leq 2$.(Answer: $4$.)
Friday, April 20, 2018 (Surface and flux integrals)
Exercise 1: Let $S$ be the portion of the sphere of radius 1 parametrized in spherical coordinates by $\frac{\pi}{6}\leq \phi,\theta\leq\frac{\pi}{3}$. Give $S$ the outwards orientation. Compute the flux of $F=\langle 0, 1/y, 1/x\rangle$.
Solution: First, we parametrize $S$ using
\[f(\phi,\theta)=\langle\sin\phi\cos\theta,\sin\phi\sin\theta,\cos\phi\rangle\]
and compute the normal vector
\[f_\phi\times f_\theta =
\langle\sin^2\phi\cos\theta,\sin^2\phi\sin\theta,\sin\phi\cos\phi\rangle\]
(check this!) and see that this is oriented outwards as well,
which means that this parametrization induces the desired
orientation on $S$ so we can compute the flux.
Then we compute (the region $D$ is given by
$\{(\phi,\theta)\mid \frac{\pi}{6}\leq \phi,\theta\leq\frac{\pi}{3}\}$)
\begin{align}
\iint_SF\cdot dS &=\iint_D F(f(\phi,\theta))\cdot
(f_\phi\times f_\theta)d\phi d\theta\\
&=\iint_D \langle 0,
\frac{1}{\sin\phi\sin\theta},\frac{1}{\sin\phi\cos\theta}\rangle
\cdot
\langle\sin^2\phi\cos\theta,\sin^2\phi\sin\theta,\sin\phi\cos\phi\rangle d\phi d\theta\\
&=\int_{\pi/6}^{\pi/3}\int_{\pi/6}^{\pi/3} (\sin\phi+\frac{\cos\phi}{\cos\theta})d\phi d\theta\\
&=\int_{\pi/6}^{\pi/3}\frac{\sqrt{3}-1}{2}(1+\sec(\theta))d\phi d\theta\\
&=\frac{\sqrt{3}-1}{2}(\theta+\ln|\sec\theta+\tan\theta|)|_{\pi/6}^{\pi/3}\\
&=\frac{\sqrt{3}-1}{2}\left(\frac{\pi}{6}+\ln\left(\frac{2+\sqrt{3}}{\sqrt{3}}\right)\right)
\end{align}
Exercise 2: The surface $S$ is the part of the paraboloid $z=x^2+y^2$ when $1\leq z\leq 4$.
- Parametrize $S$.
- Compute $\displaystyle \iint_S(1+4z)dS$.
Solution: Using cylindrical coordinates
$x=r\cos \theta$, $y=r\sin\theta$, $z=x^2+y^2=r^2$ for $0\leq
\theta\leq 2\pi$ and $1\leq z=r^2\leq 4$ so $1\leq r\leq
2$.
With the parametrization $f(r,\theta)=\langle
r\cos\theta,r\sin\theta, r^2\rangle$ the normal vector is
\[f_r\times f_\theta=\langle -2r^2\cos(\theta),
-2r^2\sin(\theta), r\rangle\]
with length $|f_r\times f_\theta|=\sqrt{4r^4+r^2}$.
Then
\begin{align}
\iint_S (1+4z)dS&=\int_0^{2\pi}\int_1^2 (1+4r^2)
\sqrt{4r^4+r^2}drd\theta\\
&=\int_0^{2\pi}\int_1^2 r (1+4r^2)^{3/2}drd\theta\\
&=\int_0^{2\pi}\int_{5}^{17}\frac{1}{8}u^{3/2}dud\theta\\
&=\int_0^{2\pi}\frac{1}{20}u^{5/2}|_5^{17}dud\theta\\
&=2\pi \frac{17^{5/2}-5^{5/2}}{20}
\end{align}
with the change of variables $u = 1+4r^2$ with $du=8dr$.
Using the graph parametrization we could
choose $f(x,y)=\langle x, y, x^2+y^2\rangle$ for $x^2+y^2$
between 1 and 4, i.e., $(x,y)\in D$ the annulus with radii 1
and 2. Then $|f_x\times
f_y|=\sqrt{1+z_x^2+z_y^2}=\sqrt{1+4(x^2+y^2)}$.
Then
\begin{align}
\iint_S(1+4z)dS&=\iint_D (1+4(x^2+y^2))
\sqrt{1+4(x^2+y^2)}dxdy
\end{align}
which after a change to polar coordinates is
\[\int_0^{2\pi}\int_1^2 (1+4r^2)\sqrt{1+4r^2} rdrd\theta\]
which is the same integral as above. The $r$ from
$rdrd\theta$ in the previous method initially appeared inside
the square root.
Wednesday, April 16, 2018 (Parametric surfaces)
Exercise 1: Express as an integral in polar coordinates the area of the surface $z=\cos(x^2+y^2)$ inside the cylinder $x^2+y^2=1$. Do NOT compute this integral.
Solution: There's two ways to do
this. First, we can parametrize as $f(x,y)=\langle
x,y,z(x,y)\rangle$ with respect to which we know from class that
$|f_x\times
f_y|=\sqrt{1+z_x^2+z_y^2}=\sqrt{1+4(x^2+y^2)\sin^2(x^2+y^2)}$
and so
\begin{align}
\operatorname{area} &=\iint_{x^2+y^2\leq 1}
\sqrt{1+4(x^2+y^2)\sin^2(x^2+y^2)}\\
&=\int_0^{2\pi}\int_0^1 \sqrt{1+4r^2\sin^2(r^2)}rdrd\theta
\end{align}
after a change into polar coordinates.
Another way is to directly parametrize in polar coordinates as
\[f(r,\theta)=\langle r\cos\theta,r\sin\theta,\cos(r^2)\rangle\]
Then $f_r = \langle\cos\theta,\sin\theta,-2r\sin(r^2)\rangle$
and $f_\theta=\langle -r\sin\theta,r\cos\theta,0\rangle$ and so
\[f_r\times f_\theta = \langle 2r^2\sin(r^2)\cos\theta,
2r^2\sin(r^2)\sin(\theta), r\rangle\]
which has length $|f_r\times
f_\theta|=\sqrt{r^2+4r^4\sin^2(r^2)}$ yielding
\[\operatorname{area}=\int_0^{2\pi}\int_0^1
\sqrt{r^2+4r^4\sin^2(r^2)}drd\theta\]
which is the same formula as above, with the difference that
the $r$ was put into the square root.
Exercise 2: The Mobius strip is the surface parametrized by $x=2\cos(\theta)+r\cos(\theta/2)$, $y=2\sin(\theta)+r\cos(\theta/2)$ and $z=r\sin(\theta/2)$ where $-1/2\leq r\leq 1/2$ and $0\leq\theta\leq 2\pi$. Find an equation for the tangent plane to this surface at the point $(1,\sqrt{3},0)$.
Solution: First we find $r$ and $\theta$
such that $f(r,\theta)=(1,\sqrt{3},0)$. The values are $r=0$ and
$\theta=\pi/3$.
Next, we compute \[f_r=\langle \cos(\theta/2), \cos(\theta/2),
\sin(\theta/2)\rangle\] which gives $f_r(0,\pi/3)=\langle
\sqrt{3}/2,\sqrt{3}/2,1/2\rangle$. Then \[f_\theta=\langle
-2\sin(\theta)-(r/2)\sin(\theta/2),
2\cos(\theta)-(r/2)\sin(\theta/2), r\cos(\theta)\rangle\] which gives
$f_\theta(0,\pi/3)=\langle -\sqrt{3}, 1, 0\rangle$.
Their product is $f_r\times f_\theta=\langle
-\frac{1}{2},\,-\frac{1}{2} \, \sqrt{3},\,\frac{1}{2} \,
\sqrt{3} + \frac{3}{2}\rangle$. The equation of the tangent
plane is therefore
\[-1/2(x-1)-\sqrt{3}/2(y-\sqrt{3})+(\sqrt{3}+3)/2 z = 0\]
Friday, April 13, 2018 (Div and curl)
Exercise 1: Find a value of $p$ for which the vector field $F(x,y,z)=\dfrac{\vec{r}}{r^p}$ is incompressible. Here $\vec{r}=\langle x,y,z\rangle$ and $r=|\vec{r}|$.
Solution: We write $F=\langle x/r^p,y/r^p,z/r^p\rangle$ with div \[\operatorname{div}(f)=\partial_x (x/r^p)+\partial_y(y/r^p)+\partial_z(z/r^p)\] Use the quotient rule to get \[\partial_x \frac{x}{r^p}=\frac{r^p - x\partial_x(r^p)}{r^{2p}}\] Now use the chain rule to compute \[\partial_x r^p = pr^{p-1}\partial_xr\] where \[\partial_xr = \partial_x \sqrt{x^2+y^2+z2}=\frac{2x}{2\sqrt{x^2+y^2+z^2}}=\frac{x}{r}\] Putting everything together we get $\partial_x(r^p) = px^2r^{p-2}$ and therefore \[\partial_x(x/r^p)=\frac{r^p-px^2r^{p-2}}{r^{2p}}\] Now we compute \begin{align}\operatorname{div}(f)&=\partial_x (x/r^p)+\partial_y(y/r^p)+\partial_z(z/r^p)\\ &=\frac{r^p-px^2r^{p-2}}{r^{2p}}+\frac{r^p-py^2r^{p-2}}{r^{2p}}+\frac{r^p-pz^2r^{p-2}}{r^{2p}}\\ &=\frac{3r^p-p(x^2+y^2+z^2)r^{p-2}}{r^{2p}}\\ &=\frac{3r^p-pr^{p}}{r^{2p}}\\ &=\frac{3-p}{r^p} \end{align} Therefore the vector field is incompressible exactly when $p=3$. We used that $x^2+y^2+z^2=r^2$.
Exercise 2: Determine if there exists a vector field $F$ such that \[\operatorname{curl}F=\langle x\sin y,\cos y,z-xy\rangle\]
Solution: We compute \[\operatorname{div}\langle x\sin y,\cos y,z-xy\rangle=\sin(y)-\sin(y)+1=1\] which is not 0. Therefore not such vector field exists.
Wednesday, April 11, 2018 (Green's theorem)
Exercise 1: Consider the vector field $F(x,y)=\langle xy+\cos x,2x^2+\tan y\rangle$. The curve $C$ consists of the circle of radius $1/2$ centered at $(1/2,0)$ going clockwise together with the circle of radius $1$ centered at $(1,0)$ going counterclockwise.
- Sketch the oriented curve $C$.
- Describe the region inside $C$ in polar coordinates.
- Compute $\displaystyle \int_CF\cdot d\vec{r}$.
Solution:
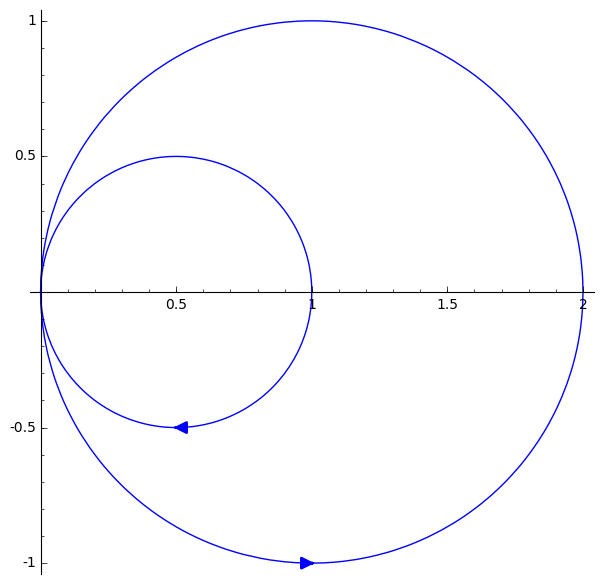
- In polar coordinates the region $D$ whose boundary is the positively oriented curve $C$ is given by $-\dfrac{\pi}{2}\leq\theta\leq\dfrac{\pi}{2}$ and $\cos\theta\leq r\leq 2\cos\theta$.
- We use Green's theorem to compute \begin{align}\int_CF\cdot d\vec{r}&=\iint_D (Q_x-P_y)dA\\ &=\iint_D 3x dA\\ &=\int_{-\pi/2}^{\pi/2}\int_{\cos\theta}^{2\cos\theta}3r^2\cos\theta drd\theta\\ &=\int_{-\pi/2}^{\pi/2}7\cos^4\theta d\theta \end{align} Now we use double angle formulae $\cos^2x = \frac{1+\cos(2x)}{2}$ to compute \begin{align} 7\int_{-\pi/2}^{\pi/2}\cos^4\theta d\theta&=7\int_{-\pi/2}^{\pi/2}(\frac{1+\cos(2\theta)}{2})^2 d\theta\\ &=7\int_{-\pi/2}^{\pi/2}\frac{1+2\cos(2\theta)+\cos^2(2\theta)}{4} d\theta\\ &=7\int_{-\pi/2}^{\pi/2}\frac{1+2\cos(2\theta)+\frac{1+\cos(4\theta)}{2}}{4} d\theta\\ &=7\int_{-\pi/2}^{\pi/2}\frac{3+4\cos(2\theta)+\cos(4\theta)}{8} d\theta\\ &=\frac{21\pi}{8} \end{align}
Monday, April 9, 2018 (Conservative vector fields)
Exercise 1: Determine if the vector field \[F(x,y)=\langle \cos(x)\ln(y),\dfrac{\sin(x)}{y}\rangle\] is conservative.
Solution: Indeed \[P_y = \frac{\cos(x)}{y}=Q_x\] so the vector field is conservative.
Exercise 2: Compute the work of the vector field $F(x,y)=\langle \dfrac{1}{2\sqrt{xy}}, -\dfrac{1}{2}\sqrt{\dfrac{x}{y^3}}\rangle$ along the semicircle with endpoints $(1,1)$ and $(4,9)$. [Hint: Is the vector field conservative?]
Solution: It's worth checking that the
vector field is indeed conservative.
\[P_y = -\frac{1}{4\sqrt{xy^3}}=Q_x\]
Next, we seek $f(x,y)$ such that $\nabla f=F$. In other words
we want
\[\begin{cases}f_x=\dfrac{1}{2\sqrt{xy}}\\f_y=-\dfrac{1}{2}\sqrt{\dfrac{x}{y^3}}\end{cases}\]
Integrating the first equation we get
\[f = \int \dfrac{1}{2\sqrt{xy}}dx =
\sqrt{\dfrac{x}{y}}+DND_x\]for a constant $DND_x$ which does
not depend on $x$. Similarly integrating the second equation
we get
\[f = \int -\dfrac{1}{2}\sqrt{\frac{x}{y^3}}dy =
\sqrt{\dfrac{x}{y}}+DND_y\]for a constant $DND_y$ which does
not depend on $y$.
We conclude that $F(x,y)=\nabla\sqrt{\dfrac{x}{y}}$ so
\[\int_CF\cdot dr = \sqrt{\dfrac{x}{y}}\mid_{(1,1)}^{(4,6)}=\sqrt{\dfrac{4}{6}}-\sqrt{\dfrac{1}{1}}=-\dfrac{1}{3}\]
Friday, April 6, 2018 (Vector field integrals)
Exercise 1: The curve $C$ is parametrized by $\vec{r}(t)=\langle 1-\sin t, t-\cos t\rangle$.
- Set up the integral that computes the work done by the force field $\vec{F}(x,y)=\langle x,y\rangle$ along the curve between $t=0$ and $t=\pi$.
- Compute this integral.
Solution: For the first part: $\vec{r}(t) = \langle 1-\sin t, t-\cos t\rangle$ and $\vec{r}'(t) = \langle -\cos t, 1+\sin t\rangle$ so \begin{align}\int_C\vec{F}\cdot d\vec{r} &= \int_0^\pi \vec{F}(\vec{r}(t))\cdot \vec{r}'(t)dt\\ &=\int_0^\pi \langle 1-\sin t, t-\cos t\rangle\cdot \langle -\cos t, 1+\sin t\rangle dt\\ &=\int_0^\pi (t+t\sin(t)-2\cos(t))dt\\ \end{align} For the second part we further compute \[\int_0^\pi t\sin(t)dt = \int_0^\pi t d(-\cos(t)) = -t\cos(t)|_0^\pi +\int_0^\pi\cos tdt=\pi\] so the final answer is \[\int_C\vec{F}\cdot d\vec{r}=\pi^2/2 +\pi\]
Exercise 2: Suppose $F$ is the vector field $F(x,y)=\langle x,-y\rangle$.
- Sketch the vector field.
- If at $t=0$ a particle is at $(2,3)$ where will the particle be at time $t=1$ if you approximate the motion in time increments of $0.5$.
Solution:

Write $r(t)$ for the approximate position at time
$t$. Then $r(0.5)= r(0)+0.5\cdot v(0)$ and
$v(0)=F(r(0))=F(2,3)=\langle 2,-3\rangle$. So $r(0.5) =
\langle 2,3\rangle +0.5\langle 2,-3\rangle = \langle 3,
1.5\rangle$.
Next $r(1)=r(0.5)+0.5\cdot v(0.5)$ and
$v(0.5)=F(r(0.5))=\langle 3,-1/5\rangle$. We get
$r(1)=\langle 4,0.75\rangle$.
Wednesday, April 4, 2018 (Line integrals)
Exercise 1: The cylinder $x^2+y^2=1$ intersects the plane $z=y$ in the region $z\geq 0$ in the curve $C$. Parametrize $C$. [Hint: Glance at your notes from the lecture on parametrizations. Caveat: the $\vec{r}$ in parametrizations is a vector, it has nothing to do with the radius $r$ in polar and cylindrical coordinates.]
Solution: This is similar to the example
from January 27.
The cylinder is parametrized by
$\langle \cos t,\sin t, z\rangle$ so its intersection with the
plane is
\[\vec{r}(t)=\langle \cos t, \sin t, \sin t\rangle\]
as on the plane the $y$ and $z$ coordinates are the same. The
condition that $z\geq 0$ is equivalent to $\sin(t)\geq 0$ so
$0\leq t\leq \pi$.
Exercise 2: The curve $C$ is the one from Exercise 1. Do one of the following two questions:
- Compute the mass of the half of $C$ contained in the first octant assuming density $\rho(x,y,z)=xy$.
- Set up the integrals that compute the center of mass of $C$ assuming constant density $\rho(x,y,z)=1$. [Remark: You cannot compute the integrals, so don't try.]
Solution:
First, we compute $r'(t)=\langle -\sin t,\cos t,\cos(t)\rangle$
so $|r'(t)|=\sqrt{1+\cos^2 t}$.
For the first part we only care about the first octant
which also means that $x\geq 0$ so $\cos(t)\geq 0$ so $0\leq
t\leq \pi/2$. We compute the mass
\begin{align}
m&=\int_C\rho ds\\
&=\int_0^{\pi/2}\cos(t)\sin(t)\sqrt{1+\cos^2 t}dt\\
&=\int_1^2\sqrt{u}du = \frac{2\sqrt{2}-1}{3}
\end{align}
having used the change of variables $u=1+\cos^2 t$ with
$du=-2\sin t \cos t dt$.
For the second part again $ds = |r'(t)|dt = \sqrt{1+\cos^2 t}dt$ so
\begin{align}
m&=\int_C ds=\int_0^\pi\sqrt{1+\cos^2 t}dt\\
\overline{x}&=\frac{1}{m}\int_0^\pi \cos t\sqrt{1+\cos^2 t}dt\\
\overline{y}&=\frac{1}{m}\int_0^\pi \sin t\sqrt{1+\cos^2 t}dt\\
\overline{z}&=\overline{y}
\end{align}
Wednesday, March 28, 2018 (Change of variables in double integrals)
Exercise 1: Let $S$ be the parallelogram bounded by the lines $y=x$, $y=2x-2$, $y=x-2$ and $y=2x-4$. Let $u=2x-y$ and $v=x-y$. What is the image $R$ of the region $S$ under the change of variables $(x,y)\mapsto (u,v)$? Also compute $\dfrac{\partial(u,v)}{(x,y)}$.
Solution:
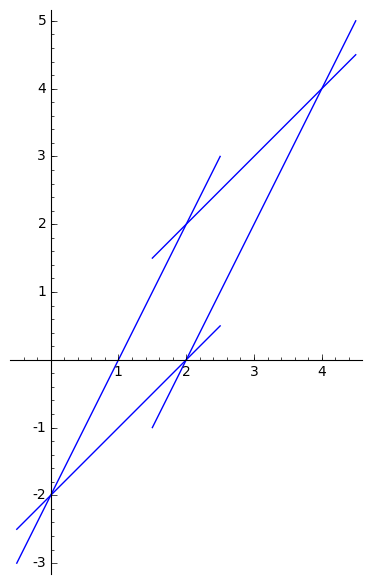
The line $y=x$ becomes the line $v=0$, the line $y=x-2$
becomes the line $v=2$, the line $y=2x-2$ becomes the line $u=2$
and the line $y=2x-4$ becomes the line $u=4$.
So the region $R$ is the square $\{(u,v)\mid 2\leq u\leq 4,
0\leq v\leq 2\}$.
Exercise 2: Suppose $x=u/v$ and $y=v^2$. As the points $(u,v)$ vary in a region $S$ in the first quadrant, the points $(x,y)$ vary in the region $R$ bounded by the lines $y=x$ and $y=x/2$ and the curves $x^2y=1$ and $x^2y=4$. Describe the region $S$? Also compute $\dfrac{\partial(x,y)}{(u,v)}$.
Solution:
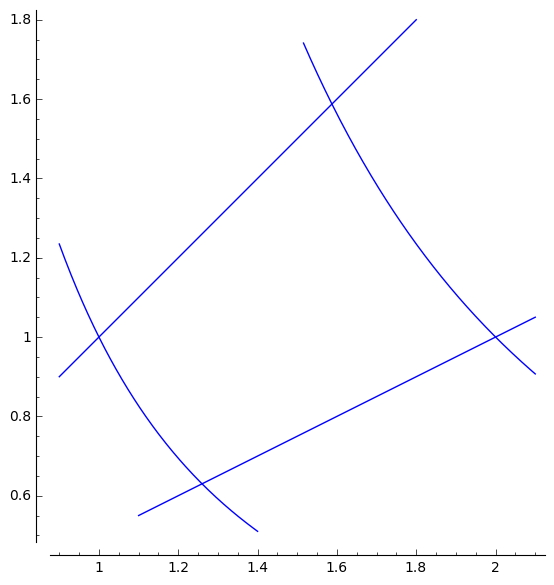
The curve $x^2y=1$ becomes $(u/v)^2v^2=1$ so $u^2=1$ and
similarly $x^2y=4$ becomes $u^2=4$. As $u\geq 0$ being in the
first quadrant these equations become $u=1$ and $u=2$.
The equations $y=x$ (and $y=x/2$) become $v^2 = u/v$ (and
$v^2=u/(2v)$) which can be rewritten as $u=v^3$ (and
$u=2v^3$).
So the region $S$ is contained between the lines $u=1$ and
$u=2$ and the curves $u=v^3$ and $u=2v^3$.
Monday, March 26, 2018 (Spherical coordinates)
Exercise 1: Describe in spherical coordinates the region contained inside the unit sphere centered at the origin and inside the cone with tip at the origin, having the $z$-axis as its axis, and $45^\circ$ angle between the axis and its sides.
Solution: The sphere is $0\leq \rho\leq 1$ and the cone is $0\leq \phi\leq \pi/4$ so the region is described by $0\leq \theta\leq 2\pi$, $0\leq \phi\leq \pi/4$ and $0\leq \rho\leq 1$.
Exercise 2: Compute the volume of this region.
Solution: The volume of the region $R$ is \begin{align}\iiint_R 1dV&=\int_0^{2\pi}\int_0^{\pi/4}\int_0^1 \rho^2\sin\phi d\rho d\phi d\theta\\ &=\frac{1}{3}\int_0^{2\pi}\int_0^{\pi/4} \sin\phi d\phi d\theta\\ &=\frac{1}{3}\int_0^{2\pi}(-\cos\phi)|_0^{\pi/4} d\theta\\ &=\frac{1}{3}\int_0^{2\pi}(1-\frac{1}{\sqrt{2}}) d\theta\\ &=\frac{2\pi}{3}(1-\frac{1}{\sqrt{2}}) \end{align}
Friday, March 23, 2018 (Cylindrical coordinates)
Exercise 1: Describe in cylindrical coordinates the region contained inside the unit sphere centered at the origin and inside the cone with tip at the origin, having the $z$-axis as its axis, and $45^\circ$ angle between the axis and its sides.
Solution: We describe each region
separately. Inside the sphere is $0\leq \theta\leq 2\pi$, $0\leq
r\leq 1$ and $-\sqrt{1-r^2}\leq z\leq \sqrt{1-r^2}$. Inside the
cone is $0\leq \theta\leq 2\pi$ and $r\leq z$.
When do the two surfaces intersect? It has to be that
$z=r$ from the cone and $z=\sqrt{1-r^2}$ from the sphere so
$r=\sqrt{1-r^2}$ which gives $r=1/\sqrt{2}$. Thus the farthest
one can be from the $z$-axis is $1/\sqrt{2}$.
The region is therefore $0\leq \theta\leq 2\pi$, $0\leq r\leq
1/\sqrt{2}$ and $r\leq z\leq \sqrt{1-r^2}$.
Exercise 2: For the region $R$ above rewrite the triple integral $\displaystyle \iiint_R f(x,y,z)dV$ in cylindrical coordinates.
Solution: \begin{align} \iiint_R f(x,y,z)dV&=\int_0^{2\pi}\int_0^{1/\sqrt{2}}\int_r^{\sqrt{1-r^2}}f(x,y,z)rdzdrd\theta \end{align}
Wednesday, March 21, 2018 (Triple integrals)
Exercise 1: Compute the triple integral \[\iiint_D \frac{dV}{z}\] where $D=\{(x,y,z)\mid 0\leq x\leq 1, 0\leq y\leq 1, 1\leq z\leq e^{x+y}\}$.
Solution: \begin{align*} \iiint_D \frac{dV}{z}&=\int_0^1\int_0^1\int_1^{e^{x+y}}\frac{dz}{z}dydx\\ &=\int_0^1\int_0^1(x+y)dydx\\ &=\int_0^1(x+1/2)dx \\ &=1 \end{align*}
Exam 2 Review, Monday, March 19, 2018
Derivatives:
- Consider the surface $x+y^2=z^3$.
- What is the equation of the normal line at the point $(2,1,1)$? (Answer: $\langle 2,1,1\rangle + t\langle 1,2,-3\rangle$.)
- At what point does this line intersect the plane $x+2y+3z=3$? (Answer: $(3,3,-2)$.)
- What is $\displaystyle \frac{\partial z}{\partial x}$? (Answer: $\dfrac{1}{3z^2}$.)
- You are given two surfaces described by the equations $g(x,y,z)=3x^2+3y^2+z^2=7$ and $h(x,y,z)=x^2+y^2-2z^2=0$.
- Find an equation for the tangent line at $(1,1,1)$ to the curve of intersection of the two surfaces. (Answer: $\langle 1,1,1\rangle+t\langle -1,1,0\rangle$.)
- Suppose $f(x,y,z)$ is such that $\nabla f(1,1,1)=(1,0,0)$. In which direction should one travel along the curve of intersection in order to increase $f$? (Answer: In the direction $\langle 28,-28,0\rangle$.)
- In which direction $\vec{u}$ is $D_{\vec{u}}f(\pi/4,2)$ largest/smallest where $f(x,y) = \sin(x)y$? (Answer: Largest in the direction $\nabla f = \sqrt{\dfrac{2}{5}}\langle \sqrt{2}, 1/\sqrt{2}\rangle$ and smallest in the opposite direction.)
- If $z=e^{x+y}(y+5)$ where $y=st$ and $x=e^{-ts}$ compute $\dfrac{\partial z}{\partial t}$ when $t=0$ and $s=1$. (Answer: $e$.)
- Find an equation for the tangent plane to the surface $x^2+y^3-xy=z^2+x$ at the point $(1,1,0)$. (Answer: $y=1$.)
Optimization:
- Find and classify (i.e., min/max/saddle) the critical points of $f(x,y)=-4y^2+x^2y-2x+8$. (Answer: $(2,1/2)$ saddle.)
- Find and classify the critical points of the function \[f(x,y)=(x-1)x^2-\cos(y^2)\] (Answer: Second derivative test is inconclusive at $(0,0)$, $(2/3,0)$ but the other critical points are $(0,\sqrt{\textrm{odd}\cdot \pi})$ local max, $(2/3, \sqrt{\textrm{even}\cdot \pi})$ local min, $(0,\sqrt{\textrm{even}\cdot \pi})$ and $(2/3,\sqrt{\textrm{odd}\cdot \pi})$ saddle.)
- The function $f(x,y)=x^2y^3$ attains a maximum over the region $D=\{(x,y)\mid x^2+y^3\leq 1\}$. Find this maximum. (The function does not attain a minumum.) (Answer: $1/4$.)
Lagrange Multipliers:
- Find the absolute min and max of the function $f(x,y)=3x^2+2y^3+2$ subject to the condition $x^2+y^2=1$. (Answer: min 0, max 5.)
- Find the maximum and minimum values of $f(x,y,z)=2x-z$ subject to $x^2+10y^2+z^2=5$. (Answer: max 5, min $-5$.)
- Find the absolute min and max of $f(x,y,z)=2x+y$ with respect to the constraints $g(x,y,z)=2x^2+z^2=4$ and $h(x,y,z)=2x+y+3z=6$. (Answer: min 0 max 12.)
Double integrals:
- Sketch the region of integration for the double integral \[\int_1^3\int_y^{y^2}f(x,y)dxdy\] (Answer: The region has vertices $(1,1)$, $(3,3)$ and $(9,3)$.)
- Find the volume of the solid bounded by $x=\sqrt{y}$ and $x=y^3$ lying between $z=0$ and under $z=xy$. (Answer: $5/48$.)
Friday, March 9, 2018 (Mass, moments)
Exercise 1: Compute the mass of the region $D=\{(x,y)\mid |x|+|y|\leq 1\}$ with density function \[\rho(x,y)=2+x^2y^3-y^2\sin x.\] [Hint: Sketch the region first.]
Solution: The region looks like a diamond
having the origin as its center. Its vertices are $(1,0)$,
$(0,1)$, $(-1,0)$ and $(0,-1)$. While this region is symmetric,
the function is not and therefore you cannot use symmetries
directly.
There are two ways of doing the computation. The
first uses direct computations and needs integration by parts
twice. The second uses symmetries.
First (direct) solution. We break up $D$ into two pieces separated by the $y$-axis. The
first region $D_1$ is $-1\leq x\leq 0$ and $-x-1\leq y\leq
x+1$ (the left piece) and the second region $D_2$ is $0\leq
x\leq 1$ and $x-1\leq y\leq 1-x$.
We now compute
\begin{align*}
\iint_{D_1}(2+x^2y^3-y^2\sin
x)dA&=\int_{-1}^0\int_{-x-1}^{x+1}(2+x^2y^3-y^2\sin x)dydx\\
&=\int_{-1}^0\left(2y+x^2y^4/4-y^3\sin(x)/3\right)\left|_{-(x+1)}^{x+1}\right.dx\\
&=\int_{-1}^0\left(4(x+1)-2(x+1)^3\sin(x)\right)dx\\
&=12\sin(1)-8
\end{align*}
where the last line comes from integration by parts.
Similarly
\begin{align*}
\iint_{D_2}(2+x^2y^3-y^2\sin
x)dA&=\int_{0}^1\int_{x-1}^{1-x}(2+x^2y^3-y^2\sin x)dydx\\
&=\int_0^1\left(2y+x^2y^4/4-y^3\sin(x)/3\right)\left|_{x-1}^{1-x}\right.dx\\
&=\int_0^1\left(4(1-x)-2(1-x)^3\sin(x)\right)dx\\
&=12-12\sin(1)
\end{align*}
and again the last line is using integration by parts.
Putting everything together we get
\[\iint_D(2-x^2y^3+y^2\sin x)dA = 12\sin(1)-8+12-12\sin(1)=4\]
Second solution, using symmetries. We begin by
rewriting
\[\iint_D(2+x^2y^3-y^2\sin x)dA = \iint_D 2dA + \iint_D
x^2y^3dA +\iint_D y^2\sin xdA\]
First,
\[\iint_D 2dA = 2\cdot \textrm{area}(D) = 2\cdot
\sqrt{2}^2=4\]
Next, $f(x,y)=x^2y^3$ is antisymmetric in $y$ meaning that
$f(x,-y)=-f(x,y)$. As $D$ is symmetric with respect to the $x$
axis this means that $\iint_D x^2y^3dA = 0$. (Just as in Calc
2.)
Finally, $g(x,y)=y^2\sin(x)$ is antisymmetrix in $x$
meaning that $g(-x,y)=-g(x,y)$. As $D$ is symmetric with
respect to the $y$ axis we get that $\iint_D y^2\sin xdA=0$.
Putting everything together get that
\[\iint_D(2-x^2y^3+y^2\sin(x))dA = 4\]
Wednesday, March 7, 2018 (Double integrals in polar coordinates)
Exercise 1: Compute the double integral \[\iint_D e^{x^2+y^2}\frac{y}{\sqrt{x^2+y^2}}dA\] where $D=\{(x,y)\mid x^2+y^2\leq 1, y\geq 0\}$.
Solution: The region $D$ in polar coordinates is $0\leq \theta\leq 2\pi$ and $0\leq r\leq 1$. \begin{align*} \iint_De^{x^2+y^2}\frac{y}{\sqrt{x^2+y^2}}dA&=\int_0^\pi\int_0^1e^{r^2}\frac{r\sin\theta}{r}rdrd\theta\\ &=\int_0^\pi\int_0^1re^{r^2}\sin\theta drd\theta\\ &=\int_0^\pi \frac{1}{2}e^{r^2}\sin\theta|_0^1d\theta\\ &=\int_0^\pi (e-1)/2\sin\theta d\theta\\ &=e-1 \end{align*}
Exercise 2:
- Describe in polar coordinates (with inequalities) the region contained inside the cardiod $r=1+\cos(\theta)$ but outside the circle $r=3\cos(\theta)$.
- Compute the area of the region described above.
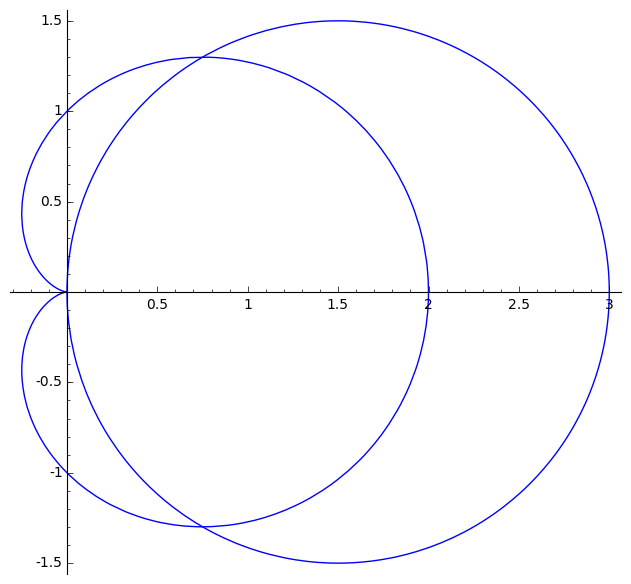 Let's describe the region in polar coordinates. The circle
imposes conditions only when $\theta$ is between $-\pi/2$ and
$\pi/2$ so the region inside the cardioid outside the circle
is described by
Let's describe the region in polar coordinates. The circle
imposes conditions only when $\theta$ is between $-\pi/2$ and
$\pi/2$ so the region inside the cardioid outside the circle
is described by
- $\pi/3\leq \theta\leq \pi/2$ and $3\cos\theta\leq r\leq 1+\cos\theta$
- $\pi/2\leq \theta\leq 3\pi/2$ and $0\leq r\leq 1+\cos\theta$ (in the left half-plane there is no circle)
- $3\pi/2\leq \theta\leq 3\pi/2+\pi/3$ and $3\cos\theta\leq r\leq 1+\cos\theta$
Part 2: We use the fact that the area of a region $D$ is $\iint_D 1dA$. We'll use a number of times that $\cos^2\theta=(1+\cos(2\theta))/2$.
Note that the region is symmetric with respect to the $x$-axis so it's enough to compute the area of the upper half. \begin{align} \frac{1}{2}\iint_D1dA&=\int_{\pi/3}^{\pi/2}\int_{3\cos\theta}^{1+\cos\theta}rdrd\theta + \int_{\pi/2}^{\pi}\int_0^{1+\cos\theta}rdrd\theta\\ &=\int_{\pi/3}^{\pi/2}r^2/2|_{3\cos\theta}^{1+\cos\theta}d\theta + \int_{\pi/2}^{\pi}r^2/2|_0^{1+\cos\theta}d\theta\\ &=\frac{1}{2}\int_{\pi/3}^{\pi/2}((1+\cos\theta)^2-9\cos^2\theta)d\theta + \frac{1}{2}\int_{\pi/2}^{\pi}(1+\cos\theta)^2d\theta\\ &=\frac{1}{2}\int_{\pi/3}^{\pi/2}(1+2\cos\theta-8\cos^2\theta)d\theta + \frac{1}{2}\int_{\pi/2}^{\pi}(1+2\cos\theta+\cos^2\theta)d\theta\\ &=\frac{1}{2}\int_{\pi/3}^{\pi/2}(-3+2\cos\theta-4\cos(2\theta))d\theta + \frac{1}{4}\int_{\pi/2}^{\pi}(3+4\cos\theta+\cos(2\theta))d\theta\\ &=\frac{1}{2}(-3\cdot\frac{\pi}{6} + 2\cdot (1-\sqrt{3}/2) - 2\cdot (0-\sqrt{3}/2))+\frac{1}{4}(3\cdot \pi/2 + 4\cdot (-1) + 0)\\ &=\frac{1}{2}(2-\pi/2)+\frac{1}{4}(3\pi/2-4)\\ &=\frac{\pi}{8} \end{align} Doubling we get that the area of $D$ is $\dfrac{\pi}{4}$.
Monday, March 5, 2018 (Double integrals over general regions)
Exercise 1: Compute the double integral \[\int_0^1\int_0^{x^2}\frac{y}{x^5+1}\ dydx\] where $D=\{(x,y)\mid 0\leq x\leq 1, 0\leq y\leq x^2\}$.
Solution: First, we set up the double integral as an iterated integral as \[\int_0^1\int_0^{x^2}\frac{y}{x^5+1}\ dydx=\int_0^1\left(\int_0^{x^2}\frac{y}{x^5+1}\ dy\right)dx\] Next, we compute the middle integral \[\int_0^{x^2}\frac{y}{x^5+1}\ dy = \frac{y^2}{2(x^5+1)}|_0^{x^2}=\frac{x^4}{2(x^5+1)}\] Finally, we compute the outside integral \[\int_0^1\frac{x^4}{2(x^5+1)}dx = \frac{1}{2}\int_0^1\frac{x^4}{x^5+1}dx\] using the change of variables $u=x^5+1$ ($du=5x^4dx$) to get \[\frac{1}{2}\int_0^1\frac{x^4}{x^5+1}dx = \frac{1}{10}\int_1^{2}\frac{du}{u}=\frac{\ln(2)}{10}\]
Exercise 2: Reverse the order of integration in the double iterated integral \[\int_1^2\int_{1/x^2}^1f(x,y)dydx\]
Solution: The first thing to do is to sketch
the region. The region is given as a type 1 region with $1\leq
x\leq 2$ and $1/x^2\leq y\leq 1$. To write it as a type 2 region
note that the natural bounds on $y$ are $1/4\leq y\leq 1$.
Given $y$, what are now the bounds on $x$? The easiest is
to look at the sketch. Note that $x\leq 2$ and that $x\geq
1/\sqrt{y}$ which comes from $y\geq 1/x^2$.
Using this description of the region the double integral,
as an iterated integral, is
\[\int_{1/4}^1\int_{1/\sqrt{y}}^2f(x,y)dxdy\]
Exercise 3: Find the volume under the plane $x+y+z=2$ over the triangle with vertices $(0,0)$, $(1,0)$ and $(1,1)$.
Solution: Writing $D$ for the triangle we need to compute \[\iint_DzdA=\iint_D (2-x-y)dA\] The region $D$ is described by $0\leq x\leq 1$ and $0\leq y\leq x$. Again, we first set up the double integral as an iterated one. \[\iint_D(2-x-y)dA=\int_0^1\left(\int_0^x(2-x-y)dy\right)dx\] Next we compute the inside integral \[\int_0^x(2-x-y)dy = ((2-x)y-y^2/2) |_0^x = (2-x)x - x^2/2 = 2x-3x^2/2\] Finally we compute the outside integral \[\int_0^1 (2x-3x^2/2)dx = (x^2 - x^3/2)|_0^1 = 1/2\]
Friday, March 2, 2018 (Double integrals over rectangles)
Exercise 1: Compute the following integral \[\iint_R\sqrt{x+y}dA\] over the unit square $0\leq x,y\leq 1$.
Solution: The integral, as an iterated integral, is \begin{align*} \int_0^1\int_0^1\sqrt{x+y}dydx&=\int_0^1\left(\int_0^1\sqrt{x+y}dy\right)dx\\ &=\int_0^1 \left(\frac{2}{3}(x+y)^{3/2}|_0^1\right)dx\\ &=\frac{2}{3}\int_0^1 \left((1+x)^{3/2}-x^{3/2}\right)dx\\ &=\frac{2}{3}\left(\frac{2}{5}(1+x)^{5/2}-\frac{2}{5}x^{5/2}\right)|_0^1\\ &=\frac{4}{15}(2^{5/2}-2)\\ &=\frac{8(\sqrt{2}-1)}{15} \end{align*}
Exercise 2: Approximate the following integral \[\iint_R\sin(\pi x y)dA\] over the unit square $0\leq x,y\leq 1$ with $n=2$ using the lower left corners.
Solution: \[\frac{1}{4}\left(\sin 0+\sin 0+\sin 0+\sin(\pi/4)\right)=\frac{\sqrt{2}}{8}\]
Wednesday, February 28, 2018 (Lagrange multipliers with two constraints)
Exercise 1: Compute the min and max of the function $f(x,y,z)=x^2+y^2+z^2$ given the constraints $x-y=1$ and $y^2-z^2=1$.
Solution: The Lagrange multipliers system is \[\begin{cases} x-y=1\\ y^2-z^2=1\\ 2x=\lambda \\ 2y=-\lambda +2y\mu\\ 2z=-2z\mu \end{cases}\] In the last equation either $z=0$ or $\mu=-1$. If we assume $z\neq 0$ then $\mu=-1$ and equations 3 and 4 become $2x=\lambda$ and $2y=-\lambda+2y$ which give $x=\lambda/2$ and $y=-\lambda/4$. The first equation then yields $1=x-y = 3\lambda/4$ so $\lambda=4/3$ which gives $y=-1/3$. But then the second equation would give $1/9-z^2=1$ so $z^2=-8/9$ which is impossible. Therefore $z=0$. Then $y^2=1+z^2=1$ so $y=\pm 1$ and $x=1+y$. The two solutions are $(2,1,0)$ and $(0,-1,0)$. The former gives the min and the latter the max of the function.
Exercise 2: The total area of a box if 2250 and the total length of its sides is 240. Find the largest volume the box can have. Set up the problem. We'll solve the system together.
Solution: Write $x,y,z$ for the dimensions of the box. Then $g(x,y,z)=xy+yz+xz=1125 =2250/2$ and $h(x,y,z)=x+y+z=60=240/4$. The function is $V(x,y,z)=xyz$. The gradients are $\nabla V = \langle yz,xz,xy\rangle$, $\nabla g = \langle y+z, x+z, x+y\rangle$ and $\nabla h = \langle 1,1,1\rangle$. The system is therefore \[\begin{cases}xy+yz+zx=1125\\ x+y+z=60\\ yz=(y+z)\lambda + \mu\\ xz=(x+z)\lambda + \mu\\ xy=(x+y)\lambda + \mu\end{cases}\]
Monday, February 26, 2018 (Lagrange multipliers with one constraint)
Exercise 1: Suppose you want to minimize the function $f(x,y)=4-x^2-xy$ over the unit circle $x^2+y^2=1$. Set up the system of equations you'd need to solve using Lagrange Multipliers. Do not solve.
Solution: $\nabla f=\langle -2x-y,-x\rangle$ and $\nabla g=\langle 2x,2y\rangle$. The system is \[\begin{cases}x^2+y^2=1\\ \langle -2x-y,-x\rangle=\lambda \langle 2x,2y\rangle\end{cases}\] which, written out, is \[\begin{cases}x^2+y^2=1\\ -2x-y = \lambda \cdot 2x\\ -x=\lambda\cdot 2y\end{cases}\]
Exercise 2: To find the min and max of $f(x,y,z)=xyz$ over the ellipsoid $g(x,y,z)=x^2+2y^2+3z^2=6$ using Lagrange multipliers we saw that we need to solve the system \[\begin{cases} x^2+2y^2+3z^2=6\\ yz=\lambda\cdot 2x\\ xz=\lambda \cdot 4y\\ xy=\lambda\cdot 6z \end{cases} \] Solve this system and find all the points $(x,y,z)$ on the ellipsoid where $xyz$ might be min or max.
Solution: In class we noted that if $\lambda=0$ then at least two of the variables $x,y,z$ must be 0 and then $f(x,y,z)=0$. In fact if any of the variables $x,y,z$ satisfying the system is 0, the value of the function $xyz$ is 0 so we don't actually need to compute all solutions of this type. If $\lambda\neq 0$ and $x,y,z\neq 0$ we may divide equations 2 and 3, and then 2 and 4 to get \begin{align*} \frac{yz}{xz}&=\frac{2x}{4y}&\frac{yz}{xy}&=\frac{2x}{6z}\end{align*} which simplifies to \begin{align*} \frac{y}{x}&=\frac{x}{2y}&\frac{z}{x}&=\frac{x}{3z} \end{align*} Cross multiplying we get $x^2=2y^2=3z^2$. From the constraint we know that they add up to $6$ to $x^2=2y^2=3z^2=2$ which gives the 8 solutions \[(\pm\sqrt{2},\pm 1,\pm\sqrt{2/3})\] The minimum of $xyz$ is therefore $-2/\sqrt{3}$ while the maximum is $2/\sqrt{3}$.
Friday, February 23, 2017 (Extrema of functions on bounded regions)
Finding Local Extrema on a region with boundaries
- If $f(x,y)$ is a continuous function defined over a region $D$ with boundary its points of local extremum are located either at critical points in the interior of $D$ or along the boundary of $D$.
- (Not necessary for absolute extrema) Suppose $(a,b)$ is a point of local extremum in the
interior of $D$.
- If $f_{xx}(a,b)f_{yy}(a,b)\lt f_{xy}^2(a,b)$ then $(a,b)$ is a saddle point.
- If $f_{xx}(a,b)f_{yy}(a,b)\gt f_{xy}^2(a,b)$ and $f_{xx}(a,b)\gt 0$ then $(a,b)$ is a point of local minimum.
- If $f_{xx}(a,b)f_{yy}(a,b)\gt f_{xy}^2(a,b)$ and $f_{xx}(a,b)\lt 0$ then $(a,b)$ is a point of local maximum.
- In all other cases the test is inconclusive.
- To find the local extrema of $f(x,y)$ along the boundary the following sometimes works: use the equations defining the boundary to transform the two-variable function $f(x,y)$ into a single variable function. Then Use Calc 2 to find the min and max of this single variable function.
- To find the absolute minimum and absolute maximum it is not necessary to classify each critical point. Simply evaluate the function at all the critical points and pick out the min and max from the list of values at the critical point as well as the list of min and max along the boundary.
Exercise 1: We want an acquarium of 1 cubic yard volume. For aesthetic reasons the dimensions of the acquarium cannot be larger than 2 yards. The base of the acquarium costs 16 times more per unit area than the sides. The goal is to find the dimensions of the acquarium that minimize the cost. In this exercise simply set up the problem, but do not solve it. By this I mean write a function $f(x,y)$ to minimize over a region $D$, that you sketch in the plane.
Solution: Let $x$, $y$ be the dimensions of the base and $z$ the height. Then $xyz=1$ is the volume. The cost is \[C(x,y,z)=16xy + 2xz + 2yz\] with $xy$ the base area and $2xz+2yz$ the area of the four sides. As $z=1/(xy)$ we get the two-variable function \[C(x,y) = 16xy + 2x/xy+2y/xy = 16xy+2/x+2/y\] We need to minimize this cost function and we need to translate the constraints $x,y,z\leq 2$ into constraints on $x$ and $y$ only. As $z=1/(xy)$ the condition $z\leq 2$ becomes $xy\geq 1/2$. So we need to minimize $C(x,y)$ over the region $D$ described by $0\leq x,y\leq 2$ and $xy\geq 1/2$.
Thursday, February 22, 2018 (Tutorial) (Local extrema)
Finding Local Extrema
- If $f(x,y)$ is a continuous function its points of local extremum are located at critical points.
- Suppose $(a,b)$ is a point of local extremum.
- If $f_{xx}(a,b)f_{yy}(a,b)\lt f_{xy}^2(a,b)$ then $(a,b)$ is a saddle point.
- If $f_{xx}(a,b)f_{yy}(a,b)\gt f_{xy}^2(a,b)$ and $f_{xx}(a,b)\gt 0$ then $(a,b)$ is a point of local minimum.
- If $f_{xx}(a,b)f_{yy}(a,b)\gt f_{xy}^2(a,b)$ and $f_{xx}(a,b)\lt 0$ then $(a,b)$ is a point of local maximum.
- In all other cases the test is inconclusive.
- To find the absolute minimum and absolute maximum it is not necessary to classify each critical point. Simply evaluate the function at all the critical points and pick out the min and max from the list of values.
Exercise 1: Find the critical values of the function \[f(x,y) = x^2y e^{-x^2-y^2}\] and determine the absolute minimum and maximum values of $f(x,y)$.
Solution: The gradient is \[\nabla f(x,y)=\langle (2xy-2x^3y)e^{-x^2-y^2}, (x^2-2x^2y^2)e^{-x^2-y^2}\rangle\] so the critical points are those where $2xy=2x^3y$ and $x^2=2x^2y$. This is true when $x=0$ or, if $x\neq 0$, then for $y=\pm \dfrac{1}{\sqrt{2}}$ (from the second equation) and $x=\pm 1$ (from the first equation). The values of the function at the critical points are $f(0,y)=0$, $f(\pm 1, 1/\sqrt{2}) = e^{-3/2}/\sqrt{2}$ and $f(\pm 1, -1/\sqrt{2}) = -e^{-3/2}/\sqrt{2}$. When $x$ or $y$ is large, $e^{-x^2-y^2}$ is close to 0 and $f(x,y)$ is close to 0. Therefore the absolute minimum is attained at $(\pm 1, -1/\sqrt{2})$ and the absolute maximum at $(\pm 1, 1/\sqrt{2})$.
Wednesday, February 21, 2018 (Gradients, tangent planes)
Exercise 1: Consider the surface \[x^2+y^2+z^2=xyz+x+y+z+8\] Find the equation of the tangent plane at the point $(1,-2,1)$. [You ought to check that this point is on the surface or else the formula you are applying won't make sense.]
Solution: The surface is the level curve \[f(x,y,z)=x^2+y^2+z^2-xyz-x-y-z=8\] and the normal vector of the tangent plane is \[\nabla f=\langle 2x-yz-1, 2y-xz-1, 2z-xy-1\rangle\] At the point $(1,-2,1)$ this is just \[\nabla f(1,-2,1)=\langle 3, -6,3\rangle\] The tangent plane has normal vector $\langle 3,-6,3\rangle$ and passes through $(1,-2,1)$ so the equation is \[3(x-1)-6(y+2)-3(z-1)=0\]
Exam 1 Review, Monday, February 19, 2018
Vectors:
- Find the volume of the parallelopiped determined by the vectors $\langle 6,3,1\rangle$, $\langle 99,2,0\rangle$ and $\langle 7,0,0\rangle$. (Answer: 14.)
- Suppose $|a|=4,|b|=6$ and the angle between the vectors is $\pi/6$. Find $a\cdot b$. (Answer: $12\sqrt{3}$.)
- Find a unit vector in the direction of $\langle 2,-1,-2\rangle$. (Answer: $\langle 2,-1,-2\rangle/3$.)
- For $a=\langle 1,3,5\rangle$, $b=\langle 1,1,-1\rangle$ find $\operatorname{proj}_ab$. (Answer: $\langle -1,-3,-5\rangle/35$.)
Lines, planes, and surfaces:
- Find the line of intersection between $2x+y-z=10$ and $y+2z=7$. (Answer: $\langle x,y,z\rangle=\langle 3t,9-4t, -1+2t\rangle$ or $\dfrac{x}{3}=\dfrac{y-9}{-4}=\dfrac{z+1}{2}$.)
- Find the equation of the plane through $(5,2,0)$, $(3,-1,6)$ and $(1,3,2)$ and compute the area of the parallelogram determined by the first two vectors. (Answer: Plane is $-12(x-5)-20(y-2)-14z=0$ and area is $\sqrt{740}$.)
- Find a symmetric equation for the line through $(1,2,3)$ perpendicular to the plane $x-5y = 7$. (Answer: $\dfrac{x-1}{1}=\dfrac{y-2}{-5}$ and $z=3$.)
- Find the distance form the point $(3,-3,6)$ to the plane $2x-y-2z+14=0$. (Answer: $11/3$.)
Vector functions and motion in space:
- Find the integral of the function $f(t)=\langle \cos(t), \ln(t), 1/\sqrt{1-t^2}\rangle$. (Answer: $\langle \sin(t), t(\ln(t)-1), \arcsin(t)\rangle+\vec{C}$.)
- Find $T,B,N, a_T, a_N$ and equations for the normal and osculating plane for $r(t)=\langle e^t, \sqrt{2}t, e^{-t}\rangle$ at $t=0$. (Answer: $T=\langle 1,\sqrt{2},-1\rangle/2$, $B=\langle 1, -\sqrt{2}, -1\rangle/2$, $N=\langle \sqrt{2},0, \sqrt{2}\rangle/2$, $a_T=T\cdot a=0$ and $a_N=\sqrt{|a|^2-a_T^2}=\sqrt{2}$.)
- If $v(t)=\langle e^t,e^{-t}, \cos(t)\rangle$ find $r(t)$ knowing that $r(0)=\langle 1,1,0\rangle$. (Answer: $r(t)=\langle e^t,2-e^{-t},\sin(t)\rangle$.)
- Find the tangent line to $f(t)=\langle \ln(t+1), e^t, t^3\rangle$ at $t=1$ and determine if it contains the point $(\ln(2)+1, 3e, 7)$. (Answer: Tangent line symmetric equation is $\dfrac{x-\ln(2)}{1/2}=\dfrac{y-e}{e}=\dfrac{z-1}{3}$ and so it does contain the point.)
Gradients and partial derivatives:
- $x,y,z$ are defined implicitly by $xyz=\sin(x+y+z)$. Find $\partial x/\partial y$. (Answer: $-\dfrac{\cos(x+y+z)-xz}{\cos(x+y+z)-yz}$.)
- Determine if the limit \[\lim_{(x,y)\to (0,0)}\frac{7x^4y^4}{x^2+y^2}\] exists. If it does, compute it. (Answer: The limit is 0.)
- Knowing that $f(x,y,z)=xy^2z^3$, $x=\sin(st)$, $y=s^2-t^2$ and $z=s/t$ compute $\partial f/\partial s$. (Answer: $y^2z^3t\cos(st)+4xyz^3s+3xy^2z^2/t$.)
- Find the direction of largest decrease for the function \[f(x,y)=1-x^2-2xy^3\] at the point $(2,-1)$. (Answer: It's the unit vector in the direction $-\nabla f(2,-1)=\langle 2, 12\rangle$, i.e., $\vec{u}=\langle 2, 12\rangle/\sqrt{148}$.)
Friday, February 16, 2018 (Gradients)
Exercise 1: Find the direction of largest decrease for the function \[f(x,y)=1-x^2-2xy^3\] at the point $(2,-1)$.
Solution: The gradient is $\nabla f=\langle -2x-2y^3,-6xy^2\rangle$ and at the point $(2,-1)$ this is simply $\nabla f(2,-1)=\langle -2, -12\rangle$. Going in the direction $\vec{u}=\nabla f$ leads to fastest increase and going in the direction $\vec{u}=-\nabla f = \langle 2,12\rangle$ leads to fastest decrease.
Wednesday, February 14, 2018 (The chain rule)
Exercise 1: An example inspired from economics. You know \begin{align*}P&=K^{1/3}L^{2/3}\\ K&=\frac{10+t}{(1+r)^2}\\ L&=100+\frac{t}{1+r} \end{align*} Compute $\dfrac{\partial P}{\partial t}$.
Solution: First draw the diagram and write the chain rule \[\partial P/\partial t = P_KK_t+P_LL_t\] Then compute \begin{align*} P_K&=1/3(L/K)^{2/3}\\ P_L&=2/3(K/L)^{1/3}\\ K_t&=1/(1+r)^2\\ L_t&=1/(1+r) \end{align*} so \[P_t=\frac{(L/K)^{2/3}}{3(1+r)^2}+\frac{2(K/L)^{1/3}}{3(1+r)}\]
Monday, February 12, 2018 (Partial derivatives, implicit differentiation)
Exercise 1: Find $f_x$, $f_y$, $f_{xx}$, $f_{xy}$, $f_{yx}$ and $f_{yy}$ for the function \[f(x,y)=x^y\]
Solution: First we compute the first derivatives \begin{align*} f_x&=\partial_x (x^y) = yx^{y-1}\\ f_y&=\partial_y(x^y) = x^y\ln(x) \end{align*} Now \begin{align*} f_{xx}&=\partial_x(f_x)=\partial_x(yx^{y-1})\\&=y(y-1)x^{y-2}\\ f_{xy}&=\partial_y(f_x)=\partial_y(yx^{y-1})\\&=x^{y-1}+yx^{y-1}\ln(x)\\ f_{yx}&=\partial_x(f_y)=\partial_x(x^y\ln(x))\\&=yx^{y-1}\ln(x)+x^y\cdot\frac{1}{x}=yx^{y-1}\ln(x)+x^{y-1}\\ f_{yy}&=\partial_y(f_y)=\partial_y(x^y\ln(x))\\&=x^y\ln^2(x) \end{align*}
Exercise 2: Consider the equation \[x^2+y^2+z^2=1\] Compute implicitly the double partial derivative $z_{xy}$.
Solution:
First solution: (Using direct implicit
differentiation) Take $\partial/\partial_x$ and find that
\[2x +2z z_x = 0\]
so $z_x=-\dfrac{x}{z}$. If you repeat this operation with
$\partial/\partial_y$ you get $z_y = -\dfrac{y}{z}$.
Now
\[z_{xy} = \frac{\partial}{\partial y}z_x =
\frac{\partial}{\partial y}-\frac{x}{z} = \frac{x z_y}{z^2}\]
using the chain rule for differentiating with respect to $y$
treating $z$ as a function and $x$ as a constant. Finally
\[z_{xy}=\frac{xz_y}{z^2} = -\frac{xy}{z^3}\]
by substituting our previously computed formula for $z_y$.
Second solution: (This second solution
uses the chain rule, which we'll see next lecture) Taking partial wrt $x$ get
\[z_x = -\frac{F_x}{F_z}=-\frac{x}{z}\]
where $F(x,y,z)=x^2+y^2+z^2-1$. Now taking partial wrt $y$ we
get
\[z_{xy} = -\partial_y\frac{x}{z}=\frac{x z_y}{z^2}\]
using the chain rule, $x$ being treated as a constant. Finally
we compute
\[z_y=-\frac{F_y}{F_z}=-\frac{y}{z}\]
so
\[z_{xy}=-\frac{xy}{z^3}\]
Friday, February 9, 2018 (Limits)
Exercise 1: Consider the limit \[\lim_{(x,y,z)\to (0,0,0)}\frac{xy+y^3+z^3}{x^2+y^2+z^2}\] If the limit exists compute it. If not, why not? [Hint: It does not.]
Solution: The limit does not exist. Approaching from the direction $x=y=0$ and $z\to 0$ gives the directional limit \[\lim_{x=y=0,z\to 0}\frac{xy+y^3+z^3}{x^2+^2+z^2}=\lim_{z\to 0}\frac{z^3}{z^2}=\lim_{z\to 0}z=0\] However, approaching from the direction $x=y\to 0$ and $z=0$ gives the directional limit \[\lim_{x=y\to 0,z=0}\frac{xy+y^3+z^3}{x^2+^2+z^2}=\lim_{x\to 0}\frac{x^2+x^3}{2x^2}=\lim_{x\to 0}(1+x)/2=1/2\] As the two limits differ the limit as $(x,y,z)\to (0,0,0)$ does not exist.
Exercise 2: Does the limit \[\lim_{(x,y)\to (0,0)}\frac{xy^4}{x^2+y^8}\] exist? [Hint: no.]
Solution: Going in the direction $y=0$ and $x\to 0$ we get \[\lim_{y=0,x\to 0}\frac{xy^4}{x^2+y^8}=\lim_{x\to 0}\frac{x\cdot 0}{x^2+0^8}=0\] For a different value of the limit we need to try something more dramatic than going along an axis, or even just lines. The idea is to make the denominator simple, and the sum $x^2+y^8$ is simple when $x^2=y^8$. Let's take $x=y^4\to 0$. Then \[\lim_{x=y^4\to 0}\frac{xy^4}{x^2+y^8}=\lim_{y\to 0}\frac{y^8}{2y^8}=\frac{1}{2}\] As they are different the limit doesn't exist.
Exercise 3: Compute the limit \[\lim_{(x,y)\to (0,0)}\frac{x^2y^2}{x^2+y^2}\] exist? [Hint: no.]
Solution: \begin{align*}\lim_{(x,y)\to (0,0)}\frac{x^2y^2}{x^2+y^2}&=\lim_{(x,y)\to (0,0)}\frac{1}{\frac{x^2+y^2}{x^2y^2}}\\ &=\lim_{(x,y)\to (0,0)}\frac{1}{\frac{1}{y^2}+\frac{1}{x^2}}\\ &=\lim_{(x,y)\to (0,0)}\frac{1}{\infty+\infty}=0 \end{align*}
Wednesday, February 7, 2018 (Functions of two or three variables)
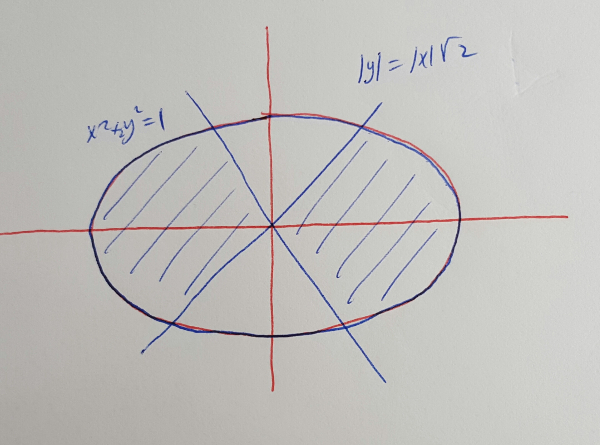
Exercise 1: What is the domain of the two-variable function \[f(x,y)=\ln(1-x^2-2y^2)+\sqrt{2x^2-y^2}\]
Solution: For $\ln(A)$ to make sense you
need $A>0$ and for $\sqrt{A}$ to make sense you need $A\geq
0$. So the domain is the set of all $(x,y)$ satisfying
\begin{align*}1-x^2-2y^2&\gt 0\\
2x^2-y^2&\geq 0
\end{align*}
which can be rewritten as
\begin{align*}x^2+2y^2&\lt 1\\
|y|&\leq |x|\sqrt{2}
\end{align*}
This completely answers the question as stated. But suppose we
wanted to shade the region in the plane corresponding to the
domain. First, draw the curves corresponding to the cases of
equality, namely the ellipse $x^2+2y^2=1$ and the two lines
$|y|=|x|\sqrt{2}$, the two lines being $y=\pm x\sqrt{2}$. These
curves cut up the plane into regions and you can test each
region by simply choosing a point inside the region and
verifying if it is in the domain. This way you get the regions
on the left and right of the two lines and inside the ellipse.
Exercise 2: Which of the following functions has the contour plot
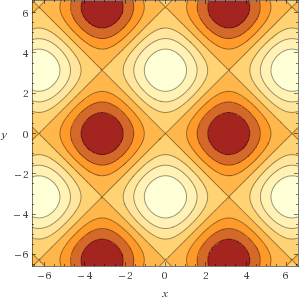
Solution: The function is $\cos(x)-\cos(y)$. It is periodic so that rules out options 3 and 5. It is periodic in two directions so that rules out option 1. Finally, it is constant along diagonal lines (from the picture) and $\cos(x)-\cos(y)$ is constant along $x=y$ whereas $\sin(xy)$ would be constant along hyperbolae $xy=\textrm{const}$.
Monday, February 5, 2018 (Motion in space)
Exercise 1: A curve $\vec{r}(x)=\langle x+2, 1-x, x^2/2\rangle$. Find an equation for the osculating plane at $x_0$.
Solution: Once we know a point and a normal vector we can find the equation of the plane. First, the point on the plane is \[\vec{r}(x_0)=(x_0+2, 1-x_0, x_0^2/2\rangle\] Next, a normal vector is \[\vec{b}=\vec{r}'(x_0)\times\vec{r}''(x_0)\] which we compute as \begin{align*}\vec{r}'(x_0)&=\langle 1,-1,x_0\rangle\\ \vec{r}''(x_0)&=\langle 0,0,1\rangle \end{align*} and so \[\vec{b}=\langle -1,-1,0\rangle\] We can now write the equation of the plane as \[-(x-(x_0+2)) - (y - (1-x_0)) = 0\]
Exercise 2: A particle moves along the curve \[\vec{r}(t)=\langle \sin(t), \cos(t), t/\pi\rangle\] Where should the particle leave the curve in order to arrive, by momentum, at the point $(\sqrt{3}, -1, 1/3+\sqrt{3}/\pi)$?
Solution: As in the example in class we seek the time $t$ such that if we leave the curve at that time then the direction of (inertial) motion will take us to the desired destination. The direction of motion is given by velocity $\vec{v}(t)$ whereas the direction of desired motion is exactly $\langle \sqrt{3}, -1, 1/3+\sqrt{3}/\pi\rangle - \vec{r}(t)$ (destination minus current position). Mathematically this amount to saying that $\vec{v}(t)=\langle \cos(t),-\sin(t), 1/\pi\rangle$ is parallel to \[\langle \sqrt{3}, -1, 1/3+\sqrt{3}/\pi\rangle - \vec{r}(t)=\langle \sqrt{3}-\sin(t), -1-\cos(t), 1/3+\sqrt{3}/\pi-t/\pi\rangle\] The two vectors are parallel when one is a scalar multiple of the other so we compute the coordinate-by-coordinate ratios and set them all equal: \[\frac{\sqrt{3}-\sin(t)}{\cos(t)}=\frac{-1-\cos(t)}{-\sin(t)}=\frac{1/3+\sqrt{3}/\pi-t/\pi}{1/\pi}\] From the first equation we get \begin{align*}(\sqrt{3}-\sin(t))\cdot(-\sin(t))&=\cos(t)\cdot (-1-\cos(t))\\ -\sqrt{3}\sin(t)+\sin^2(t)&=-\cos(t)-\cos^2(t)\\ 1=\sin^2(t)+\cos^2(t)&=\sqrt{3}\sin(t)-\cos(t) \end{align*} so we have to solve \[\sqrt{3}\sin(t)-\cos(t)=1\] Here you need to use your knowledge of trig functions and how to solve equations of this form that you learned in Calc 2. Divide by 2 and get \begin{align*}\frac{\sqrt{3}}{2}\sin(t)-\frac{1}{2}\cos(t)&=\frac{1}{2}\\ \cos(\pi/6)\sin(t)-\sin(\pi/6)\cos(t)&=\sin(\pi/6)\\ \sin(t-\pi/6)&=\sin(\pi/6) \end{align*} so we get $t-\pi/6 = \pi/6$ (there's actually infinitely many solutions of the form $t-\pi/6=\pi/6 + 2\pi n$ and $t-\pi/6 = (2n+1)\pi - \pi/6$ but we only want one solution) so $t=\pi/3$ works. If you let go at $t_0=\pi/3$ then your motion at time $t>t_0$ will be \[\vec{r}_{new}(t) = \vec{r}(\pi/3) + \vec{v}(t_0)(t-\pi/3)\] in other words \[\vec{r}_{new}(t) = \langle \sqrt{3}/2, 1/2, 1/3\rangle + (t-\pi/3)\langle 1/2, -\sqrt{3}/{2}, 1/\pi\rangle\] and at time $t=\pi/3+\sqrt{3}$ the particle arrives at the desired destination.
Exercise 3: A particle's position in space at time $t$ is given by \[\vec{r}(t)=\langle 2t, t^2, t^3/3\rangle\] If the particle starts at time $t=0$, where will the particle be after having moved 15 units?
Solution: Recall that distance traveled from time 0 to time $t$ is \[s(t)=\int_0^t|\vec{r}'(x)|dx\] so we first compute this integral. \begin{align*}\vec{r}'(t)&=\langle 2, 2t, t^2\rangle\\ |\vec{r}'(t)|&=\sqrt{4+4t^2+t^4}=\sqrt{(2+t^2)^2}=2+t^2\\ s(t)&=\int_0^t (2+x^2)dx=2t+t^3/3 \end{align*} We are now asked where the particle was when $s(t)=15$. First we solve \[s(t)=t^3/3+2t=15\] which we can multiply by 3 to get $t^3+6t-45=0$. We can factor this \[t^3-6t-45 = t^3-27 + 6t-18 = (t-3)(t^2+3t+9)+6(t-3) = (t-3)(t^2+3t+15) = 0\] whose only solution is $t=3$ so only at $t=3$ has the particle traversed 15 units of distance. Its location at this time is \[\vec{r}(3)=\langle 6, 9, 9\rangle\]
Friday, February 2, 2018 ($T,N,B$ frame)
The TNB frame moving along the trefoil knot (textbook page
891) $\langle (2+\cos 1.5 t)\cos t, (2+\cos 1.5t)\sin t, \sin 1.5
t\rangle$. T is red, N is green and B is blue.

Exercise 1: The curve \[\vec{r}(t)=\langle \sin(3t), \cos(3t), 4t\rangle\] is a helix. Find $\vec{T}$, $\vec{B}$ and $\vec{N}$ at $t=\pi/18$.
Solution: You can do this at time $t=\pi/18$ but I'll write it up at all $t$ and then plug in $t=\pi/18$. \begin{align*}v(t)&=r'(t)=\langle 3\cos(3t), -3\sin(3t), 4\rangle\\ |v(t)|&=\sqrt{3^2(\sin^2(3t)+\cos^2(3t))+4^2}=5\\ T(t)&=v(t)/|v(t)|=\langle\frac{3}{5}\sin(3t), \frac{3}{5}\cos(3t), \frac{4}{5}\rangle\\ a(t)&=v'(t)=\langle -9\sin(3t), -9\cos(3t), 0\rangle\\ b(t)&=v(t)\times a(t) = \langle 36\cos(3t), -36\sin(3t), -27\rangle\\ &= 9\langle 4\cos(4t), -4\sin(3t), 3\rangle\\ |b(t)|&=45\\ B(t)&=b(t)/|b(t)| = \langle \frac{4}{5}\cos(3t), -\frac{4}{5}\sin(3t), -\frac{3}{5}\rangle\\ \end{align*} Now we plug in $t=\pi/18$ to get \begin{align*}T(\pi/18)&=\langle \frac{3\sqrt{3}}{10}, -\frac{3}{10}, \frac{4}{5}\rangle\\ B(\pi/18)&=\langle\frac{2\sqrt{3}}{5}, -\frac{2}{5}, -\frac{3}{5}\rangle\\ N(\pi/18)&=B(\pi/18)\times T(\pi/18)\\ &=\langle -\frac{1}{2}, -\frac{\sqrt{3}}{2}, 0\rangle \end{align*}
Exercise 2: For the curve from Exercise 1 find at time $t$ the normal and tangential components of acceleration.
Solution: We apply the formulae from class and the computations from the previous exercise. \begin{align*} a_T(t)&=\frac{v(t)\cdot a(t)}{|v(t)|}\\ &=0\\ a_N(t)&=\sqrt{|a(t)|^2-a_T(t)^2}\\ &=|a(t)|\\ &=9 \end{align*} One can interpret $a_T=0$ as saying that the particle accelerates only in the normal direction.
Wednesday, January 31, 2018 (Vector integrals and derivatives)
Exercise 1: Compute the vector integral \[\int\langle t e^{2t}, \frac{t}{1-t}, \frac{1}{\sqrt{1-t^2}}\rangle dt\] [Hint: This is just Calc 2.]
Solution: This is an exercise in Calc 2. For the first integral use integration by parts: \begin{align*} \int t e^{2t} &= \int t d e^{2t}/2 \\ &= t e^{2t}/2 - \int e^{2t}/2 dt \\ &= t e^{2t}/2 - e^{2t}/4 + c \end{align*} For the second integral we first do long division to write \[\frac{t}{1-t}=\frac{1}{1-t}-1\] and then \[\int \frac{tdt}{1-t}=\int \frac{dt}{1-t}-\int dt = -\ln(1-t) - t + c\] Finally \[\int\frac{dt}{\sqrt{1-t^2}}=\arcsin(t)+c\] so \[\int\langle t e^{2t}, \frac{t}{1-t}, \frac{1}{\sqrt{1-t^2}}\rangle dt=\langle t e^{2t}/2 - e^{2t}/4, -\ln(1-t)-t, \arcsin(t)\rangle + \vec{C}\]
Monday, January 29, 2018 (Parametrizations of vector curves)
Exercise 1: Find a parametric equation for the curve given by the intersection of the cylinder $x^2+4y^2=4$ and the graph of the function $z=xy$.
Solution: We parametrize the cylinder as follows. Divide by $4$ to get $x^2/4 + y^2=1$ and then use trig substitutions. Write $x/2=\cos t$ and $y=\sin t$ in which case $x^2/4+y^2=\cos^2t+\sin^2t=1$. What is the third coordinate? $z=xy=2\cos t\sin t = \sin(2t)$. So the curve of intersection has parametric equation \[\vec{r}(t)=\langle 2\cos t, \sin t, \sin(2t)\rangle \]
Exercise 2: Find the point where the space curve given parametrically by $\vec{f}(t)=\langle t^2,t,t\rangle$ intersects the surface $x^2+4y^2=z^4$.
Solution: The coordinates of the particle at time $t$ are $x=t^2$, $y=t$ and $z=t$. To check whether the particle hits the surface we verify $x^2+4y^2=z^4$ which gives $t^4+4t^2=t^4$. This only happens when $t=0$. To find the actual point of intersection we ask: where was the particle at the time when it hit the surface. It was at $\vec{f}(0)=\vec{0}$.
Friday, January 26, 2018 (Distance from point to plane)
Exercise 1: Find the distance between the plane $x+2y+3z=4$ and the line $x=t, y=5-2t, z=12+t$ (you should also verify that they are parallel, but for the distance computations you may take this for granted).
Solution: The normal vector is $\vec{n}=\langle 1,2,3\rangle$ while the vector of the line is $\vec{v}=\langle 1,-2,1\rangle$. As $\vec{v}\cdot \vec{n}=0$ the line is perpendicular to the normal vector and therefore the line is parallel to the plane. Now pick ANY point on the line, say $t=0$ yielding $(0,5,12)$. The distance from the line to the plane is the same as the distance from this point to the plane. The distance is then \[\frac{|1\cdot 0 + 2\cdot 5+3\cdot 12 - 4|}{\sqrt{1^2+2^2+3^2}}=\frac{42}{\sqrt{14}}\]
Exercise 2: Find the parametric equation of the line passing through the point $(0,1,2)$, parallel to the plane $x+y+z=2$ and perpendicular to the line $x=1+t, y=1-t, z=2t$.
Solution: The plane has normal vector $\vec{n}=\langle 1,1,1\rangle$ and the line has vector $\vec{v}=\langle 1,-1,2\rangle$. We seek a line parallel to the plane and perpendicular to the line, so a line perpendicular to both $\vec{n}$ and $\vec{v}$. A vector of this line can be obtained by computing the cross product: \[\vec{a}=\vec{n}\times\vec{v}=\langle 3,-1,-2\rangle\] Our desired line will have vector $\langle 3,-1,-2\rangle$ and will contain the point $(0,1,2)$ so the parametric equation of this line is \[\vec{r}(t)=\langle 3t, 1-t, 2-2t\rangle\]
Thursday, January 25, 2018 (Tutorial) (Intersections of lines and planes)
Exercise 1: Find the intersection between the line $\langle 1-t, 2+3t, 6-2t\rangle$ with the plane $2x-y+z=13$.
Solution: At time $t$ the particle has coordinates $(x,y,z)=(1-t,2+3t,6-2t)$. To check whether at this time the particle is on the plane, we simply verify if $2x-y+z=13$. So \[2x-y+z=2(1-t)-(2+3t)+6-2t = 6-7t=13\] which gives $t=-1$. So at time $t=-1$ the particle was on the plane. Its position, which is the intersection of the line with the plane, was $(x,y,z)=(2, -1, 8)$.
Exercise 2: Are the lines \[\frac{x-1}{2}=\frac{y-2}{3}=\frac{z-3}{4}\] and \[\frac{x+1}{5}=\frac{y+6}{-3}=\frac{z-11}{-1}\] skew?
Solution: The vectors $\langle 2, 3, 4\rangle$ and $\langle 5, -3, -1\rangle$ are not parallel so the two lines are not parallel. Now we seek the point of intersection as in class. Write $t$ for time for the first line and $s$ for time for the second line, yielding the parametric equations $\langle 1+2t, 2+3t,3+4t\rangle$ and $\langle -1+5s, -6-3s, 11-s\rangle$. We seek to solve the system \[\begin{cases}1+2t=-1+5s\\2+3t=-6-3s\\3+4t=11-s\end{cases}\] The last equation gives $s=8-4t$. Plugging this into the first equation gives $1+2t=-1+5s = -1+5(8-4t)=-20t+39$ so $22t=38$ which gives $t=19/11$. Then $s=8-4t = 12/11$. These two values satisfy the first and third equations. Do these verify the second equation as well? Plug in: $2+3t = 79/11$ but $-6-3s=-102/11$ so the two lines are skew as there is no point of intersection.
Wednesday, January 24, 2018 (Coplanar vectors, areas, volumes)
Summary:
- Area of parallelogram spanned by $\vec{a},\vec{b}$ is $|\vec{a}\times\vec{b}|$.
- Volume of parallelepiped $\vec{a},\vec{b},\vec{c}$ is $|\vec{a}\cdot (\vec{b}\times\vec{c})|$.
- Distance from tip of $\vec{c}$ to plane spanned by $\vec{a}, \vec{b}$ is $\dfrac{|\vec{c}\cdot(\vec{a}\times\vec{b})|}{|\vec{a}\times\vec{b}|}$.
Exercise 1: Determine if the vectors $\vec{a}=\langle -4,2,4\rangle$, $\vec{b}=\langle 2,1,-2\rangle$ and $\vec{c}=\langle -3,4,1\rangle$ are coplanar.
Solution: First, compute $\vec{b}\times\vec{c}=\langle 9,4,11\rangle$ and then the volume of the parallelopiped $\vec{a}\cdot (\vec{b}\times\vec{c})=\langle -4,2,4\rangle\cdot \langle 9,4,11 \rangle=-4\cdot 9+2\cdot 4+4\cdot 11=16$ so the three vectors are not coplanar.
Exercise 2: Find the area of the triangle whose vertices are $P=(1,5,-2)$, $Q=(3,-1,0)$ and $R=(5,9,-2)$ and find the distance from the origin to the plane of the triangle.
Solution: We need the area of the triangle whose sides are the vectors $\vec{a}=\vec{PQ}=\langle 2,-6,2\rangle$ and $\vec{b}=\vec{PR}=\langle 4,4,0\rangle$. This area is $|\vec{a}\times\vec{b}|/2 = |\langle -8,8,32\rangle|/2=12\sqrt{2}$. The vector from $P$ to the origin is $\vec{c}=\langle -1,-5,2\rangle$ and the distance is then \[dist = \frac{|\vec{c}\cdot (\vec{a}\times\vec{b})|}{|\vec{a}\times\vec{b}|}=\] \[=\frac{|\langle -1,-5,2\rangle\cdot \langle -8,8,32\rangle|}{24\sqrt{2}}=\frac{32}{24\sqrt{2}}=\frac{2\sqrt{2}}{3}\]
Friday, January 19, 2018 (Dot product, cross product, angles)
Exercise 1: Suppose $\vec{a}$ and $\vec{b}$ are two vectors such that $\vec{a}\cdot \vec{b}=\sqrt{3}$ and $\vec{a}\times\vec{b}=\langle 1,2,2\rangle$. Find the angle between $\vec{a}$ and $\vec{b}$.
Solution: We know from class that $\vec{a}\cdot\vec{b}=|\vec{a}||\vec{b}|\cos(\theta)$ and also that $|\vec{a}\times\vec{b}|=|\vec{a}||\vec{b}|\sin(\theta)$. Dividing we see that \[\tan(\theta)=\frac{\sin(\theta)}{\cos{\theta}}=\frac{|\vec{a}||\vec{b}|\sin(\theta)}{|\vec{a}||\vec{b}|\cos(\theta)}=\] \[=\frac{|\vec{a}\times\vec{b}|}{\vec{a}\cdot\vec{b}}=\frac{|\langle 1,2,2\rangle|}{\sqrt{3}}=\frac{3}{\sqrt{3}}=\sqrt{3}\] from where we deduce that $\theta=\pi/3$.