Solution To Monty Hall Problem
It is easy to see that when the contestant makes his/her first choice of one of the three doors, without any prior information, that the probability that the car is behind the chosen door is 1/3. Now the contestant makes a further choice between switching doors or changing doors. The probabilities can best be calculated with a tree diagram.
Game Rules:
1. Pick a door. The diagram below shows the chances that you will pick the door with the car or either of the goats, Goat A or Goat B.
2. The host then reveals a goat behind one of the remaining doors. This of corse means that if you switch doors, you will not choose the open one, so if you decide to switch, there is just one door to choose from.
3. You decide whether you want to switch doors or stay with the one you chose. The probability that the car is behind the door unopened by your host depends on which choice you made originally. If the car is behind the door you chose first, the probability that it is behind the other door is 0. If the door you chose first has a goat behind it, then the car is most definitely behind the other door, and the probability that it is behind the door left unopened by your host is 1.
This gives us the probabilities in the tree diagrams below. We have one tree diagram to describe the situatuion when we switch doors and one to describe the situation when we stay with our original choice.
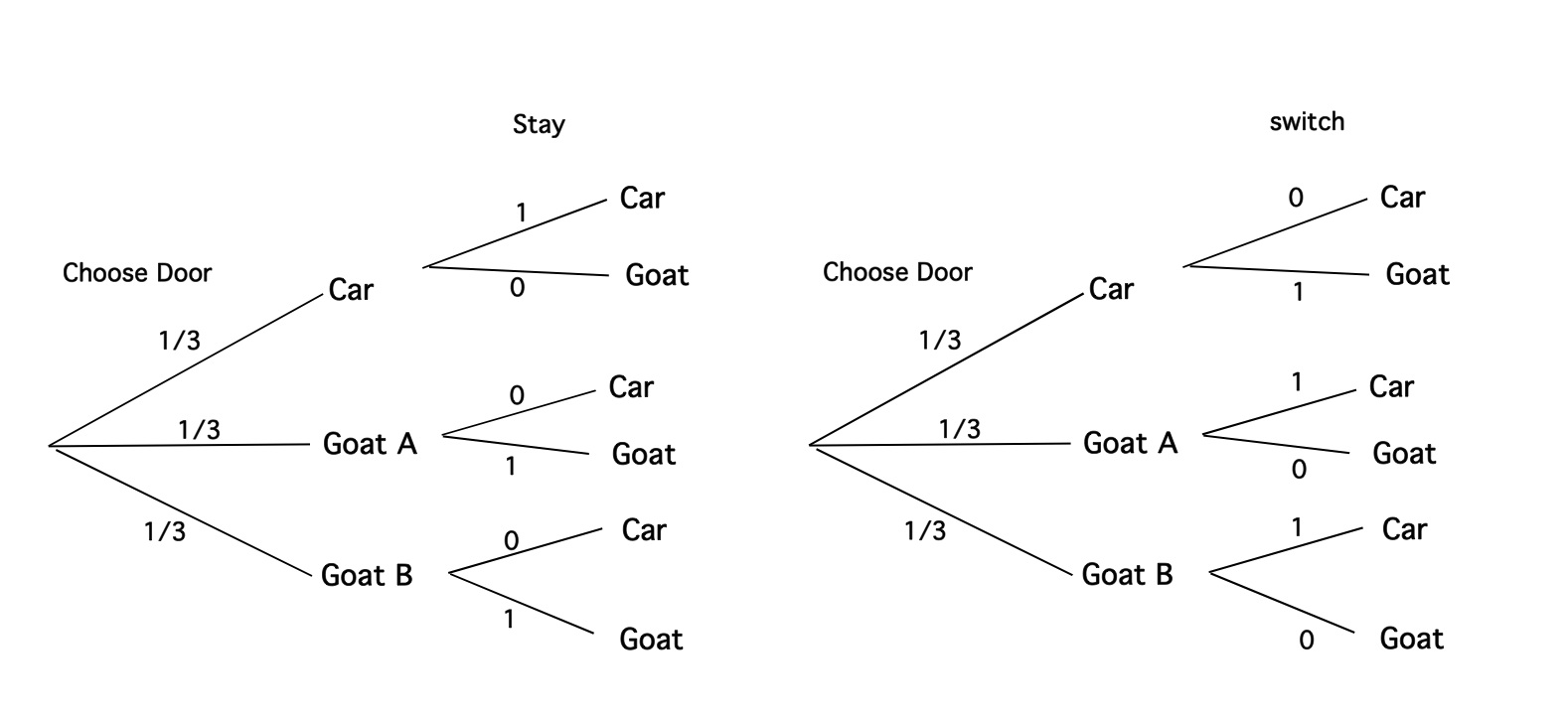
Hence we see that the chances of winning the car if we switch are 2/3 and the chances of winning the car if we stay with our original choice are 1/3.