Goal: This case introduces various descriptive statistics generated by FORECASTX^TM to make statistical inference on monthly rates of return for the Dow Jones 30 Index. Specifically, students will test whether monthly stock returns follow a normal probability distribution and make probability statements about the behavior of stock returns. Specifically, this case introduces:

• How to generate Descriptive Statistics in FORECASTX^TM
• Testing whether Stock Rates-of-Return are Normally Distributed
• Making Statistical Inference using the Standard Normal Distribution.
• Forecasting losses on the Stock Market.

The spreadsheet for this problem is CH2_Case1.xls. It contains the following data:

The series FSDJ is the monthly Dow Jones 30 Stock Index.

The series %FSDJ is the percentage change in the Dow Jones 30 Index. This was computed using a spreadsheet as follows:

Here we have used a log transformation converting our stock index data into continuously compounded rates of return, a common assumption in the finance literature.

Financial economists have long sought to define the return generating process of asset prices. Specifically, are monthly stock returns normally distributed? If so, all the information we need to make probability statements about future stock returns is the mean and variance using the standard normal distribution

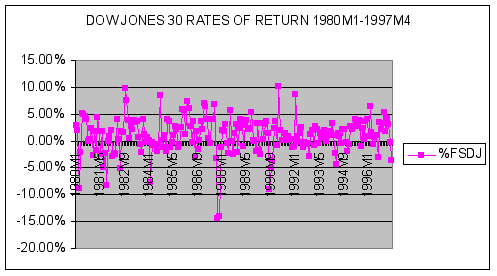
We can plot the monthly %FSDJ series using Excel’s Chart Menu. A time-series plot of the data is reported below.

Note that while monthly percentage rates of return are quite random, they appear to average slightly above zero and cluster around the mean.

To check this assertion further, we generated a frequency distribution of %FSDJ using Excel. The result is the following bar chart of Dow Jones rates of return:

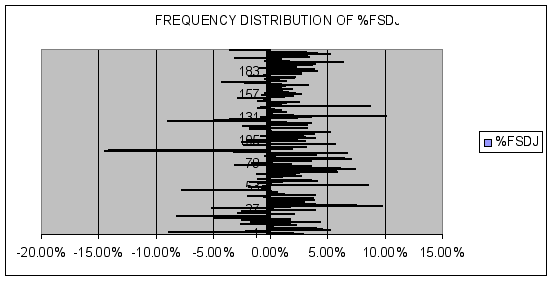
Considering the plots above, stock rates of return cluster around the average monthly rate of return of .997%, and can therefore be approximated by the normal probability distribution

Before we proceed to formally test our return data for normality, we can explore some of the implications of assuming stock rates of return are normally distributed. The key benefit is simplicity, in that if we know the mean (measure of location) and variance (measure of dispersion) of a normally distributed random variable then we know completely the behavior of such a variable from its probability distribution function. To see this point we will make a simple forecast regarding the probability of a loss, in any given month, on the Dow Jones 30 Industrials Index.

To generate various descriptive statistics using FORECASTX^TM, simply highlight %FSDJ in the CH2_Case1.xls spreadsheet and then open FORECASTX^TM. Choose a forecast horizon of zero since we are seeking to examine sample summary statistics. Access the Statistics Menu and select Mean, Median, Standard Deviation, Variance; then proceed to the More Menu and add Max, Min, Kurtosis, Skewness, and Mode. These summary statistics are reported in the FORECASTX^TM report below. (Note these values are rounded up relative to those used in the calculations below).

Question #1: Based upon the estimated monthly mean rate of return, calculate the mean annual rate of return over the sample period noting that your data is monthly.

The annual rate of return is found by multiplying the mean monthly return by 12. The mean monthly return on the Dow was .009974. Accordingly, the annual return is 12 times the monthly average, which is 12(.009974) = .119688 or about 12%. This reflects the historical annual rate of return earned on the Dow over 1980M1-1997M4.

Question #2: Given that annual standard deviation is the preferred measure of risk in finance, how risky is the Dow Jones index?

ANSWER:

On way to examine stock market behavior is in the context of classical statistics. Specifically, if stock rates of return follow a normal probability distribution, all behavior is summarized in the mean and variance. Accordingly, using the standard normal probability distribution we can make probability statements about the behavior of stock rates of return.

Question #3: Given the descriptive statistics reported above, what is the probability that, in any given month, the Dow Jones 30 industrials composite index realizes a loss? Specifically, find P(%FSDJ < 0).

ANSWER:

To formally test for normally distributed returns; we examine two parameters that characterize a normal distribution. The first parameter is SKEWNESS, which measures the symmetry in a distribution and is defined as the normalized third moment of a distribution. For distributions that are normally distributed, the skewness parameter is zero. Accordingly, we can test our returns data for normality by testing the null that are returns data have a skewness parameter of zero.

Question #4: Report the estimated skewness parameter. Test the null hypothesis, at the approximate 95% level of confidence, that the skewness of our returns data is zero using the result that the sample skewness parameter estimator is normally distributed with mean 0 and variance 6/T, where T is the sample size.

ANSWER:

Another parameter used to define a normal distribution is KURTOSIS, or the normalized fourth moment, which characterizes the "peakedness" of a probability distribution. The normal distribution has kurtosis equal to 3, but fat-tailed distributions with extra probability mass in the tail areas have higher kurtosis. Accordingly, we can test our returns data for normality by testing the null that returns have a kurtosis parameter of 3, i.e., reject in favor of excess kurtosis.

Question #5: Report the estimated kurtosis parameter. Test the null hypothesis, at the approximate 95% level of confidence, that the kurtosis of our returns data is 3. Employ the result that the sample kurtosis parameter estimator is normally distributed with mean 3 and variance 24/T, where T is the sample size.

ANSWER:

Question #6: What do our skewness and kurtosis test results imply about the distribution of daily returns on the Dow 30 over the period 1980M1-1997M4?

ANSWER:

Student Programming Questions

Question #1: What does the finding of excess kurtosis imply about our results in Question #3 above?

Question #2: Explore alternative ways to plot our return data. Which graph best represents the relative frequency of the return data?

Question #3: Try redoing the case with a different sample period or a different portfolio of stocks and assess the "robustness" of the results presented in this case.