Goal: This case introduces the statistical testing of some important fundamental economic relationships frequently used in structural economic forecasting models. Specifically, it introduces how to:

• Produce Correlation Statistics using FORECASTX^TM
• Estimate some Fundamental Macroeconomic relationships
• Perform Hypothesis Tests on Population Correlation Coefficients.

The spreadsheet for this problem is CH2_Case2.xls.

Sheet One contains the following data used in Part 1 of this assignment:

The series MONEY_STOCK is the M2 measure of the money supply. The M2 money supply measure includes liquid short-term securities such as money market funds and small time deposits as well as cash and deposits.

The series PRICE_LEVEL is the consumer price index, non-seasonally adjusted.

The series %MS is the percentage change in the MONEY_STOCK.

The series %CPI is the percentage change in PRICE_LEVEL, i.e., the rate of inflation.

Sheet Two contains the following data used in Part 2 of this assignment:

The series BUDGET is the official federal budget surplus (deficit) in billions of dollars, non-seasonally adjusted.

The series RATE is the conventional fixed-rate mortgage interest rate percent-per annum, non-seasonally adjusted.

The forecaster often uses economic theory in building what are called "causal" or structural forecasting models, notably regression analysis. Here we will examine two widely held economic relationships that relate to forecasting inflation and interest rates.

Relationship #1: Inflation is primarily a monetary phenomenon. This view takes a long-term perspective and argues that excessive monetary growth causes inflation, defined as the percentage rate of change of the overall level of prices. Accordingly, factors such as wage increases and supply shocks only cause one-time price increases and are not correctly interpreted as causing inflation.

Relationship #2: Large Federal budget deficits lead to higher interest rates. This view argues that there is a fixed pool of savings to fund both public and private sector overspending. Therefore, as the public sector's demand for those funds is driven up due to large deficits, the cost of borrowing, i.e., the interest rate will increase crowding-out marginal borrowers. Accordingly, there should be a positive relationship between budget deficits and long-term interest rates.

We can examine these relationships by producing scatter-plots and estimating correlation coefficients using FORECASTX^TM.

Using the FORECASTX^TM, we estimated the following correlation coefficients between the MONEY_STOCK and PRICE_LEVEL over the sample period.

Clearly, the level of the money stock is highly positively correlated with the level of the CPI index. Indeed, the estimated correlation coefficient of .98 is very close to the limiting value of one. However, the data are in level form, not proportionate changes, which the theory implies since we are ultimately concerned about inflation (defined as the rate of change of the price level).

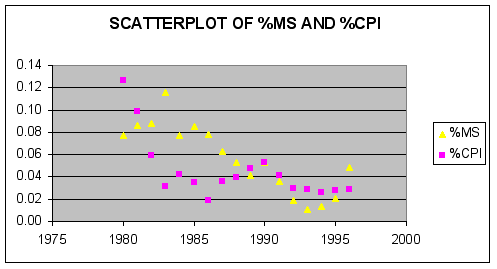
Using Excel, a scatterplot of %M2 and %CPI is shown below.

Note how the size of the correlation coefficient has changed dramatically when the data are transformed into proportionate changes. This is common in financial data, i.e., prices are highly correlated, but price changes are quite random and uncorrelated.

Question # 1: Based upon examination of the scatter plot and estimated correlation coefficient between the percentage change money supply (%MS) and rate of inflation (%CPI), does the data support the hypothesis that excessive monetary growth causes inflation? Specifically, test the null hypothesis that %M2 and %CPI are uncorrelated at the 5% level of significance using a one-tailed test.

ANSWER:

Using FORECASTX^TM we obtained the following estimates of the correlation between deficits and long-term mortgage interest rates.

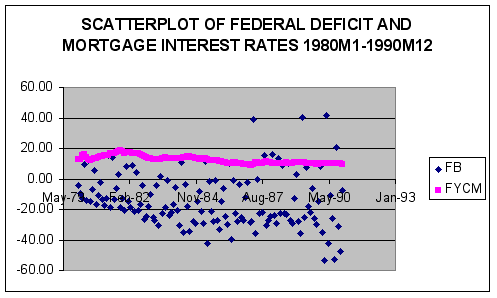
Question # 2: Based upon examination of the scatter plot and estimated correlation coefficient between the long-term fixed mortgage rate and the federal budget surplus (deficit), does the data support the hypothesis that deficits lead to increases in interest rates? Specifically, test the null hypothesis that interest rates and deficits are not positively related at the 5% level of significance using a one-tailed test.

ANSWER: P>

Question #1: Can you explain why the null and alternative hypotheses were formulated is this case? Why were one-tailed t-tests used instead of two-tailed tests?

Question #2: Redo the analysis on the relationship between inflation and the rate of change in the M2 money supply using quarterly data over a larger period of time. Contrast and compare your results with Part I of this case.

Question #3: Explain our finding that levels of M2 and the CPI are highly correlated, but percentage changes are not. Which measure is the "true" test of inflation models?

Question #4: Explain what is meant by "normalized covariance."