CSE 40/60657: Natural Language Processing
Homework 0
- Due
- 2014/01/22 at 11:59 pm
- Points
- 0
This homework will not be graded, but the instructor will be happy to discuss it with you. Its purpose is to help you decide whether you have the right background to take the class. These questions should be easy for you – especially question #1.
-
Write a program that reads in a text file, splits on whitespace to form a sequence of words, and outputs the 10 most frequent words. Show solution
import fileinput, collections, heapq, operator n = 10 count = collections.Counter() for line in fileinput.input(): words = line.split() for word in words: count[word] += 1 largest = heapq.nlargest(n, count.iteritems(), operator.itemgetter(1)) for word, count in largest: print word -
Write a finite-state automaton that generates strings over $\{a,b\}$ that have exactly five $a$’s and five $b$’s, in any order. Show solution
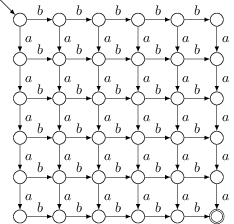
-
Describe an algorithm (or write a program) that uses dynamic programming to count how many such strings there are. Hint: it is row 10, column 5 (using zero-based indexing) of Pascal’s triangle. Show solution
na = nb = 5 count = [[0 for ib in xrange(nb+1)] for ia in xrange(na+1)] for ia in xrange(na+1): for ib in xrange(nb+1): if ia == ib == 0: # empty string count[ia][ib] = 1 if ia > 0: # add a count[ia][ib] += count[ia-1][ib] if ib > 0: # add b count[ia][ib] += count[ia][ib-1] print count[na][nb] -
Suppose that 1/100,000 of the population has ESP. You have a test for ESP that, if someone has ESP, reads positive with 95% probability; and, if someone doesn’t have ESP, reads negative with 99.5% probability. I take the test and it reads positive. What’s the probability that I have ESP? Show solution
$$\begin{align} P(\text{ESP}) &= 0.00001 & P(\neg \text{ESP}) &= 0.99999 \\ P(\text{positive}\mid\text{ESP}) &= 0.95 & P(\neg \text{positive}\mid\text{ESP}) &= 0.05 \\ P(\text{positive}\mid\neg \text{ESP}) &= 0.005 & P(\neg \text{positive}\mid\neg \text{ESP}) &= 0.995 \end{align}$$ $$\begin{align} P(\text{ESP} \mid \text{positive}) &= \frac{P(\text{ESP}, \text{positive})}{P(\text{ESP}, \text{positive}) + P(\neg \text{ESP},\text{positive})} \\ &= \frac{0.95 \times 0.00001}{0.95 \times 0.00001 + 0.99999 \times 0.005} \\ &\approx 0.0019. \end{align}$$
-
If $\mathbf{w}$ is a vector with components $w_i$, then
$$\frac{\partial}{\partial w_i} \ln \frac{1}{1 + e^{-\mathbf{w} \cdot \mathbf{x}}} = \mathord{?}$$
Show solution
$$\begin{align} \frac{\partial}{\partial w_i} \ln \frac{1}{1 + e^{-\mathbf{w} \cdot \mathbf{x}}} &= - \frac{\partial}{\partial w_i} \ln (1 + e^{-\mathbf{w} \cdot \mathbf{x}}) \\ &= - \frac{x_i}{1+e^{-\mathbf{w} \cdot \mathbf{x}}}. \end{align}$$