GAME THEORY and Prisoner's Dilemma
[I am working on the graphics...]
Professor Dan Lindley
448 Decio, 631-3226, dlindley@nd.edu
August 12, 1999, Rev. 1.4
Prisoner's Dilemma is the most commonly used form of game theory in security studies. Game theory (PD) is an analytical tool and abstraction that can be used to increase understanding of both the arms race and the geo-politics of the cold war.
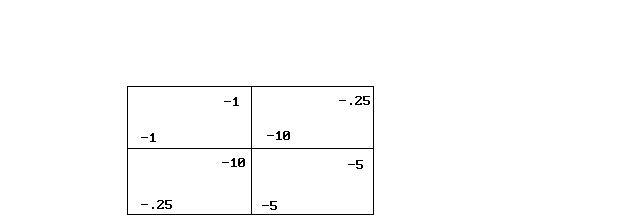
In PD, two thieves are caught by the police but, due to lack of evidence, neither can be convicted without the implicating confession of the other. The prosecutor separates the prisoners so that they ca not communicate and tells each: if both of you remain silent, you will be prosecuted on a minor charge and get 1 year in prison. If you both confess, you each get 5 years. If one confesses and the other does not, the confessor gets a very light sentence (.25) while the other gets 10 years. The choices and the resultant outcomes (payoffs) can be depicted in a two by two matrix:
Prisoner # 1
Silent Confess

Silent
#2
Confess
(Example of how to read the 2x2 matrix: in the lower left box, prisoner #2 receives almost no time in prison while prisoner #1 gets 10 years.)
Unable to communicate and knowing each other to be as trustworthy as thieves tend to be, they each confess and both end up in the lower right box.
How does this relate to national security? In place of the prisoners, the interactions of two adversaries can be substituted in the matrix, illustrating several characteristics of arms races and geo-politics.
Arms races and geo-politics are often viewed as zero-sum games. Zero-sum means that when one side gains (an amount of something), the other loses (an equal amount). Thus, zero-sum games result in relative gains or losses. The word 'relative' indicates that each player's position is measured 'relative' to the other. Zero-sum games usually imply that players are fighting over a fixed and finite amount of something: area on a chessboard, amounts of wealth, allies, etc.
If both players are able to make simultaneous gains, then it is a positive-sum game. Competition is often viewed as a zero-sum game, while cooperation is usually undertaken to achieve positive-sum results. When players are concerned over relative position (my position as measured by your position), this can aggravate tensions more than when they are concerned over 'absolute' position (my position, regardless of your position). Think about it.
When the world was divided into opposing U.S. and Soviet 'camps' during the cold war, a shift of camp by a minor country was a relative shift in the superpower balance: one camp gained and the other lost. This would have also been true in the arms race if one side had gained a decisive lead in some form of decisive weaponry.
However, this rarely happened. Instead, the arms race caused greater and greater insecurity for both sides (you may disagree here - would not larger arsenals also make deterrence more robust? What about crisis stability?). As arsenals grew, the amount of damage war could cause increased and large sums of money and talent continued to be spent. The superpowers went down this road together and their levels of security dropped in a negative-sum game.
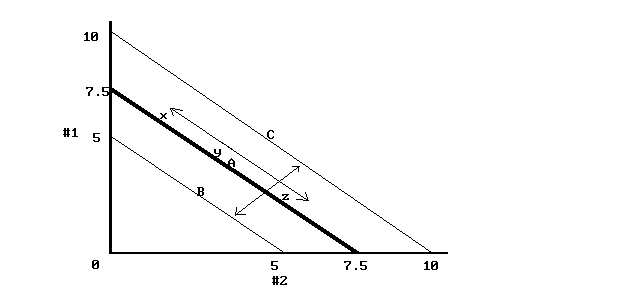
This graph shows the difference between zero and positive/negative sum games. When relative position shifts, as in a zero-sum game, it is reflected along a single line. This is seen at points x, y, z along line A below. Along line A, the aggregate total of whatever one is measuring along the axes (area, wealth, etc) remains the same no matter where one is located. However, the share allocated to #1 and #2 shifts. When absolute position shifts, as in a positive/negative sum game, that is reflected in moving from line A to line B or C. The aggregate total shifts but the share does not.
It is worth noting that absolute and relative shifts can occur simultaneously or in sequence. For example, the security dilemma (as discussed in class) is typically a two-part sequence. Player 1 tries to achieve the upper right box (new weapon). Player 2 counters this (builds same weapon) and in doing so, both move into the lower right box.
The outcomes for each side depend on actions by the other. The two payoffs for each player are interdependent. Whether or not Player 1 gets to achieve or remain in the upper right box depends on what the other does. This seems to be an obvious point, but this interdependence is at the heart of the security dilemma. The security dilemma has been ignored by nations time and again throughout history.
**************** ADDITIONAL COMMENTS ********************
The outcomes in PD can vary due to a wide variety of factors; the preferences (the codes in each box) are not fixed. What are the players' (subjective) preferences? How well do the players know each other? Has their past behavior created any predictable patterns? Can the players communicate? Even if the player's have no means of communication, what happens if they play over and over again? Can a history of repeated play serve as a form of communication? How can the players alter the payoff matrix and try to obtain various outcomes? How can an outside force alter the payoff matrix? To what extent does this whole framework depend on rationality?(1) How do the boxes change if seen through each of Allison's models? What would you put in the boxes to represent the nuclear arms competition between India and Pakistan, in the Korean peninsula...?
Free Thought Zone:
Player ?
No X Yes X

No X
Player ?
Yes X
1. For more on these brain-busters, see Kenneth Oye, "Explaining Cooperation under Anarchy: Hypotheses and Strategies," in Kenneth Oye, ed., Cooperation Under Anarchy (Princeton, NJ.: Princeton University Press, 1986). Each of these sentences is the subject of several paragraphs.