





The objectives for this assignment are for you to:
mkdir cse20211/lab5 cd cse20211/lab5For this assignment, you will be using the simple graphics library created for this class. Follow that link, download the example program, and skim through the function reference. (Return to it later as needed.)
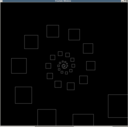
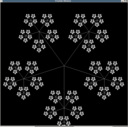
Each fractal shape should be drawn by a recursive function that stops recursing when the scale of drawing becomes too small. Your display may differ from the examples slightly, as long as the topology is clearly the same. For example, your tree should branch into two at each point, but need not be exactly the same height and width. You may need to peer at the image for a little while before you decode what is going on. (Click each for a bigger image.)
| 1 - Sierpinski Triangle | 2 - Shrinking Squares | 3 - Spiral Squares | 4 - Circular Lace |

| 
| 
| 
|
| 5 - Snowflake | 6 - Tree | 7 - Fern | 8 - Spiral of Spirals |

| 
| 
| 
|
Note: completing the first two fractals is sufficient to earn a participation point for the lab.
There is one tricky requirement: Your program must contain only ONE recursive function. The function should have appropriate parameters to control the color, branching factor, size, etc. By calling the function multiple times with different parameters, you should be able to create significant variations in the shapes actually drawn.
Some ideas to get you thinking:
A fractal is most easily drawn on a computer by a recursive function. Any kind of recursive function must have a base case which terminates the recursion, and a recursive case which draws one piece of the figure, and then calls the function again (possibly several times) with slightly different arguments.
Let's start by working out fractal #1, the Sierpinski Triangle.
First, identify the basic shape of the fractal, and write a bit of code to draw it. The basic shape for #1 is the triangle, so write a function to draw that:
void draw_triangle( int x1, int y1, int x2, int y2, int x3, int y3 )
{
gfx_line(x1,y1,x2,y2);
gfx_line(x2,y2,x3,y3);
gfx_line(x3,y3,x1,y1);
}
Now, let's work on the recursive function, which usually has parameters similar to
that of the basic shape. Write out the function body for fractal_triangle,
It should have a base case, a drawing step, and a recursive step.
The drawing step is easy, so add that first:
void fractal_triangle( int x1, int y1, int x2, int y2, int x3, int y3 )
{
/* Base case will go here. */
/* Drawing step. */
draw_triangle(x1,y1,x2,y2,x3,y3);
/* Recursive step will go here. */
}
Next, determine the recursive step. Each large triangle will consist of several small triangles, so call fractal_triangle recursively to create the smaller triangles:
void fractal_triangle( int x1, int y1, int x2, int y2, int x3, int y3 )
{
/* Base case will go here. */
/* Drawing step. */
draw_triangle(x1,y1,x2,y2,x3,y3);
/* Recursive step. */
fractal_triangle(x1,y1, (x1+x2)/2, (y1+y2)/2, (x1+x3)/2, (y1+y3)/2 );
fractal_triangle( /* coords of small triangle 2 */ );
fractal_triangle( /* coords of small triangle 3 */ );
}
The example above will compile and run, but it will recurse forever and eventually crash the program. (Try it if you like.) Every recursive function must have a base case to stop the recursion, so let's stop when the triangles get small:
void fractal_triangle( int x1, int y1, int x2, int y2, int x3, int y3 )
{
/* Base case. */
if( abs(x2-x1) < 5 ) return;
/* Drawing step. */
draw_triangle(x1,y1,x2,y2,x3,y3);
/* Recursive step. */
fractal_triangle(x1,y1, (x2+x3)/2, (y2+y3)/2, (x1+x3)/2, (y1+y3)/2 );
fractal_triangle( /* coords of small triangle 2 */ );
fractal_triangle( /* coords of small triangle 3 */ );
}
To sum up, here is a checklist for a good recursive fractal function:
Turn in fractals.c, gallery.c, and report.txt. Your lab report should explain the final part of the assignment, explaning how it works from the user perspective, how the program works internally, and how you verified that the output of the program is correct.
Please review the general instructions for turning in.