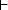 p
p
Frege’s first fundamental distinction is between, as people now put it, the content of a sentence and an attitude that someone might take to that sentence. He discusses this distinction as it applies to the case of a particular attitude: that of judgement. But the point is a general one. We can distinguish between:
The judgement that grass is green.
The assertion that grass is green.
The supposition that grass is green.
The denial that grass is green.
which are all different attitudes that one can have to the content of the sentence, ‘Grass is green.’ We can signify that content, apart from any attitude towards it, as Frege suggests by means of the phrase ‘the proposition that grass is green.’
How this distinction separates Frege from many traditional discussions of logic, which are couched in terms of ‘assertions’ or ‘judgements’ rather than talk of propositions. The philosophical importance of the distinction. (For an influential and important discussion of the relevance of the distinction, see Geach’s “Assertion”, in Philosophical Review (1965).)
Frege further distinguishes between two different kinds of contents: those that can, and those that cannot, be the content of a judgement.
In Frege’s symbolism, if we represent a proposition with a letter, like ‘p’, we would represent the judgement that p using the ‘judgement-stroke’ as follows:
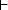 p
p
If we just wanted to represent the fact that p is a ‘judgeable’ content, without talking about any particular judgement that p is the case, we could use Frege’s ‘content-stroke’, as in
-p
Although Frege’s distinction between content and attitude has been enormously influential, his judgement- and content-strokes have not entered into the vocabulary of contemporary logic and philosophy of language. This is partly because, having absorbed Frege’s lesson, we now simply talk about propositions by using variables to stand for them, without having to use the content- and judgement-stroke to disambiguate between talk about the content and talk about a judgement with that content. Now, whenever one wants to talk about, e.g., the judgement that grass is green rather than simply about the proposition that grass is green, it is expected that this is made explicit by using the term ‘judgement’ (or ‘assertion, or ‘belief’, or whatever attitude towards propositions one wants to discuss).
One reason why Frege’s distinction here is influential is that it separates questions about the meanings (contents) of various expressions from questions about what it is to make a judgement, assertion, etc. using those expressions. This is something to which we will return later in the course.
We will be skipping this discussion for now. We will pause only to explain two aspects of Frege’s symbolism in terms of the more familia notation of contemporary logic:
The material conditional:
Informally: If p then q
Standard notation: p  q
q
Frege notation: ___ q p
Negation:
Informally: Not p
Standard notation: ¬p
Frege notation: ___ p
(We will postpone our discussion of this section until we discuss Frege’s later article, “On Sense and Reference.”)
To understand why Frege’s analysis of language was revolutionary, it is useful to have some grasp of the subject/predicate analysis of language which it overthrew; the easiest way to approach this is via Aristotle’s theory of the syllogism.
It is worth pausing at this point to ask about the relationship between (deductive) logic and the philosophy of language.
One of the tasks of the philosophy of language is to explain the relations between linguistic expressions and the world in virtue of which certain sentences are true or false. Now, it seems plausible that any account of what makes certain sentences true or false will be given in terms of the connections between various sub-sentential expressions and objects and properties in the world. The fact that, e.g.,
Grass is green.
is true evidently has something to do with the fact that ‘grass’ is a word for certain plants found frequently in front yards and that ‘green’ is a word for a particular color. This indicates that any complete philosophy of language will have to provide some sort of analysis of sentences into their parts which can explain how the conditions which would make those sentences true are determined by those parts.
But what does this have to do with logic? Deductive logic is the study of the truth-involving relations between sentences; logicians are especially interested in giving a general answer to the question: When does the truth of one set of sentences guarantee the truth of some other sentence? (I.e.: What does it take for one sentence to follow from another?) It’s clear that giving a general answer to this question will also involve giving some kind of analysis of sentences into their parts, since whether one sentence follows from another is typically a matter of relations between parts of those sentences.
The important point to note is that the two kinds of analyses of sentences are likely to coincide. The latter kind of analysis is meant to explain the truth-involving relations between sentences. The most natural way to pursue this kind of analysis would be to explain the structural features of sentences in virtue of which they have certain truth conditions, and then to explain logical consequence in terms of these features. But, if this is so, then the most natural way to give a theory of logical consequence for a language will also give us the kind of structural explanation of language-world relations which we are looking for in the philosophy of language.
The moral of all this, for our purposes, is that a theory of logical consequence typically involves a theory of the structural features in virtue of which sentences have certain truth conditions. So, if we are out to provide a theory of the latter type, we can look at logic for some possibilities and tests of adequacy.
Accordingly, to see what kind of analysis of language prevailed throughout most of Western philosophy, it makes sense to look at the logical system which prevailed throughout most of Western philosophy: Aristotle’s theory of the syllogism. Aristotle’s Prior Analytics is devoted to explaining the nature of demonstration; he introduces the topic by saying
“We must ...define a premiss, a term, and a syllogism ...and after that, the inclusion or non-inclusion of one term in another as in a whole, and what we mean by predicating one term of all, or none, of another.” (24a10-15)
Premises are sentences which, Aristotle says, will be
“an affirmation or denial of something concerning something else.” (24a26-27)
He goes on to distinguish three different ways in which something may be said of something else (modes of attribution): universal, particular, and indefinite (25a2-5). When he goes on to discuss demonstration and to give an account of what we might call the types of valid argument, he does so in terms of this catalogue of distinctions between types of sentences. The following syllogism is an example:
| Major premise. | All mammals are animals. |
| Minor premise. | All dogs are mammals. |
| Conclusion. | All dogs are animals. |
This is the ‘first figure’ of the syllogism, in which the subject of the major premise is the predicate of the minor premise, the predicates of the major premise and the conclusion are the same, and the subjects of the minor premise and the conclusion are the same. Each of the premises and the conclusion of this instance of the first figure are both universal predications (as opposed to particular or indefinite ones) and are affirmations (as opposed to negations/denials). The first figure, with all sentences universal and affirmative, is valid. (Some changes would make it invalid, as if the major premise were particular rather than universal. Other changes would preserve its validity, as if the minor premise and conclusion were both particular rather than universal.)
The central point to notice: the most general distinctions between classes of sentences are distinctions between modes of predication. What this seems to presuppose about the general (subject/predicate) forms of sentences. Consequences of this for logic, and the philosophy of language.
Frege suggests that the Aristotelian subject/predicate analysis of sentences goes wrong by following the superficial appearance of natural language too closely. He gives the following argument for this claim:
“A distinction of subject and predicate finds no place in my way of representing a judgement. In order to justify this, let me observe that there are two ways in which the content of two judgements may differ; it may, or may not, be the case that all inferences that can be drawn from the first judgement when combined with certain other ones can also be drawn from the second when combined with the same other judgements. The two propositions ‘the Greeks defeated the Persians at Plataea’ and ‘the Persians were defeated by the Greeks at Plataea’ differ in the former way; even if a slight difference of sense is discernible, the agreement in sense is preponderant. Now I call the part of the content that is the same in both the conceptual content. Only this has significance for our symbolic language ...” (§3)
Frege’s point here is that the subject/predicate analysis makes distinctions between sentences which do not reflect anything about the logical properties of sentences, or the conditions under which they are true.
How serious is this as a criticism of the subject/predicate analysis of language?
It is one thing for a theory to make too many distinctions; it is a far worse problem if a theory does not have the resources to explain the facts it is out to explain. The problem of multiple generality is an argument that the subject/predicate analysis is incapable of explaining the logical relations of a very large class of sentences.
Sentences of multiple generality are sentences which contain more than one expression of generality, such as ‘someone’ or ‘everything’, like
Everyone loves someone.
The problem of multiple generality is the problem of accounting for the logical relations in which sentences of multiple generality stand. And example of the kind of logical relation which proved problematic for Aristotelian logic and its successors was the fact that
Someone is loved by everyone.
seems to logically entail
Everyone loves at least one person.
How might you try to explain this entailment in terms of Aristotelian logic?
In place of Aristotle’s analysis of sentences into subject and predicate, Frege proposed an analysis of sentences into function and argument(s).
A familiar example of an expression which stands for a function is ‘+.’ This sign stands for a function from pairs of numbers to numbers; i.e., the addition function takes pairs of numbers as its arguments and yields a number as its value. To understand how expressions of natural language might be akin to ‘+’, we should ask a number of questions: (i) Which expressions stand for functions, and which for arguments to those functions? (ii) What kinds of things do these functions have as their arguments and values?
The way Frege introduces the topic in §9, it seems that there is no general answer to (i). He says:
“If an expression is thought of as variable in this way, it is split up into a constant part representing the totality of these relations and a symbol, imagined as replaceable by others, that stands for the object related by the relations. I call one part the function, the other an argument. This distinction has nothing to do with the conceptual content; it concerns only our way of looking at it.”
This seems to indicate that, given some sentence like
Hydrogen is lighter than carbon dioxide.
there is no fact of the matter which of these expressions stand for functions, and which for arguments to those functions. It depends, Frege indicates, which of these expressions we are regarding as variable (replaceable by other expressions), and which we are regarding as constant. Indeed, the number of argument-places in the sentence can also depend on this.
Frege says that there is one exception to this general rule that the function/argument distinction is not a distinction in conceptual contents, but only in our way of looking at them:
“We attach no importance to the various ways that the same conceptual content may be regarded as a function of this or that argument, so long as function and argument are completely determinate. But if the argument becomes indeterminate, ...then the distinction between function and argument becomes significant as regards the content. Conversely, the argument may be determinate and the function indeterminate. In both cases, in view of the contrast determinate-indeterminate ...the whole proposition splits up into function and argument as regards its own content, not just as regards our way of looking at it.”
What Frege means by ‘indeterminate’ here.
There is a tension in Frege’s discussion here. First, he says that in standard cases there is no intrinsic distinction between argument-expressions and function-expressions. Second, he says that when either a function or argument is indeterminate, there is an intrinsic distinction between function and argument. But this is puzzling. We have two different cases of indeterminacy: one in which a function is indeterminate, and one in which an argument is indeterminate. But what determines whether a given instance of indeterminacy falls into the first or the second of these categories? It can’t, on Frege’s view, be whether the place in the sentence where the indeterminacy occurs is an argument-place or a function-place; for we have already seen that he thinks that there is no objective distinction here. But surely there must be some systematic explanation.
This tension in Frege’s discussion in §9 can be resolved by treating the distinction between functional expressions and argument-expressions as an objective one, which is independent of the way we might happen to divide up the sentence, or think of parts of it as variable, on a given occasion. And, indeed, this is the way that Frege seems to treat the distinction in §10.
A possible explanation of the tension: the distinctions between argument and function, and between variable and constant.
Other reasons why this is desirable; the role of the distinction between function and argument in explaining logical consequence.
The function/argument analysis as solving our first two problems with the subject/predicate analysis of sentences.
So far, however, we have not answered either of our questions (i) and (ii). (What are the functional expressions? What do the relevant functions have as their arguments and values?)
We can make some progress towards answering these questions, and to seeing how Frege’s analysis might be able to solve the problem of multiple generality, by looking at Frege’s treatment of sentences containing devices of generality.
At the outset of §11, Frege suggests an addition to his notation: an concavity in the content-stroke, in which is placed a Gothic letter. Frege explains its significance as follows:
“In the expression for a judgement, the complex symbol to the right of __ may always be regarded as a function of one of the symbols that occur in it. Let us replace this argument with a Gothic letter, and insert a concavity over the content-stroke, and make the same Gothic letter stand over the concavity: e.g.:
__ a__
a__ 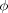 (a)
(a)
This signifies that the function is a fact whatever we take its argument to be. ...From such a judgement, therefore, we can always deduce any number we like of judgements with less general content, by substituting something different each time for the Gothic letter; when this is done, the concavity in the content-stroke vanishes again.”
This is Frege’s first informal explication of universal quantification. By the formula
___ a__
a__ 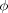 (a)
(a)
Frege means what we would express by saying
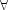 x
x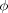 (x)
(x)
Here Frege gives, in effect, a statement of the rule of universal instantiation, that from any universally quantified formula
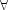 xF(x)
xF(x)
we can infer, for any object a,
Fa
This marks the beginning of a fundamentally new treatment of generality. On the subject/predicate analysis of language, both the sentences
Everything is F.
a is F.
are, whatever the differences between them might be, of the same logical form. Frege is suggesting that these sentences are of fundamentally different forms.
Using universal quantification and negation, Frege is also in a position to express existential quantification. What we would write as
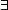 xFx
xFx
Frege can express in his notation as
______ x__ ____ Fx
x__ ____ Fx
See §12 for Frege’s discussion of this.
(Given that the notations are inter-translatable, we will from now on use the more familiar and less cumbersome modern notation.)
Consider how this might help with the problem of multiple generality, specifically with the problem of explaining the validity of the inference from
Someone is loved by everyone.
to
Everyone loves at least one person.
What are the logical forms of these sentences? We might formalize this inference as:
|
|
|
|
How the introduction of quantifiers breaks down the distinction between subject and predicate.
Unanswered questions (the same as (i) and (ii) from above): Which expressions are function-expressions and which argument-expressions? What do the relevant functions have as their arguments and values?