Power

Now consider a small amount of charge $\Delta q$ that is entering a device. Assume that the voltage across the device is $v$. The work done in this case will be

$$\Delta w = v \Delta q$$

If this work is done over the time interval $\Delta t$, then the average rate at which work was done (assuming $v$ is constant) is given by the equation

$$\frac{\Delta w}{\Delta t} = v \frac{\Delta q}{\Delta t}$$

As $\Delta t \rightarrow 0$, we see that the instantaneous power of the device is

$$\mbox{instantaneous power} = \lim_{\Delta t \rightarrow 0} \frac{\Delta w}{\Delta t} = \lim_{\Delta t \rightarrow 0} v \frac{\Delta q}{\Delta t} = v \frac{dq}{dt} = vi$$

The preceding equations imply that the instantaneous power (denoted as $p(t)$) delivered at time $t$ to a device with current $i(t)$ and voltage $v(t)$ is

$$p(t) = i(t) v(t)$$

This power is measured in watts (J/sec).

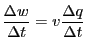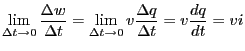Note that power also has a sign. If power has a positive sign, then we say that power is absorbed by the system. If power has a negative sign, then the power is delivered by the system. Consider the labelled circuit elements shown in figure 20. The two devices on the right have a power of 10 Watts, so these circuit elements are absorbing power. The other two circuit elements on the left hand side of the figure have an instantaneous power of $-10$ watts. So this second circuit has these circuit elements delivering power to the network.

Figure 20: Power Sign Conventions

The total energy delivered by or absorbed by a circuit element is obtained by integrating the system's instantaneous power. In other words, the total energy (work) is

$$w(t) = \int_{-\infty}^t v(\tau) i(\tau) d \tau$$

We say that a circuit element is passive if the total energy delivered is positive. In other words, the circuit element is passive if

$$w(t) = \int_{-\infty}^t v(\tau) i(\tau) d \tau \geq 0$$

Examples of commonly used passive circuit elements are resistors, capacitors, and inductors. The electrical symbols for such devices are shown in figure 21.

Figure 21: Symbols for resistors, capacitors, and inductors

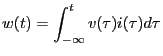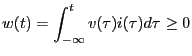Active circuit elements are devices that are not passive. An example of an active circuit element is the independent voltage supply or battery. Another example of an active circuit element is the independent current source. This is a device that can be constructed from transistors. The electrical symbols for these supplies or sources are shown in figure 22

Figure 22: Symbols for Independent voltage supplies and current sources

Remark: What we have discussed up to this point are ideal circuit elements. Note that an ideal circuit element is an abstract mathematical model for the "real thing". These abstractions are useful because they allow us to make quantitative predictions about circuit behavior without having to "build" the real circuit. Such models, however, are obtained by neglecting some real-world aspects of the circuit device. This neglect is justified if what we neglect has a small effect on the overall circuit. Since we are engineers, we usually engineer circuit elements and systems so our ideal analytical model closely approximates the real device. If this "engineering" were not done, then it would be difficult if not impossible to predict circuit behavior prior to building the circuit. Building circuits can be expensive so that the role abstract analysis plays is to provide some guarantees of what we can expect to see once the actual circuit has been constructed.