Nonlinear Control Systems (EE 60580)
University of Notre Dame
Fall 2017 - Enroll in EE60580 section 01
DBRT 208 - TR 12:30-1:45 PM
 |
Nonlinear Control Systems (EE 60580)University of Notre Dame
|
|
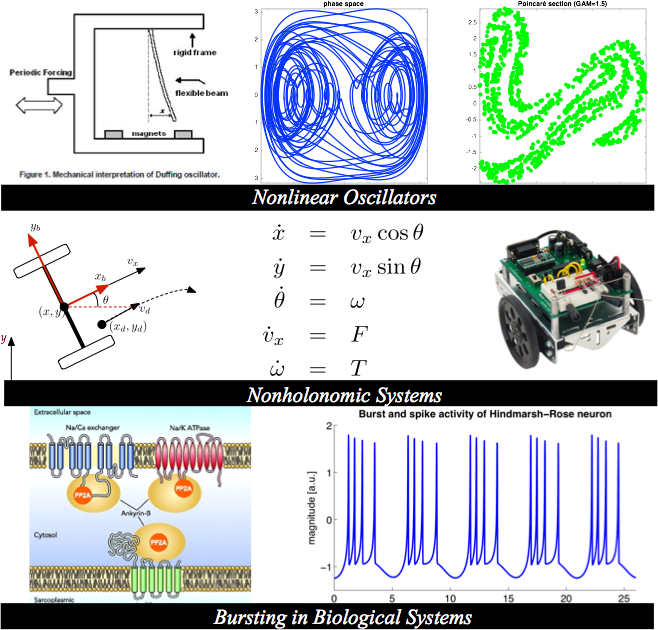
Description: This is a graduate level course in nonlinear control systems that are, primarily, realized as systems of nonlinear ordinary differential equations (ODEs). The course is an in-depth investigation of methods from ordinary differential equations, stability concepts, nonlinear regulators, and the control of bifurcations. The pre-requisites for this course are undergraduate level courses in advanced calculus and ordinary differential equations. An undergraduate level course in signals/systems and a graduate level course in linear systems theory would also be useful. The course will also make use of MATLAB and convex optimization packages (YALMIP/SDPT3). |
Topics
|
|
Grading: 30% Homework, 20% Midterm (1), 20% Final Exam Instructor: Michael Lemmon, Dept. of Electrical Engineering, University of Notre Dame, Fitzpatrick 264, lemmon at nd.edu Textbook: Online Lectures Notes (see vault) Reference Textbooks
|