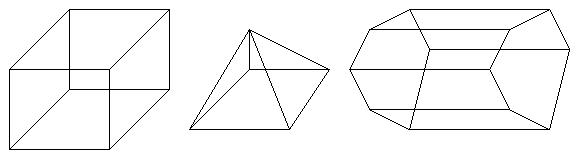
Consider these three-dimensional figures:

If, for each shape, you count the numbers v, e, and f of vertices, edges, and polygons (a.k.a. faces), and compute v - e + f, you get 2 for each one. This is not just a coincidence: each of these shapes can be deformed continuously into each of the others, and in fact into a sphere, and a famous theorem of Euler's says that for any such shape, v-e+f=2.
If, on the other hand, you consider this shape (a brick with a
square hole drilled through it):
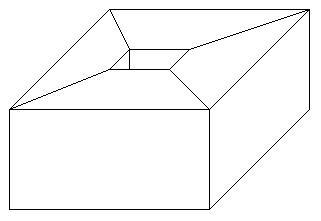
Counting things like vertices, edges, and faces and then considering expressions like v-e+f is part of combinatorial topology, which is the focus of this course.
We will start with Euler's formula, then talk about some fundamental topological ideas like compactness. We will move on to vector fields, the Brouwer fixed point theorem, winding numbers, and the Poincaré index theorem. Next comes the Jordan curve theorem: every simple closed curve in the plane divides the plane into two pieces. This is notorious for being easy to state, ``obviously'' true, but difficult to prove. We will also discuss the classification of surfaces, and (time permitting) homology, Betti numbers, Euler's formula revisited, and the Poincaré index theorem revisited.
PREREQUISITES: The students should have a basic background in advanced calculus, passing familiarity with differential equations, and it wouldn't hurt to know a bit of group theory.
TEXTBOOK: A Combinatorial Introduction to Topology by Michael Henle (the paperback edition of which costs around $10.00, the last time I checked).
Go to John Palmieri's home page.
John H Palmieri