INTERPRETING COMPLEX NONLINEAR MODELS

Lawrence Marsh and Maureen A, McGlynn, University of Notre Dame

Deboparn Chakraborty, University of Wisconsin-Milwaukee

ABSTRACT

This paper demonstrates the use of SAS software in the systematic evaluation and interpretation of complex nonlinear models. This impact of a unit change in one explanatory variable on the dependent variable of a nonlinear model is difficult to determine since the change in the predicted value is conditional on all of the other variables for that observation. Furthermore, attempts to approximate this relationship have proven inadequate and often meaningless. In this paper, we present an alternative approach to evaluating the marginal effects of a unit change in the explanatory variables which uses individual observations to calculate the change in the predicted value brought about by a unit change in one of the explanatory variables to illustrate the variable's distributional impact on the dependent variable. Examples of a CES production function, a logit model and a neural network model are provided to illustrate the application of this technique using SAS software.

INTRODUCTION

The standard nonlinear regression model can be expressed by the general form

where y_i is the endogenous variable, x_i is a 1*N vector of exogenous parameters, b is a vector of unknown parameters and is the error term which is independent and identically distributed with E(_i)=0 and VAR(_i)=²

To estimate the unknown parameters of a nonlinear model, an objective function is specified and the optimal value of b is computed by solving a system of nonlinear equations. If the distribution of the random error term is unknown, then nonlinear least squares is used to estimate b. The least squares technique finds the values of b which minimize the sum of squared deviations.

Minimization is carried out by an iterative procedure since the system of nonlinear equations does not have an explicit solution.

If the distribution of the disturbance is known, then is estimated using a maximum likelihood approach, where ï the likelihood function is based on the joint probability density of the sample.

For example, if we can assume that

e ~ N(0, )

then the likelihood function may be expressed as

which estimated b and o for b' and 0' and are chosen such that

for all possible and if is unknown.

Despite the fact that complex nonlinear models are becoming more common in economic analysis as well as in other disciplines, their results can easily be misinterpreted. Two common problems associated with complex nonlinear models are the identification of parameters and the interpretation of these parameters in terms of the response of the dependent variable to particular explanatory variables. The problem of identifying specific parameters becomes irrelevant in the context of universal approximators since many alternative universal approximators with different parameter specifications are shown to converge asymptotically to the appropriate generating function. This makes the identification of individual parameters inconsequential. However, the determination and interpretation of the derivative of the dependent variables with respect to each of the explanatory variables requires further analysis.

INTERPRETING COMPLEX NONLINEAR MODELS

In the case of simple linear regression, the interpretation of estimated parameters is straightforward. The linear regression model, which assumes the functional form,
y = X+,

produces estimates of which are easily interpreted as

In other words, the parameter estimates of the linear regression model are the partial derivatives of the dependent variables with respect to each of the independent variables and can be interpreted as the marginal impact of a unit change in as independent variable on the dependent variable.

However, when dealing with a nonlinear model of the functional form

the interpretation of the coefficients is not as straightforward because the derivative of with respect to x varies with the values of x. That is,

which implies that the estimated parameters do not represent the marginal effects of a change in x on y.

The most common method used to determine the impact of a unit change in one of the explanatory variables on the dependent variable is to approximate the relationship by evaluating

However, such attempts at approximation may creates an artificial and often meaningless interpretation. First of all, the mean of the sample may not represent any particular individual or group in the data and may therefore produce misleading implications for policy analysis. For example, if we are interested in the impact of an additional year of education on the wage rate, it may be the case that an additional year of education may have little impact on the wage rates of five sixths of the population but may have ï large impact on the remaining one sixth. Although the average impact may seem significant. it may be insignificant for a large portion of the population and be of importance to only a small group. This distributional impact is not captured by the traditional methods and therefore does not always provide adequate information about the sample.

Secondly. in the case of models which use discrete or dummy variables as explanatory variables, partial derivatives can only be interpreted as Dirac derivatives. Therefore, an alternative approach is necessary.

AN ALTERNATIVE APPROACH

An alternative approach in the interpretation on nonlinear models uses each individual observation and calculates the changes in the predicted value of the dependent variables

brought about by a unit change in the explanatory variable of interest. For linear models, the change in the predicted value would be equal for all observations, but for a nonlinear model, the change in the predicted value is conditional on all other variables for that observation. Therefore, the impact that each explanatory variable has on the dependent variable differs from observation to observation. The subsequent changes in the predicted value brought about by a change in one of the explanatory variables for all observations may be sorted in ascending order

and then plotted to demonstrate the distributional impact of that explanatory variable on the predicted value of the dependent variable.

The remainder of this paper demonstrates this new approach using SAS software for a logistic model of cancer remission, the CES production function, and a neural network model for a nonlinear production function.

Example: Logit Model of Cancer Remission

Lee(1974) estimated the probability of remission in cancer patients based on a set of relevant patient characteristics. We have replicated Lee'e experiment to illustrate how a change in each of the characteristic variables may affect the probability of cancer remission. We begin by estimating the predicted probabilities of the logit model which are of the form

by using the PROC LOGISTIC command in SAS and storing the estimated coefficients and predicted probabilities into a new data file. Each characteristic variable is then increased by one unit while simultaneously holding all other characteristic variables constant at their observed values and the new predicted probability for each observation is calculated. The impact on the dependent variable brought about by each unit change is equal to the difference between the new predicted probabilities (PSTAR) and the original predicted probabilities (PROB), which were generated by the LOGISTIC procedure. The following SAS statements are used to compute the distributional impact on the dependent variable.

ARRAY VARIABLE CELL SMEAR INFIL LI BLAST TEMP;

ARRAY LOGSTAR LOGSTAR1-LOGSTAR6;

ARRAY PSTAR PSTAR1-PSTAR6; correspondents to the number of explanatory variables;

ARRAY PDIFF PDIFF1-PDIFF6;

represents the impact of an independent unit change in each of the explanatory variables on the probability of cancer remission;

ARRAY POUSONE CELL SMEAR INFIL LI BLAST TEMP;

DO OVER PLUSONE;

DO OVER PSI'AR;

PLUSONE=I+VARIABLE;

LOGSTAR=BO+B1*CELL+B2*SMEAR+

B3*INFIL+B4*LI+B5*BLAST+B68TEMP;

PSTAR=(EXP(LOGSTAR))/(1+EXP(LOGSTAR));

PDIFF=PSTAR-PROB;

PLUSONE=VARIABLE-1;

END;

END;

The PDIFFs. which represent

.......... may then be sorted in ascending order and plotted using SAS/GRAPG. Figures 1 and 2 illustrate the impact of a unit increase in CELL and TEMP respectively. In both of these graphs, we see that there is a substantial impact on most of the group. It is also interesting to note that the impact of a unit change in these two explanatory variables on the probability of cancer remission produces a sigmoidal shape, which is characteristic of the logit function, despite the fact that the explanatory variable varies across observations and that the YDIFF variable. This suggests that the shape which the impact variable assumes, which is monotonically by design, is influenced by the structure of the model being estimated.

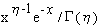
Example 2: CES Production Function

The CES production function to be estimated can be expressed as

The data consists of 309 observations and was taken from Lutkepohl (1980). The PROC NLIN statement, using the Gauss-Newton estimation method, produced the following estimates of b0, b1, b2, and b3:

B₀= 0.124485105

B₁=-0.336341238

B₂= 0.663292542

B₃=-3.010617415

The same SAS procedure used in Example 1 was followed to compute the marginal impact of labor and capital on output, that is,

Figures 3 and 4 show the impact of each factor of production. Both figures show a great degree of disparity across the observations. There was a very small impact on output when capital and labor were marginally increased for a large portion of the sample while a small group experienced a large impact. The next example uses the same production data to estimate the impact of each factor of production on output using a different model specification.

Example 3: Neural Networks and Production

In this example, we use a weighted linear combination of the nonlinear logistic function to estimate a production model using the same data in example 2.

The neural network model to be optimized can be expressed as

where k is the number of nodes in the neural network and a and b are weights which initially define the network.

More specifically, the network used in this example is

Once the model was estimated using the SAS NLIN procedure, we followed the same procedures as in the previous two examples to produce figures 5 and 6. Whereas for the CES production function model the impact of labor and capital on output produced a concave function in which most of the group experienced no impact, the neural network production model shows that a vast majority of the sample experiences some impact when labor and capital are marginally increased.

Despite the fact that the same data set was used in examples 2 and 3, we show that the models produce very different results with respect to the deviates. If the means of the variables were used to evaluated the marginal impacts, that is,

the most likely the results would not have been able to detect a difference in the distributional effects of the CES and neural network models of production.

CONCLUSION

In all three of the examples provided, the results are influenced by the model structure. For the logit model, the impact variable (PDIFF) retained a sigmoidal structure characteristic of the logit model and examples 2 and 3 produced opposite results. This reinforces the idea that the distributional effects of the impact of the explanatory variables on the dependent variable can be of great use in econometric practice. Not only is this approach interesting for policy analysis that attempt to reach a variety of people, especially in issues of social justice, but the results can also offer insight into model design and structure. The fact that the CES and neural network models produced opposite results suggests that perhaps neither of these models represent the appropriate structure for estimating output. Therefore. we may wish to choose a universal approximator to identify specific Parameters. Nonparametric versions of neural network models can sometimes be formulated as universal approximators which have the ability to asymptotically approximate any function and all of its derivatives.