Consider the problem of determining if women are discriminated against in their starting wage. In this example, a person's hourly wage rate will serve as the dependent variable. For simplicity, take months of work experience as the sole explanatory variable. Of course, there are many other variables that might affect a person's wage rate. Moreover, a proper formulation would involve a model derived from economic theory with at least two equations representing labor demand and labor supply, respectively. However, this exposition will ignore these important complications in the interest of clarifying the role of dummy variables in regression and will leave it to others to formulate appropriate models of labor market behavior.
Let yrepresent the iperson's wage rate and xrepresent their
months of work experience in the equation:
yi = b1
+ b2 Xi
+ ei (1)
where bi is the intercept (or starting wage in this example), b2 is the increase in the person's wage for each additional month of work experience, and ei is the error term, with mean zero and variance s2.
For this problem, we focus on the value of b1, which represents the person's starting wage (i.e. when months of experience, Xi , is equal to zero). At this point, we need to create dummy variables to aid us in distinguishing between the starting wage rate for men and the starting wage rate for women.
For men, create a variable, Mi , which is defined to be equal to the value one if the ith person is male and is equal to zero if the ith person is female. Correspondingly, for women, create a variable, Fi , which is one if the ith person is female and zero otherwise. Now introduce Mi and Fi into equation (1) to allow males and females to have their own separate intercepts:
yi = b1
+ b2 Xi
+ b3 Mi
+ b4Fi
+ ei (2)
Unfortunately this equation contains an underidentified set of
parameters (b1,
b3, and b4)
and cannot be estimated without some restriction on the coefficients.
In order to see this point, separate out the men's equation implied
by equation (2) from the women's equation. For the men's equation
Mi is always one and Fi
is always zero, so for men, equation (2) becomes:
yi = (b1
+ b3) + b2
Xi + ei
(3)
Likewise for women, Mi is always zero and Fi is always one, so for women equation (2) becomes:
yi = (b1
+ b4) + b2
Xi + ei
(4)
Unfortunately, although we get estimates of the intercepts (b1
+ b3) and (b1
+ b4), the value
of b1 cannot be
separated from the values of b3
and b4. Some restriction
is needed here to achieve identification of b1,
b3 and b4.
One such restriction is b1 = 0. It makes sense to drop the original intercept term, b1, since men and women already have their own intercept terms, b3 and b4, respectively.
The underidentification of equation (2) can also be expressed
in matrix terms. First, rewrite equation (2) putting the explanatory
variables in a row vector multiplied by the corresponding column
vector of their respective coefficients:
yi = + ei
(5)
Of course, this only represents the ith
observation where i = 1, ..., n. In order to represent the entire
set of n observations at once, we need to "pull the window
shade down" as follows:
= + (6)
This vector-matrix expression may be expressed symbolically as:
y = X b + OE (7)
n x 1 n x 4 4 x 1
n x 1
where y is the n x 1 vector of dependent variable values, X is the n x 4 matrix of explanatory variable values (including a column of ones for the original intercept term), b is the corresponding 4 x 1 vector of regression coefficients, and OE is the n x 1 vector of errors.
Without going into all the mathematics here (see Appendix A for
the details) it can be shown that the sample least squares estimator,
, of the population vector b
is:
= ( X´ X)-1 X´ y (8)
4x1 4xn nx4 4xn nx1
Note that the regular matrix inverse, (X´X)-1, of the X´X matrix only exists as long as there is no exact linear relationship among the columns of the X matrix. If any column of the X matrix can be expressed as an exact linear combination of any of the remaining columns of X, then perfect multicollinearity is said to exist and the determinant of the X´X matrix is equal to zero. This means that the inverse, (X´X)-1 will not exist since calculating the inverse involves a division by the determinant, which, in the case of perfect multicollinearity, means dividing by zero.
It is easy to see that equation (6) presents us with an X matrix
whose first column (the column of ones) is an exact linear combination
of the last two columns (the M and F columns). Since Mi
is always zero when Fi is equal to one and
Mi is always one when Fi
is equal to zero, then it always holds that Mi
+ Fi = 1. Therefore, the first column is
equal to the sum of the last two columns as follows:
= + (9)
Consequently, equation (6) and, therefore, equation (2), presents
us with a case of perfect multicollinearity. This means that
a restriction must be introduced that in effect drops one of these
columns out of the regression. Again, one such restriction is
b1 = 0, which means
dropping the original intercept out of the regression model to
provide the following reduced model:
yi = b2
Xi + b3
Mi + b4
Fi + ei
(10)
In this model, men and women have separate intercepts and no common intercept is necessary.
Now let us return to our original questions: Are women discriminated
against in their starting wage rate? The null hypothesis represents
the case of equal starting wage rates, Ho:
b3 = b4
(equivalently, Ho: b3
- b4 = 0). The
lawyers for Sexism Incorporated would prefer to test this null
hypothesis against the two-sided alternative HA:
b3 ¹
b4 (equivalently,
HA: b3
- b4 ¹
0) because the two-sided approach spreads a given level of significance
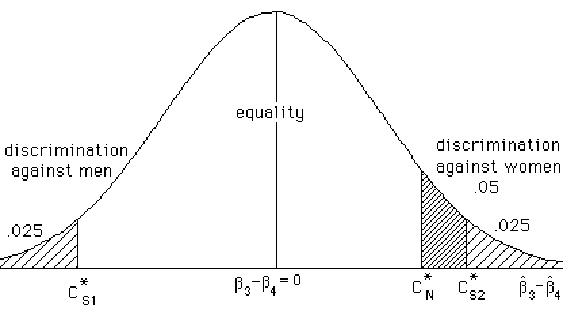
(e.g. a = .05) between the two tails
of the distribution (with a = .025
in each tail). It seems natural to estimate the population difference
in starting wage b3
- b4, with the
corresponding sample difference, 3
- 4. Although the population
difference is viewed (by frequentists and classical statisticians)
as an unknown constant, the sample difference 3
- 4 is a random variable which
serves as our raw score test statistic for this test and may be
normally distributed with a pdf (probability density function),
f(3 - 4),
as depicted in Figure 1. (The Bayesian interpretation will be
given later.)
f(3 - 4)

Figure 1 shows that with a two-tail test using raw score critical points Cand Cthere would be less chance of detecting discrimination against women that with the one-sided test (HA: b3 > b4, or, equivalently HA: b3 - b4 > 0) so the lawyers for NOW will want to use the right-tail critical point, C, instead.
It would be nice to be able to carry out this test in raw score space using 3-4, which is in the original units of measurement of dollars of wage rate differences. However, in order to make use of the distributional tables in the back of your standard statistics textbook, it is necessary to transform the raw score test statistic to standardized form where the transformed (standardized) test statistic will have a mean of zero and a variance of one. Otherwise, authors would have to put an infinite number of tables in the back of their statistics textbook, one for every possible combination of mean and variance. So even though we would prefer to carry out the test in raw score space, we will (temporarily, at least) acquiesce and proceed to transform the raw score test statistic, 3-4, to standardized space, where it will have a mean of zero and variance of one.
In order to carry out the needed transformation we must first determine the distribution of the random variable 3-4. See Appendix B for the details verifying that the difference 3-4 is normally distributed with mean b3 - b4. The variance of 3-4 can be expressed as Var(3-4) = Var3 + Var4 - 2Cov(3, 4). Appendix C shows how to express this variance in terms of the variance-covariance matrix for , Cov() = s2 (X´X)-1.
As always, we must carry out the test as if the null hypothesis were true. The null hypothesis is the straw man that we set up to see if we can knock it down. The null hypothesis is given special protection so that if it is valid it will only be mistakenly rejected one percent of the time (or, in this case, five percent, since we have chosen that to be our level of significance here). Therefore, we give the null hypothesis the benefit of the doubt and follow its specifications so that if we do reject it we will have rejected it on its own terms. That way we cannot be accused of carrying out a test that put the null hypothesis at an unfair advantage. Thus, we stay with the null hypothesis unless we observe an unlikely event under the null hypothesis, that is, a value of the test statistic that falls in the critical (i.e. rejection) region.
Since under our null hypothesis the raw score test statistic
3-4
has a mean of b3 -
b4 = 0 and a variance,
Var(3-4),
we can standardize 3-4
by subtracting the mean (zero) and dividing by the standard deviation
(square root of the variance) to get the standardized test statistic:
Z = ~ N(0,1)
(11)
However, if the variance of the yi, s2,
is unknown, then Var (3-4)
is also unknown and must be estimated by the expression:
Est. Var(3-4)
= Est. Var3 + Est. Var4
- 2 Est. Cov(3,4)
(12)
which uses S2 as an unbiased estimator of
s2 where:
S2 = (y - X)´(y - X)/(n-k). (13)
Since (n-k)S2 / s2
has a chi-square distribution (See Appendix D) and
Est. Var(3-4)
= () Var(3-4)
(14)
= = (15)
which is a student-t distribution with n-k degrees of freedom. Note that a student-t statistic may be defined as the ratio of a N(0,1) random variable divided by the square root of an independent chi-square random variable divided by its degrees of freedom.
The information needed to calculate the
Est.Var(3-4)
= Est.Var3 + Est.Var4
- 2Est.Cov(34) (16)
can be obtained from the Est.Cov() = S2(X´X)-1 matrix.
Most of the major statistical computer packages will allow the user to print out this Est. Cov() matrix. For example, SASì will print out the Est.Cov() matrix if the user specifies COVB as an option on the MODEL statement. The Est.Var(3-4) may be calculated from Est.Cov() matrix as the sum of the (3,3) element plus the (4,4) element minus two times the (3,4) element (or (4,3) element). Of course, the (3,3) element and the (4,4) element may be alternatively obtained by squaring the standard errors printed out (by most statistical packages) next to the estimated regression coefficients, 3 and 4, for Mi and Fi dummy variables.
Given this information the test for the difference between starting
wages is carried out using the above student-t statistic with
n-k degrees of freedom.
A much simpler approach to testing the difference between women's starting wage and men's starting wage can be performed with a somewhat more indirect approach by applying an alternative restriction on equation (2). Specifically, the restriction b4 = 0 results in a quite different interpretation of the b1 and b3 regression coefficients that permits a much easier test of the discrimination hypothesis. The restricted model then becomes:
yi = b1
+ b2Xi
+ b3Mi
+ ei (17)
This can be written in two parts which are implicitly linked together through the intercorrelation of the variables and the pooling of the error term information:
Women's equation (Mi = 0):
yi = b1 + b2Xi + ei (18)
Men's equation (Mi = 1):
yi = (b1
+ b3) + b2Xi
+ ei (19)
These two equations reveal that the wage rate for women with no
experience (Xi=0) is b1
while that for men is b1
+ b3. Consequently,
testing for discrimination against women in this setup merely
involves testing the null hypothesis Ho: b3
= 0 versus the alternative, HA: b3
> 0. This test is easily carried out using any standard
regression program that applies least squares to equation (17).
Again, if the yi (i = 1, ..., n) random variables
are jointly normally distributed, then 3
will be normally distributed since 3
is a linear combination of the yi's (given
that Xi and Mi are nonstochastic).
Under the null hypothesis we have E3
= b3 = 0 so that
our standardized normal test statistic with mean zero (under Ho)
and variance one is:
~ N(0,1) (20)
Next, divide this by which is the square root of a chi-square
random variable over its degrees of freedom. Given that this
chi-square is independent of the standardized normal in (20),
this provides the tstatistic for the b3
coefficient associated with Mi dummy variable
variable with n-3 degrees of freedom (or the F = t2
F-statistic with one numerator degrees of freedom and n-3 denominator
degrees of freedom).
In this section, a regression model with only dummy variables
will be shown to be equivalent to an analysis of variance (ANOVA)
model. This could be extended to control for the influence of
one or more continuous explanatory variables such as years of
experience, Xi, as used in the preceding sections.
Including such continuous control variables in a regression model
along with dummy variables is equivalent to an analysis of covariance
(CANOVA) model. However, this section will focus on the simpler
ANOVA model.
The ANOVA model was developed within the context of formulating an explicit experimental design. In a physics experiment it may be possible to hold temperature constant while varying pressure and then hold pressure constant while varying temperature. Sometimes this is possible in cross-sectional studies in the social sciences as when we hold gender constant as we vary race and hold race constant as we vary gender, and then view the associated changes in hourly wage rate. For the moment we will ignore confounding variables such as years of education or experience that may be correlated with wage rate in a manner that may be unevenly distributed across race and gender. We will deal later with the special methods needed to separate the effects of highly intracorrelated explanatory variables on the dependent variable.
The standard ANOVA model may be expressed as:
yij = m +
aj + eij
(21)
where yij is the hourly wage rate of the ith person in the jth group, m is the grand mean over all individuals, aj is the jth group's deviation from the grand mean and eij is the error for the ith person in the jth group. For our gender discrimination example, the groups are j = M for males and j = F for females. By considering only the effects of gender on hourly wage rate we are restricting ourselves to a one-way ANOVA model. By stating that the aj's are deviations from the grand mean we are implying that those deviations will sum to zero since otherwise the grand mean would not be acting as a true mean for all individuals in the J groups. This means that in our example, aM + aF = 0, and in general, = 0. For the men, the average hourly wage rate is m + aM and for the women it is m + aF. This formulation allows us to talk of aM and aF as the deviations of men and women, respectively, from some grand overall mean, m, for all people.
A similar formulation can be developed for regression analysis
where the equivalent restriction is applied. Consider the dummy
variable regression model:
yi = b1
+ b3Mi
+ b4Fi
+ ei
(22)
for all individuals i = 1, ..., n.
Now impose the restriction b3 + b4 = 0. This restriction will ensure that b1 will serve as an overall mean for all individuals and that b3 and b4 will serve as the average deviations of men and women, respectively, from that overall mean.
In order to operationalize equation (22) to be able to apply
the least squares method directly, we need to substitute the b3
+ b4 = 0 restriction
into (22). Using b4 = -b3
we can substitute in for b4
and rearrange to get:
yi = b1
+ b3(Mi
- Fi) + ei
(23)
Under this arrangement the average wage for men is b1 + b3 while that for women is b1 - b3. Again it is simple to test for discrimination by testing the null hypothesis HO: b3 = 0 against the alternative HA: b3 > 0.
Alternatively, we could use the weighted averages of the two groups in a restriction b3 + b4= 0. Given = nM and = nF we can rearrange this restriction to get:
b4 = - b3
Substituting this restriction into equation (22) yields:
yi = b1
+ b3 (Mi
- Fi) + ei
(24)
Now, in turn, define b5 such that b3 = nFb5 and the model becomes:
yi = b1 + b5 (nF Mi - nM Fi) + ei (25)
With this set-up, the average wage for men becomes b1
+ nFb5
and that for women becomes b1
- nMb5
so that the men's average wage is higher the more women in the
model and the women's is lower the more men available for work
as long as b5 >
0. The test for discrimination is again the simple matter of
testing the null hypothesis, HO: b5
= 0 against the alternative, HA: b5
> 0.
More interesting problems arise when more complicated patterns
of discrimination are suspected. For example, two different discriminatory
effects may be present: those based on gender and separate effects
based on race. A two-way (gender and race) ANOVA model could
then be specified as:
yijg - m + aj
+ lg + eijg
(26)
where yijg is the average wage of the ith person of the jth gender and gth race, aj is deviations from the average due to gender, lg is deviations due to race, and eijg is the error for the ith person of the jth gender and gth race.
It is important to note that this model is rather restrictive in that it implicitly assumes no interaction between racial and gender discrimination. In other words, the effect on one's wage rate of being black is assumed to be the same regardless of gender. This may not be a valid assumption. Greater racial discrimination might occur if one's gender is male than when one's gender is female. If this is the case, then an interaction term is needed to account for this lack of independence between race and gender.
In the ANOVA model this is easily accommodated by introducing
an interaction term. This produces a two-way ANOVA with interaction
as follows:
yijg = m + aj
+ lg + djg
+ eijg
(27)
The djg term allows for an adjustment when gender alters the degree of racial discrimination, for example.
A comparable model can easily be formulated for regression analysis.
First define Bi = 1 for blacks, Bi
= 0 otherwise; and Wi = 1 for whites, Wi
= 0 otherwise. First specify the two-way regression without interaction
as:
yi = b1
+ b3Mi
+ b4Fi
+ b5Bi
+ b6Wi
+ ei
(28)
This model is, of course, underidentified due to two sets of perfect
multicollinearities (i.e. two singularities in the columns of
the X matrix). These exact linear combinations among the columns
of the X matrix are because b1
is implicitly the coefficient of a ìvariableî that
is always equal to 1 while Mi + Fi
= 1 and Bi + Wi = 1.
Consequently two restrictions must be introduced to identify the
coefficients in equation (28). We could set b3
= 0 and b6 = 0
and make white males the default group with left tail tests for
discrimination (i.e. HO: b4=0
and b5=0 vs HA:
b4<0
and/or b5<0).
However, right tail tests are more convenient so we will instead
impose the restrictions b4=0
and b5=0 to make
black females the default group in the following regression model:
yi = b1
+ b3Mi
+ b6Wi
+ ei
(29)
Thus, to test for gender discrimination test the null hypothesis, HO: b3=0 versus the alternative HA: b3>0. To test for racial discrimination test, HO: b6=0 versus HA: b6>0. To simultaneously test for both gender and racial discrimination test HO: b3=0 and b6=0 against HA: b3>0 and/or b6>0.
The first two tests can be performed with a simple t-statistic. The latter test requires an F-statistic, which in this special circumstance is just the overall F-statistic for the model.
The problem with the regression model specified by equation (29) is that it is too constrained. The starting wage for black men is b1 + b3, which is exactly b3 dollars more than the starting wage for black women, b1. However, the starting wage for white men is b1 + b3 + b6, which is exactly b3 dollars more than the starting wage for white women, b1 + b6. Thus, the difference between black men and women are forced by this model to be exactly the same as the differences between white men and women. This seems unlikely or at least something that should be tested. Unfortunately, the regression model given by equation (29) does not even allow us to test for this possibility.
Just as the difference in the starting wage between men and women implied by equation (29) has just been shown to be a constant difference regardless of race, we now show that racial differences implied by equation (29) are also forced to be a constant difference regardless of gender. To see this, note that the starting wage for white women b1 + b6 is exactly b6 dollars more than that for black women, b1. This model forces the difference between the starting wage for white men, b1+b3+b6 to be exactly b6 dollars more than that for black men, b1 + b3. Again we see that this model imposes an unnatural constraint prior to estimation. Again, the model given by equation (29) is too restrictive to allow us even to test for the prior constraint.
Alternatively, we can make equation (29) more flexible by adding
an interaction term as follows:
yi = b1
+ b3Mi
+ b6Wi
+ b7MiWi
+ ei
(30)
Only white males have access to the b7
dollars in starting salary because b7
enters the model only if Mi=1 and Wi=1.
Thus the racial and gender constraints implied by equation (29)
can be tested by equation (30) merely be performing a t-test of
the null hypothesis HO: b7=0
versus the alternative, HA: b7>0.
Moreover under this new model the starting wage for black men,
(b1+b3),
is b3 dollars more
than the starting wage for black women, b1,
but now the starting wage for white men, (b1+b3+b6+b7),
is b3+b7
dollars more than that for white women, (b1+b6).
Furthermore, the starting wage for white women, (b1+b6),
is b6 dollars more
than the starting wage of black women, b1,
while the starting wage for white men, (b1+b3+b6+b7),
is b6+b7
dollars more than that for black men, (b1+b3).
Thus, the b7 coefficient
of equation (30) has provided full flexibility in freeing up the
constraints of the more restrictive equation (29).
One danger associated with using multiple sets of dummy variables generally and interaction terms in particular is the greater chance of running into problems of perfect multicollinearity with these setups. For example if a particular sample consisted of all men, then applying equation (30) would result in WiMi=1 whenever Wi=1 since Mi would always be equal to one for that sample. In addition Mi=1 would be perfectly multicollinear with the intercept term for the all-male sample. As more and more sets of dummy variables and their interaction terms are introduced into a regression model, the incidence of perfect multicollinearity will increase. This is especially true when sets of dummy variables bring together the effects of race, gender, educational level, occupation and other workplace characteristics because of the high degree of occupational segregation by race, gender and educational level in the U.S. economy. For example, if all nurses in the sample are women and all foremen are men, and vice versa, then at least two perfect multicollinearities will be present.
One way to avoid this problem is to replace the various sets of dummy variables in your model with one larger composite set of dummy variables. The first step is to drop the intercept term out of your model. Next, create a multidimensional table of every categorical combination of characteristics you wish to represent. This may be done using Karnaugh maps. For example, form a Karnaugh map for race versus gender as follows:
Race
| B | W | |||
| Gender | M | 15 | 25 | 40 |
| F | 13 | 27 | 40 | |
| 28 | 52 | 80 |
Next, add a third characteristic such as religion (C=Catholic,
J=Jewish, P=Protestant) so that each new category (religion) has
its own submap.
Figure 3
Religion
| C | J | P | ||||||
| B | W | B | W | B | W | |||
| Gender | M | 2 | 4 | 3 | 5 | 10 | 16 | 40 |
| F | 1 | 6 | 0 | 7 | 12 | 14 | 40 | |
| 3 | 10 | 3 | 12 | 22 | 30 | 80 |
Similarly, high school completion (D=high school diploma, N=no
high school diploma) can be added:
| D | C | J | P | ||||||
| i | B | W | B | W | B | W | |||
| p | D | M | 1 | 3 | 2 | 5 | 6 | 13 | 30 |
| l | F | 0 | 3 | 0 | 6 | 7 | 8 | 24 | |
| o | N | M | 1 | 1 | 1 | 0 | 4 | 3 | 10 |
| m | F | 1 | 3 | 0 | 1 | 5 | 6 | 16 | |
| a | 3 | 10 | 3 | 12 | 22 | 30 | 80 |
In general, composite dummy variables are created for each nonempty
cell. For Figure 2 create four dummy variables: MBi=1
if male black, MBi=0 otherwise; MWi=1
if male white, MWi=0 otherwise; FBi=1
if female black, FBi=0 otherwise; and FWi=1
if female white, FWi=0 otherwise. Having
dropped out the intercept term, this leads to the following regression
model:
yi = a1MBi
+ a2MWi
+ a3FBi
+ a4FWi
+ ei (31)
This approach provides the extremist solution to the multicollinearity problem discussed above by ensuring that these dummy variables are all orthogonal to one another (i.e. have exactly zero correlation among them) since all groups are now mutually exclusive. Since we are assuming that our sample consists of only people with zero experience (i.e. Xi=0), then each coefficient represents the average starting wage for that particular group. In other words, male blacks average a1 dollars as their starting wage, while male whites average a2 dollars, female blacks average a3 dollars and female whites average a4 dollars.
Figures 3 and 4 demonstrate how to expand the Karnaugh maps to include additional characteristics (religion and high school completion). Note that as more characteristics are added, more cells with zero elements appear. Since dummy variables are created only for nonempty cells, the cells with zero elements are ignored. This is equivalent to bypassing the multicollinear situations.
Composite dummy variables as used in equation (31) are situational. That is to say, each dummy variable represents a complete situation rather than just one characteristic. This means that it is easy to test for the significance of a particular subgroupís starting wage (relative to zero or some other constant), but we canít test for a single characteristic such as race using the standard student-t test. For example if we wish to test to see if blacks are discriminated against in starting wage, we need to test the null hypothesis, HO: a1 = a2 and a3 = a4 versus the alternative HA: a1 _ a2 and/or a3 _ a4. This requires an F-test since for this situational model, the null hypothesis involves two constraints rather than just one. In this case, the F statistic has two numerator degrees of freedom (the number of restrictions) and n-k denominator degrees of freedom, where k is the number of estimated parameters which is equal to 4 for the situational model depicted in equation (31).
The test statistic is calculated by running two regressions: an unrestricted regression and then a restricted regression. The unrestricted regression is just the one given by equation (31), while the restricted regression is equation (31) with a2 and a4 each set equal to zero (i.e. drop a2 and a4 out of the equation and replace MBi with Mi = MBi + MWi and FBi with Fi = FBi + FWi) but the full set of observations are used in running both of these regressions.
Define:
SSEU = 2 (32)
SSER = 2 (33)
where 1, 2, 3,
and 4 refer to the unrestricted least squares
estimates and 1 and 3
refer to the restricted least squares estimates (i.e. simply
the least squares estimates obtained after dropping MWi
and FWi out of the model). The appropriate
F-statistic for testing for discrimination against blacks is then:
~ F-4 (34)
Note that the degrees of freedom for the chi-square variable is
n-2 while has n-4 degrees of freedom so has (n-2) - (n-4) = 2
degrees of freedom. Since the chi-square in the denominator has
n4 degrees of freedom, then the s2
cancel each other out, and we have an F-statistic with 2 numerator
degrees of freedom and n-4 denominator degrees of freedom. For
small values of this F-statistic we will not reject the null hypothesis
of equality and for large values we will reject HO
(see F-table at some specific level of significance for a more
exact cutoff value).
Thus far we have only considered adjustments to the intercept which, in our example, measures discrimination in the starting wage. But what if Sexism Incorporated starts everyone out at the same starting wage but then increases menís wages at a faster rate than womenís? How do we establish and then test the difference in the rate of increase in the wage rate for men versus women?
First of all we will need years of experience, Xi,
in our regression, so we begin with the basic model:
yi = b1
+ b2Xi
+ ei
(35)
As before we use the dummy variable Mi for
men and Fi for women, but now we use them
to adjust the slope rather than the intercept.
yi = b1
+ b2Xi
+ b3MiXi
+ b4FiXi
+ ei (36)
Again the problem of perfect multicollinearity appears because
Xi = MiXi +
FiXi so we have an exact
linear combination among the explanatory variables. Some restriction
must be imposed. One obvious one is b2
= 0 so that b3
and b4 are left
to serve as the rates of wage increase for men and women, respectively.
yi = b1
+ b3MiXi
+ b4FiXi
+ ei (37)
This model has the advantage of directly generating estimates
of the rate of wage increases for each group separately. Its
disadvantage is in testing for across-group differences since
such a test will involve two coefficients (HO:
b3 = b4)
as opposed to just one coefficient (HO: b3
= 0) for the model:
yi = b1
+ b2Xi
+ b3MiXi
+ ei (38)
In this latter model, b4 has been restricted (b4 = 0) instead of b2. Women now serve as the default group and b2 now represents their rate of increase in wage rate while that for men is b2 + b3. Consequently, the test for differences in rate of wage increases is just a student-t test of b3 with null hypothesis HO: b3 = 0 and alternative hypothesis HA: b3 > 0.
Some researchers prefer to have b2
represent an average rate of increase over all groups of individuals
instead of serving as the rate of increase for some designated
default group. If b2
is to be an average rate of increase over equally weighted groups,
then the appropriate restriction to be placed on equation (36)
for our example would be:
b2 =
Multiplying through both sides with a 2 and canceling the b2ís
yields: 0 = b3
+ b4 or b4
= -b3. This results
in the equation:
yi = b1
+ b2Xi
+ b3(MiXi
- FiXi) + ei
(39)
The specification in equation (39) makes b2 the average rate of increase of the straight (unweighted) group averages. This test for equality (HO: b3 = 0) versus discrimination favoring men (HA: b3 > 0) is the standard one-sided studentt test for b3.
To make b2 the
average rate of increase for the weighted group averages, or,
equivalently the overall average of the individual observations,
we must impose the restriction:
b2 = (40)
on equation (36). By multiplying through both sides of equation (40) by n and noting that nM + nF = n, we can cancel the b2ís to get 0 = nMb3 + nFb4 which can be written as
b4 = b3
. Substituting this restriction into equation 36 yields:
yi = b1
+ b2 Xi
+ b3 ( Mi
Xi - Fi Xi)
+ ei (41)
Again, a simple student-t test on b3
is all that is required to test for discrimination.
Under mounting pressure from its critics, Sexism Incorporated has instituted an affirmative action plan for women. The company claims that it starts women out at a higher wage than men when both have no experience (Xi = 0). How do we test to determine if this is in fact the case? Moreover, what if the company starts women at a higher wage but then promotes men faster? Under that circumstance, the menís wage might quickly surpass the womenís, even when the women started out at a higher wage. In other words, is there a Sexism Incorporated affirmative action fake-out plan?
First, letís reconsider the starting wage differences discussed earlier but now in the context of controlling for months of experience. Previously we assumed that all individuals in our sample had zero months of experience. What if this is not the case? What if experience differs substantially over the sample? Does this invalidate the results of our previous analysis?
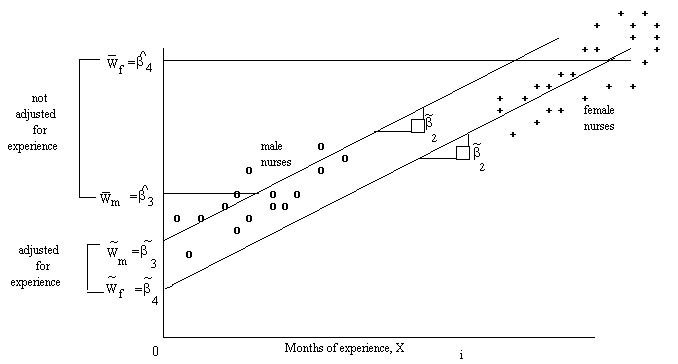
To get a better perspective on these questions, consider the hospitals owned by Sexism Incorporated. Assume that we have carried out an analysis of the wage rates of male and female nurses that ignores differences in experience. Under these circumstances, we have obtained statistically significant t-statistics for the difference between female and male nursesí wages that shows that male nurses are discriminated against in that they have significantly lower wages than female nurses. Figure 5 shows this situation with the observations on male nurses clustered at the lower left and those for female nurses clustered at the upper right of the diagram.
The old model that ignored experience may be expressed as:
yi = b3Mi
+ b4Fi
+ ei
(42)
Since Mi and Fi have zero
correlation, then least squares will estimate each coefficient
to be equal to the average age of each of the two groups (males
and females) respectively (i.e. 3
= m and 4
= f). Even if the student-t test for 4
- 3 finds the females to have a statistically
significantly higher average wage than the males, we may reject
this evidence as invalid if males and females do not have essentially
the same average months of experience. Figure 5 depicts exactly
this situation. Since female nurses average substantially more
months of experience than male nurses, their average wage is substantially
greater as well. Of course, the real question is: How do the
wages of male and female nurses compare once we control for experience?
Will the evidence still support the hypothesis that male nurses
are discriminated against? To control for experience, we merely
need to include the variable Xi, months of
experience, as an explanatory variable in our regression as follows:
yi = b2Xi
+ b3Mi
+ b4Fi
+ ei (43)
As displayed in Figure 5, the appropriate average wage rates after controlling for experience are the same as the least squares estimates of b3 and b4 from equation (43), in other words, M = 3 and F = 4 where 3 and 4 are the corresponding least squares estimates.
The difference between 3 and 4
suggests that it is the female nurses who are actually being discriminated
against and not the male nurses since the male nurses have a significantly
greater starting wage after controlling for differences in
months of experience. However, the model forces the two groups
to have exactly the same rate of increase in wage rates. This
might be unrealistic. Even if two groups have the same starting
wage, one groupís wage rate could quickly exceed the otherís
if it had a higher rate of increase (i.e. steeper regression slope).
To allow for both differences in intercepts and differences in
slope, the general model may be written as:
yi = b1
+b2Xi
+ b3Mi
+ b4Fi
+ b5MiXi
+ b6FiXi
+ ei (44)
To avoid perfect multicollinearity, we must impose two restrictions:
one restriction on the intercept parameters and one restriction
on the slope parameters. A convenient set of such restrictions
is b1 = 0 and b2
= 0. These two restrictions transform equation (44) into a model
that provides direct expressions for the separate intercepts and
separate slopes of men and women.
yi = b3Mi
+ b4Fi
+ b5MiXi
+ b6FiXi
+ ei (45)
Within the context of this model, Figure 6 depicts the deceptive
ìaffirmative actionî plan of Sexism Incorporated.
Although Sexism Incorporated does start women out at a higher salary, the men are promoted (on average) much more quickly than the women (on average) so the actual average menís wage quickly exceeds that of the women. Only this more flexible model can accurately sort out these behaviors and reveal what is really going on here. Tests for differences in intercepts or for differences in slopes can be performed, or a test for the joint effect of intercept and slope differences together can be carried out.
As before, the standard test for intercept differences is a t-test with standardized test statistic which in this case has n-4 degrees of freedom. Similarly, the test for differences in slope uses the student-t statistic which again has n-4 degrees of freedom.
To test for both slope and intercept differences together, we
must use an F-test because the null hypothesis will involve two
restrictions (HO: b4-b3=0
and b5b6=0)
and student-t test can only test one restriction at a time. Of
course, squaring a student-t statistic gives a special case of
the F-test where the F-statistic so generated has only one numerator
degree of freedom and n-k (n-4 in the example) denominator degrees
of freedom. The F-test is carried out by first calculating the
error sum of squares for equation (45):
SSEU = 2
Next, impose the restriction implied by the null hypothesis HO:
b4=b3
and b5=b6
to produce the model:
yi = b3(Mi
+ Fi) + b5(MiXi
+ FiXi) + ei
or, since Mi + Fi = 1,
we have simply:
yi = b3
+ b5Xi
+ ei
(46)
Thus the restricted sum of squares implied by this null hypothesis
is
SSER = 2
where 3 and 5 are obtained
by simply applying least squares estimation to equation (46).
Thus the appropriate F-statistic for the null hypothesis HO:
b4 = b3
and b5
= b6 against
the alternative HA: b4
b3 and/or
b5 b6
is:
~ F
It would be desirable to have a more directional alternative hypothesis that addressed discrimination questions such as are women being discriminated against, which suggests the alternative HA: b3 > b4 and/or b5 > b6. Unfortunately, the F-test does not easily lend itself to this type of more refined alternative. Future research may allow for a Bayesian multidimensional posterior odds ratio solution to this problem.
An alternative formulation of this more flexible discrimination
model that allows for an easier, more direct testing for discrimination
can be obtained by imposing the alternative restrictions b4
= 0 and b6 = 0
on equation (44) to get:
yi = b1
+ b2Xi
+ b3Mi
+ b5MiXi
+ ei
(47)
Now testing for differences in starting salary is simply a matter of checking the t-statistic associated with 3, which is ~ t n-4. This provides a test of the null hypothesis HO: b3 = 0 against an alternative of discrimination against women, HA: b3 > 0.
Similarly, testing for discrimination against women in rate of increase in salary is performed using the standardized test statistic ~ tn-4 to test HO: b5 = 0 against HA: b5 > 0.
However, even with the default group specification of the model,
we are still limited to the more general overall test of the joint
null hypothesis HO: b3 = b5 = 0
against the two-sided alternative HA:
b3 _
0 and/or b5 _
0 (i.e. HO not true). As in the preceding
model, the test statistic is:
~ F
except that now the definitions of SSEU and
SSER are changed to:
SSEU =
and
SSER = .