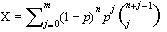
Introduction
Business and government agencies often use surveys to obtain information about consumers or other groups. The individuals who fill out these surveys are not always willing or able to answer all questions. Often such missing data are assumed to be missing-at-random.
If the data are not missing-at-random, statistical analyses may be distorted and generate reports that are misleading.
We provide a test to determine if survey data are missing-at-random. For data that are not missing-at-random, we provide a method of correcting the probability distribution of the response variables for the systematic pattern in the missing data. Previous studies used time-series, panel data or the ordinal nature of responses to provide the structure for handling systematically missing data (see Fitzmaurice et al.(1996)). Davis(1993) presented useful methods for the case when all of the independent variables are categorical. Our method uses cross-sectional data with nominal responses and both nominal and continuous independent variables. This methodology simply uses a joint probability distribution framework. It can be extended to incorporate both detailed and aggregated responses so that all observations can be used without sacrificing any of the detail. We require the response outcomes to be mutually exclusive and exhaustive in the form of a composite variable. Specifically, this paper provides a methodology using SAS® CATMOD, REG, NLIN and IML to produce distributions of the missing variable probabilities and GPLOT to produce graphs of the difference between the probability distributions with and without adjusting for the missing data, thereby providing a visual check of the nature of the missing responses.
We examine a survey of different types of businesses in downtown Minneapolis measuring their satisfaction with downtown conditions, services, etc. This survey was in conjunction with the first author's dissertation (see Baxter(1994)). One question on the survey required self-reporting of the type of business as a check on the Dun's database categorization used to acquire addresses. Coders later transformed the responses to standard industrial classification (SIC) codes. Fourteen percent of these responses were left blank. The authors faced the all-too-common research dilemma of either throwing away the observations when the SIC code was missing or ignoring this check all together and trusting that the current designation according to Dun's database was correct. Preliminary investigation had indicated a fairly large discrepancy between the two.
The Problem of Missing Survey Data
Missing data can pose a significant problem when the goal is to understand the behavior of all subjects rather than just the ones with complete data. Often researchers have simply ignored missing data with the hope that they are missing-at-random. Unfortunately, data are frequently systematically missing in a non-ignorable manner that can lead to substantial distortions when only complete data are used. Some researchers have estimated models with the complete data and then used the estimated model to fill in the missing data. Using predicted values for the missing data simply covers up rather than explains the systematic nature of the missing data. A more constructive approach in this context has been to hypothesize a model for the complete data, Yi1 = f(Xi1,b1) + ei1 , a model for the missing data, Yi0 = f(Xi0,b0) + ei0, and a latent variable model explaining the difference between missing and nonmissing status, Ii1 = f(Zi,d) + ni.
It is important to note that even in the special case where the X's and the b's are the same, the distribution of the errors may be quite different. Therefore, econometricians have focused on determining the distribution of the triple {ei0, ei1,ni}. On the other hand, statisticians have viewed this problem as one involving a mixture of the error distributions.
In this paper, the problem is a special case where outcomes are
discrete random variables and multinomial probabilities form the
basis of the data generating process. Consequently, we are able
to bypass the latent variable approach and focus directly on the
joint probability structure. In this case, the joint probabilities
are broken down into two sets. One set of joint probabilities
is observed and the second set is unobserved (missing). If we
were just interested in behavior of those with observed observations
and if group membership was determined strictly by exogenous variables,
then we would be content with knowing the joint probability structure
for the observed observations alone. This would also be satisfactory
if group differences were ignorable and the missing data were
truly missing-at-random. Since we know which observations have
missing data, we have a censored rather than a truncated distribution.
Since we test for data to be missing-at-random (MAR) and not
missing-completely-at random (MCAR), we have to control for whatever
independent variables are needed to ensure that the model errors
have mean zero. For further discussion of this issue see Rubin(1976).
An Analysis of the Joint Multinomial Density
The probability of an observation being missing may be viewed
as the sum of the probabilities of the unobserved outcomes. In
other words, the probability of being missing is simply the marginal
probability corresponding to the outcome designated "missing"
for a discrete random variable representing "missing"
versus "observed" status.
Figure 1. Multinomial Probabilities for Observed Outcomes Only
| Group 1 | Group 2 | Group 3 | Group 4 | Group 5 | Group 6 | Group 7 | Missing |
|---|---|---|---|---|---|---|---|
| P10i | P20i | P30i | P40i | P50i | P60i | P70i | Pmi |
Figure 2. Joint Multinomial Probabilities for Observed/Unobserved
| Group 1 | Group 2 | Group 3 | Group 4 | Group 5 | Group 6 | Group 7 | |
|---|---|---|---|---|---|---|---|
| observed | P10i | P20i | P30i | P40i | P50i | P60i | P70i | P0i |
| missing | P1mi | P2mi | P3mi | P4mi | P5mi | P6mi | P7mi | Pmi |
| P1i | P2i | P3i | P4i | P5i | P6i | P7i | 1.0 |
The objects of interest here are the marginal probabilities on
the bottom line of Figure 2 which are obtained by summing over
the corresponding observed and missing joint probabilities. If
the missing data are missing-at-random, then for each observation
the missing joint probabilities will just be some constant multiple,
Ci of the observed joint probabilities (i.e. constant over the
alternatives). However, if the missing data are not missing-at-random,
then separate Cji's must be estimated for each of the j = 1,
. . . ,7 alternatives as shown in Figure 3.
Figure 3. Joint Multinomial Distribution of Observed Probabilities
| Group 1 | Group 2 | Group 3 | Group 4 | Group 5 | Group 6 | Group 7 | |
|---|---|---|---|---|---|---|---|
| observed | P10i | P20i | P30i | P40i | P50i | P60i | P70i | Poi |
| missing | C1i P10i | C2iP20i | C3iP30i | C4iP40i | C5iP50i | C6iP60i | C7iP70i | Pmi |
| P1i | P2i | P3i | P4i | P5i | P6i | P7i | 1.0 |
In the context of this framework the problem becomes one of appropriately estimating the Cji terms. For example, a simple structure for this problem would be Cji = Cj i.
The Cj provides weights appropriate for the j = 1, ..., J outcomes
while the i provides the necessary observation specific adjustment
to ensure the condition:
C1 hi P1oi
+ C2 hi P2oi
+ C3 hi P3oi
+ C4 hi P4oi
+ C5 hi P5oi
+ C6 hi P6oi
+ C7 hi P7oi
= Pmi (1)
Our procedure in this case is straightforward. Since for each observation the original data generates a value of one for the outcome that occurs and a zero for each of the other outcomes, it is easy to estimate the corresponding multinomial logistic probabilities corresponding to those in Figure 1. Applying a least squares regression of Pmi onto all of the other probabilities in equation (1) with no intercept term produces estimates of the Cj's. The fitted equation for the predicted values for Pmi are then multiplied by the appropriate i value necessary to ensure the equality in equation (1) and, thus, to fully restore the original Pmi value for each of the i=1,...,n observa-tions. Thus, the i value serves as the sample realization of the population error, or, in other words, a residual term. The null hypothesis, Ho: C1 = C2 = C3 = C4 = C5 = C6 = C7 can be used to test the missing-at-random assumption. A rejection of this hypothesis supports the claim that the data are not randomly missing and, therefore, in that case, imposing the missing-at-random assumption could produce misleading estimates of the corresponding marginal probabilities.
Analyzing the Minneapolis Survey Data
Because we are dealing with a polychotomous dependent variable
and both continuous and nominal independent variables, we utilize
the multinomial logit response function in PROC CATMOD. We chose
a large number of control variables (thirty in all) in an effort
to satisfy the zero mean assumption in the error term. These
variables, indicated in Figure 4, included number of employees
as a continuous variable, location of primary market as four
independent dummy variables, and the importance of various downtown
characteristics such as cost of space and access to parking ramps
as 26 independent variables each with four response levels/magnitudes
which we treated as continuous for this study. The SIC's were
grouped into seven industry sectors which with the missing response
category provided eight possible responses to serve as the dependent
variable for our multinomial logistic model. This model was then
estimated using PROC CATMOD which produced the following analysis
of variance table:
Figure 4. Analysis of Variance Table from PROC CATMOD
MAXIMUM-LIKELIHOOD ANALYSIS-OF-VARIANCE
TABLE
| Source | |||||||
| CONSTANT | |||||||
| Q018A1 | primary mkt in Minneapolis | ||||||
| Q018A2 | in twin cites outside Mpls | ||||||
| Q018A3 | in MN but outside of TC's | ||||||
| Q018A4 | outside of Minnesota (MN) | ||||||
| Q004A | |||||||
| Q025A | |||||||
| Q025B | |||||||
| Q025C | |||||||
| Q025D | |||||||
| Q025E | |||||||
| Q025F | |||||||
| Q025G | |||||||
| Q025H | |||||||
| Q025I | |||||||
| Q025J | |||||||
| Q025K | |||||||
| Q025L | |||||||
| Q025M | |||||||
| Q025N | |||||||
| Q025O | |||||||
| Q025P | |||||||
| Q025Q | |||||||
| Q025R | |||||||
| Q025S | |||||||
| Q025T | |||||||
| Q025U | |||||||
| Q025V | |||||||
| Q025W | |||||||
| Q025X | |||||||
| Q025Y | |||||||
| Q025Z | |||||||
| 5796 | chi-square: | 2737.03 | |||||
Since the focus of this paper is on the probability distributions
and not on the regression coefficients, we will not present the
details of each of the seven logistic equations that were produced
here. Rather, Figure 5 presents the results of regressing the
probability of falling into the missing data cell onto the other
seven probabilities: OP1, OP2, OP3, OP4, OP5, OP6 and OP7.
Figure 5. PROC REG of Probability of Missing onto the Other
Seven Probabilities
| Source | |||||||||||||||||||||||||||||||||||||||
| Model | |||||||||||||||||||||||||||||||||||||||
| Error | |||||||||||||||||||||||||||||||||||||||
| U Total |
Root
MSE
| Dep
Mean
|
| | |||||||||||||||||||||||||||||||||||
Group Variable Parameter DF Estimate Error Parameter=0 Prob > |T|
Group1: OP1 C1 1 0.290663 0.06714980 4.329 0.0001
Group2: OP2 C2 1 0.205629 0.04876047 4.217 0.0001
Group3: OP3 C3 1 0.269572 0.06617726 4.073 0.0001
Group4: OP4 C4 1 0.520265 0.04241483 12.266 0.0001
Group5: OP5 C5 1 0.042962 0.03278431 1.310 0.1904
Group6: OP6 C6 1 -0.016225 0.04004514 -0.405 0.6855
Group7: OP7 C7 1
0.091259 0.02875196 3.174 0.0016
Notice that no intercept was used in this regression since it would be inappropriate given the statistical theory discussed in the previous section. The estimated regression coefficients are all positive and statistically significantly greater than zero as expected except for the fifth one which is positive but not significantly greater than zero and the sixth one which has a negative sign but is not statistically significant.
In order to determine whether the marginal probabilities implied
by the above regression results indicate that the missing data
are missing-at-random or not, we ran a regression that restricted
the coefficients in the above model to all be equal (still with
no intercept) where PCOMBINE = (OP1 + OP2 + OP3 + OP4 + OP5 +
OP6 + OP7). This enabled us to run the restricted regression
where the fitted value of Pmi is equal to an
estimate of the common coefficient C times PCOMBINE: fitted
Pmi = C (P1oi+P2oi+P3oi+P4oi+P5oi+P6oi+P7oi).
Figure 6. Restricted PROC REG of Probability of Missing
onto the Combined Probability Variable
Sum of Mean
Source DF Squares Square F Value Prob>F
Model 1 19.84560 19.84560 620.782 0.0001
Error 859 27.46115 0.03197
U Total 860 47.30675
Root MSE 0.17880 R-square 0.4195
Dep Mean 0.18140 Adj R-sq 0.4188
C.V.
98.56815
Parameter Standard T for H0:
Variable DF Estimate Error Parameter=0 Prob > |T|
PCOMBINE C 1 0.182584
0.00732812 24.915 0.0001
Figures 5 and 6 provide
the information necessary to carry out a conditional test of the
null hypothesis that the missing data are missing-at-random.
A conditional F-statistic can be computed treating the nonmissing
probability variables as exogenous (independent) variables in
the regressions reported in Figures 5 and 6. This ignores the
first stage which was the logistic (PROC CATMOD) stage of the
analysis so it does not qualify as a legitimate unconditional
test for randomness. This conditional or pseudo F-statistic can
be calculated using the standard F value for testing a linear
restriction on a "linear" model using error sums of
squares (SSE) from the restricted , R, and unrestricted, U, regressions
and corresponding degrees of freedom (df) as follows:
With 6 numerator degrees of freedom and 853 denominator degrees of freedom, at a 0.01 level of significance the Table-F value is approximately 2.80, and, therefore, the missing-at-random hypothesis is rejected. This confirms our suspicion that missing-at-random was not a good assumption here. However, one disturbing aspect of the results in Figure 5 is the negative sign for C6. Even though in this case this negative value is not even close to being statistically significant at any of the usual levels of significance, clearly negative values for these parameters are inappropriate. Instead of dealing with these negative values on an ad hoc basis, it would be better to impose the restriction that the Cj's must be positive. A simple way of imposing this restriction is to define a new parameter j = ln(Cj) for j = 1, . . . , J.
This simply means replacing the Cj's in the least squares regression
above with exp(j) and estimating the resulting regression using
nonlinear least squares. The starting values for the j's are
the natural logs of the corresponding Cj's. In the cases where
negative values were initially obtained for any of the Cj's, the
OLS regression was first rerun with the negative Cj values set
to zero (dropped out those variables) to obtain new starting values
more consistent with the nonnegative restriction before running
the nonlinear least squares regression for that group. The nonlinear
least squares results are presented in Figure 7.
Figure 7. The Results of the PROC NLIN
Non-Linear Least Squares Iterative Phase
Dependent Variable OPZ999
Method: Marquardt
NOTE: Convergence criterion
met.
Non-Linear Least Squares Summary Statistics
Dependent Variable PMISS
Source DF Sum
of Squares Mean Square
Regression 6 23.082111446 3.847018574
Residual 854 24.224640659 0.028366090
Uncorrected Total 860 47.306752106
(Corrected Total) 859 19.009077722
NOTE: The Jacobian is singular.
Parameter Estimate Asymptotic Asymptotic 95 % corresponding
Std. Error Confidence Interval C-value
Lower Upper
A1 -1.2466842 0.231858449 -1.70177097 -0.79159746 0.287456
A2 -1.5816872 0.237013610 -2.04689244 -1.11648204 0.205628
A3 -1.3081609 0.244599426 -1.78825537 -0.82806642 0.270317
A4 -0.6622891 0.079217914 -0.81777627 -0.50680184 0.515670
A5 -3.2798392 0.797587280 -4.84532630 -1.71435210 0.037634
A6 -372.2241151 0.000000000 -372.22411509 -372.22411509 0.000000
A7 -2.4047374 0.317181541
-3.02729452 -1.78218035 0.090289
Asymptotic
Correlation Matrix
Corr A1 A2 A3 A4 A5 A6 A7
-----------------------------------------------------------------
A1 1 -0.0929 -0.5683 -0.3208 -0.1073 . 0.0935
A2 -0.0929 1 -0.0796 -0.0946 -0.1420 . -0.1380
A3 -0.5683 -0.0796 1 0.0635 -0.1581 . -0.1366
A4 -0.3208 -0.0946 0.06351 1 -0.2568 . -0.2838
A5 -0.1073 -0.1420 -0.15815 -0.2568 1 . -0.0126
A6 . . . . . . .
A7 0.09355 -0.1380 -0.1366 -0.2838 -0.0126 . 1
The Jacobian was singular for the asymptotic variance-covariance
matrix so a conditional Wald test statistic could not be calculated
to test the hypothesis that all seven coefficients are equal because
of the A6 coefficient. However, it is possible to generate a
conditional Wald statistic to test the hypothesis that the other
six groups all have the same population coefficient value.
Figure 8. PROC IML Code for Conditional Wald Test for Missing-at-Random
354 proc iml;
IML Ready
355 a1= -1.2466842;
356 a2= -1.5816872;
357 a3= -1.3081609;
358 a4= -0.6622891;
359 a5= -3.2798392;
360 a7= -2.4047374;
361 first= a1||a2||a3||a4||a5;
362 second= a2||a3||a4||a5||a7;
363 pre=first - second;
364 v={0.231858449 0.237013610 0.244599426 0.079217914 0.797587280 0.317181541};
365 D=diag(v);
366 CORR={ 1 -0.0929 -0.5683 -0.3208 -0.1073 0.0935,
367 -0.0929 1 -0.0796 -0.0946 -0.1420 -0.1380,
368 -0.5683 -0.0796 1 0.0635 -0.1581 -0.1366,
369 -0.3208 -0.0946 0.0635 1 -0.2568 -0.2838,
370 -0.1073 -0.1420 -0.1582 -0.2568 1 -0.0126,
371 0.0936 -0.1380 -0.1366 -0.2838 -0.0126 1};
372 cov=D*CORR*D;
373 AU={1 -1 0 0 0 0, 0 1 -1 0 0 0, 0 0 1 -1 0 0,
0 0 0 1 -1 0, 0 0 0 0 1 -1};
374 w=pre*inv(au*cov*au`)*pre`;
374 prob=1-probchi(w,5);
375 print first second pre
v d corr cov au; print w; print prob;
The Wald Test Statistic value is 51.777303 for the null hypothesis Ho: A1 = A2 = A3 = A4 = A5 = A7. With five degrees of freedom the table value for the chi-square is 11.07 at the 0.05 level of significance and 15.086 at the 0.01 level. Again, as in the case of the linear model, the null hypothesis that the data were missing-at-random is rejected.
The calculations above have enabled us to distribute the missing data probability to probabilities associated with the other outcome categories. Having done this we were then able to combine the observed and missing probabilities to get rid of the observed and missing data categories altogether. By this method, we recover the marginal distribution with probabilities that represent the full population and not just its observed members.
Figure 9. Adjustments to the Original
Probabilities (plot
of diff = final minus original)
Group 1: Transportation-Utilities-Wholesale Group 2: Non-profit Organizations
Group 3: Mining and Manufacturing Group 4: Finance,
Insurance, Real Estate
Group 5: Business Services Group 6: Engineering
Group 7: Education and Social Services
Interpreting PROC GPLOT Graphs of Probability Differences (Final
minus Original)
Figure 9 on the next page shows the adjustments that were made to the original probabilities. The horizontal line at 0.00 represents the base line before adjustment. The monotonically increasing line represents the change in the probability of a firm being in a particular industrial classification that occurs when taking into account the effects of the missing data. Note that these are plots of the conditional means and not plots of the error distribution. The amount of the adjustment varies from observation to observation so the data were ordered by the amount of the needed adjustment before the data were plotted. Since the measurement is final probability minus original probability, values above the 0.00 line represent upward adjustments while those below the 0.00 line are downward adjustments.
The first three industry groups which include Transportation, Utilities, Wholesale, Mining, Manufacturing and Non-profit Organizations (Groups 1, 2 and 3) show rather minor adjustments with most in the middle range showing that virtually no adjustment was needed but with a few at either end (especially the upper end) showing some, but still relatively small, adjustments were needed.
However, the industrial group (Group 4) consisting of Finance, Insurance and Real Estate required consistently positive adjustments which were large in some cases. This suggests that this group was underrepresented in the observed data by virtue of being overrepresented in the missing data. In fact, the statistics reported in Figure 10 confirm that all of the adjustments for this group were positive with at least one adjustment as high as 0.27.
One the other hand, the last three graphs in Figure 9 representing
Business Services, Engineering, Education and Social Services
(Groups 5, 6 and 7) show that predominantly negative adjustments
were needed (as much as -0.25 in Engineering) with a few barely
visable exceptions as confirmed by the last column in Figure 10.
This suggests that the proportion of these types of businesses
was overstated by the originally observed (nonmissing) data.
Figure 10. Adjustments to the Original Probabilities (PROC
MEANS)
Variable N Mean Std Dev Minimum Maximum
--------------------------------------------------------------------
GROUP1 860 0.0076355 0.0113956 -0.0300980 0.0612586
GROUP2 860 -0.0001481 0.0077354 -0.0860430 0.0311354
GROUP3 860 0.0055269 0.0096257 -0.0383066 0.0678353
GROUP4 860 0.0470900 0.0458737 0.0001259 0.2719392
GROUP5 860 -0.0224777 0.0250306 -0.1600833 0.0016888
GROUP6 860 -0.0251142 0.0297314 -0.2514728 -5.903096E-6
GROUP7 860 -0.0125124 0.0187359 -0.1338352 0.0070185
--------------------------------------------------------------------
The danger inherent in summary statistics such as those in Figure
10 (PROC MEANS) is in missing the intrinsically nonlinear nature
of the data distribution which can be seen so clearly in the ordered
(PROC SORT) data graphs (PROC GPLOT). Researchers are tempted
to try to interpret a nonlinear model by looking at the average
effect of a variable when all other variables are held at their
means (or medians). The problem with this approach is that the
group implied by this averaging process may not even approximately
exist. Such an approach runs the danger of developing policy
recommendations that turn out to benefit no one and ignore individual
differences that reflect the real behavioral patterns inherent
in the data.
Summary and Conclusions
In this paper we have demonstrated a method of testing and correcting for distortions in the probability distribution of categorical response data that have some missing values when the data include both continuous and categorical independent variables. In particular, we have applied these methods to survey data of businesses in downtown Minneapolis to correct for distortions in the observed (nonmissing) frequency data for seven types of business categories that were based on SIC codes. We have determined through the use of conditional F and Wald tests that the missing data are not missing-at-random. We then corrected the probability distribution for the distortions caused by the nonrandom nature of the missing data. PROCs CATMOD, NLIN and IML serve as useful tools for applying this method of analysis.
Moreover, we has also demonstrated a graphical way of displaying the differences in conditional group membership probabilities that more fully takes advantage of the nonlinear information inherent in this analysis. While PROC MEANS provides a useful but limited summary of the data, PROC SORT and PROC GPLOT give us additional important information when interpreting the results of nonlinear statistical analysis.
References
Baxter, Shelley S. (1994), Producer Services and the
Corporate Headquarter Complex: A Minneapolis Case Study, Ph.D.
dissertation, Department of Economics, University of Notre Dame.
Chilko, Daniel M. (1983), SAS® Technical Report
A-106: Probability Plotting, SAS Institute, Inc.
Davis, Charles S. (1993), "Analysis of Incomplete
Categorical Repeated Measures", Proceedings of Midwest
SAS® Users Group, vol. 4, 1993, pages 197 - 202.
Fitzmaurice, Garrett M., Nan M. Laird and Gwendolyn E. P. Zahner
(1996), "Multivariate Logistic Models for Incomplete
Binary Response", Journal of the American Statistical
Association, vol. 91, no. 433, March 1996, pages 99 - 108.
Marsh, Lawrence, Maureen McGlynn and Debopam Chakraborty (1994)
"Interpreting Complex Nonlinear Models", Proceedings
of SAS® User's Group International, vol. 19, 1994, pages
1185 -1189.
Marsh, Lawrence and Karin Wells (1994) ìTransforming
Data, Restructuring Data Sets, Creating Look-Up Tables, and Forming
Person-Year Records for Event History Analysisî, Proceedings
of Midwest SAS® Users Group, vol. 5, 1994, pages 260 -
266.
Marsh, Lawrence and Karin Wells (1995) ìKarnaugh
Maps, Interaction Effects, and Creating Composite Dummy Variables
for Regression Analysis", Proceedings of SAS® User's
Group International, vol. 20, 1995, pages 1194 -1203.
Marsh, Lawrence and Karin Wells (1996) ìAn Analysis
of Changes in the Public Employment of Black Women, White Women,
Black Men and White Men Using a New Method of Accounting for Missing
Data on Job Loss Status", working paper presented
to the Midwest Economics Association, Chicago, March 1996,19
pp.
Rubin, Donald B. (1976), "Inference and Missing Data",Biometrika,
vol. 63, 1976, pages 581-592.
So, Ying and Warren R. Kuhfeld (1995), "Multinomial Logit Models", Proceedings of the SAS® Users Group International, vol. 20, 1995, pages 1227-1234.