Using Lagrange Multipliers to Solve a Constrained Max-Min Problem

Contents

Space probe

A space probe in the shape of the ellipsoid

$$4x^2+y^2+4z^2=16$$

enters the earth's atmosphere and its surface begins to heat. After 1 hour the temperature at the point (x,y,z) on the probe's surface is

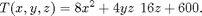
$$T(x,y,z) = 8x^2+4yz-16z+600. $$

Find the hottest point on the probe's surface.

Step1 Write the constraint as g = 0. The function g is

syms x y z
g = 4*x^2+y^2+4*z^2-16

 
g =
 
4*x^2 + y^2 + 4*z^2 - 16

Step 2 The extreme values of T on the probe's surface occur where the gradients of T and g are parallel. We set up the equations

T = 8*x^2+4*y*z-16*z+600

 
T =
 
8*x^2 - 16*z + 4*y*z + 600
 

gradg = jacobian(g,[x,y,z])
gradT = jacobian(T,[x,y,z])

 
gradg =
 
[ 8*x, 2*y, 8*z]
 
 
gradT =
 
[ 16*x, 4*z, 4*y - 16]

We need to solve the equations

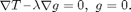
$$ \nabla T \,\mbox{--}\,\lambda \nabla g = 0, \ g=0. $$

Step 3 We solve the equations.

syms lam
[lsol,xsol, ysol, zsol] = solve(gradT(1)-lam*gradg(1),gradT(2)-lam*gradg(2),gradT(3)-lam*gradg(3),g);
[xsol,ysol,zsol,lsol]

 
ans =
 
[    0,    4,        0,        0]
[  4/3, -4/3,     -4/3,        2]
[ -4/3, -4/3,     -4/3,        2]
[    0,   -2,  3^(1/2), -3^(1/2)]
[    0,   -2, -3^(1/2),  3^(1/2)]

Step 4 Plug the resulting values for (x,y,z) into T and look to see where the maximum occurs. First we turn T into a function

Tfun = inline(vectorize(T))
double([xsol,ysol,zsol, Tfun(xsol,ysol,zsol)])

Tfun =

     Inline function:
     Tfun(x,y,z) = 8.*x.^2 - 16.*z + 4.*y.*z + 600


ans =

         0    4.0000         0  600.0000
    1.3333   -1.3333   -1.3333  642.6667
   -1.3333   -1.3333   -1.3333  642.6667
         0   -2.0000    1.7321  558.4308
         0   -2.0000   -1.7321  641.5692

The hottest points on the probe's surface are

$$\left(\pm \frac 4 3 , \,\mbox{--}\,\frac 4 3 ,\,\mbox{--}\,\frac 4 3 \right).$$


Published with MATLAB® 7.9