A Surface of Revolution

syms x t

I will revolve the curve

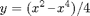
$y=(x^2\,\mbox{--}\,x^4)/4$

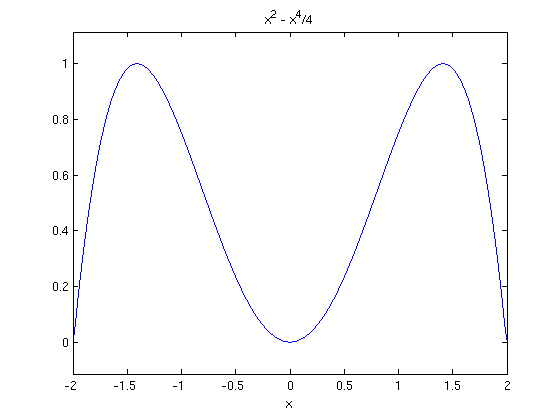
about the x-axis. Here is a plot of the curve.

ezplot((4*x^2-x^4)/4,[-2,2])

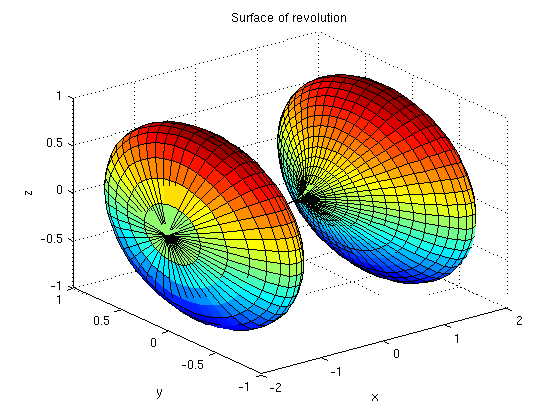
Here is a plot of the surface of revolution. The ezsurf command assumes the variables are ordered alphabetically (at least in simple examples) when figuring out the domain of each variable, so I have to list the t interval before the x interval.

ezsurf(x,(4*x^2-x^4)*cos(t)/4,(4*x^2-x^4)*sin(t)/4,[0,2*pi,-2,2])
title('Surface of revolution')

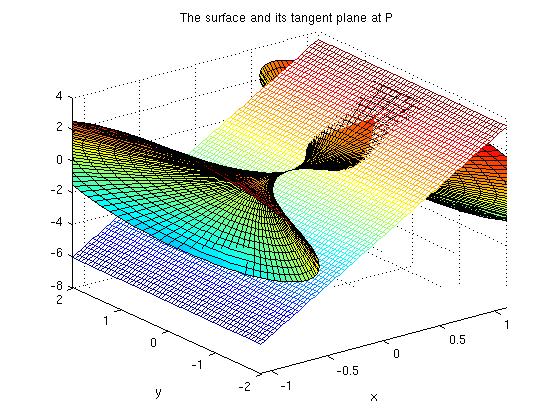
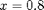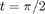Now I want to plot the surface along with its tangent plane at the point where $x=0.8$ and $t = \pi/2$ . I begin by finding the equation of the tangent plane.

clear all
syms x y z t
f = [x,(4*x^2-x^4)*cos(t),(4*x^2-x^4)*sin(t)];
fx = diff(f,x);
ft = diff(f,t);
P = subs(f,[x,t],[.8,pi/2]);
fxp = subs(fx,[x,t],[.8,pi/2]);
ftp = subs(ft,[x,t],[.8,pi/2]);
normal =cross(fxp,ftp);
planeeqn = normal *transpose([x,y,z]-P)

 
planeeqn =
 
(5268390107451449*x)/562949953421312 - (5341332971543129*y)/40564819207303340847894502572032 - (1344*z)/625 - 1840016360033032132833662946123918769146279357177053141354594515883311/642775217703596110216784836936465041008881197513117134120550400000000

The equation of the tangent plane is planeeqn=0. I'll solve that for z.

planefun = solve(planeeqn,z)

 
planefun =
 
(3292743817157155625*x)/756604737398243328 - (3338333107214455625*y)/54519117014615690099570211456811008 - 262859480004718876119094706589131252735182765311007591622084930840473/197460546878544725058596301906882060597928303876029583601833082880000

So the tangent plane is the graph of planefun. To plot the surface and the tangent plane, I'll have to use surf or mesh for at least one of those, rather than an ez command. I'll use surf for the surface. Since I'll have to enter the parametrized equation in notation MATLAB understands for vectors and matrices, I'll first give the vectorize command (which tells me where to put the periods).

vectorize(f)

ans =

matrix([[x, cos(t).*(4.*x.^2 - x.^4), sin(t).*(4.*x.^2 - x.^4)]])

Since x,t are symbolic variables, I'll use u,v as the variables for the surface. Here is the graph of the surface, along with the tangent plane. I didn't give the axis equal command, so things aren't to scale. If you run the Mfile, you'll be able to rotate the plot to get a good view.

[u,v]=meshgrid(-1:.05:1,0:.02*pi:2*pi);
surf(u,(4.*u.^2-u.^4).*cos(v),(4.*u.^2-u.^4).*sin(v)), hold on
ezmesh(planefun,[-1.1,1.1,-2,2]), hold off
title('The surface and its tangent plane at P')