Calculus III Review Problems

Nancy K. Stanton

Problem 1
Problem 2
Problem 3
Problem 4
Problem 5
Problem 6
Selected Answers

The following problems are designed to review the entire course.  Good luck!!

syms x y z t p

Problem 1

Consider the lines L1 and L2, with equations L1: (x-3)/2 = -2(y+4) = (z+1)/5 and L2: (x-6)/2 = -2(y-1) = (z-3)/5.

(a) Show that the lines are parallel.

(b) Find the equation of the plane containing the two lines.

Problem 2

A curve in space is defined by the parametrization

curve = [(3-cos(4*t))*cos(t),(3-cos(4*t))*sin(t),sin(4*t)];

Plot the curve in space and examine it from various viewpoints. (The command view([-90, -60]) makes it look like a fish!) Compute the curvature function, and plot it as a function of t. What does the graph of the curvature function tell you about the curve, and how does this mesh with the pictures?

Problem 3

Consider the surface whose equation is

surfeq = 'x^(2/3)+y^(2/3)+z^(2/3)=1';

a) Draw a picture of the surface. (Note: fractional exponents sometimes cause problems in MATLAB and other similar software packages, because they are evaluated as complex numbers. You can get around this problem by using real in any graphing command.)

(b) What special features do you observe? At what points on the surface is there no well-defined tangent plane?

P = [sym('sqrt(3)/9'), sym('sqrt(3)/9'), sym('sqrt(3)/9')];

lies on the surface and find the tangent plane to the surface at this point.

(d) Make a suitable change of variables to compute (exactly!) the volume enclosed by the surface. (Hint: if you let x=u^3, y=v^3, z=w^3, what happens to the equation? Now make a further change of variables well adapted to the situation.)

(e) Check your answer to (d) by comparing with a numerical triple integral in Cartesian coordinates, computed with numint3.

Problem 4

Let S be the portion of the hyperboloid with equation x^2 + y^2 - z^2 = 4 between z = -2 and z = 2.

(a) Parametrize the hyperboloid and plot it.

(b) Find the flux of the vector field F = [x^3, y^3, 0] through S.

(c) Compute the divergence of F and integrate it over the solid region where x^2 + y^2 - z^2 < 4 and -2 < z < 2. Relate the answer to the answer from (b) using the Divergence Theorem. Caution: S is not closed!

Problem 5

Find the real critical points of the function

h = x^3 + y^3 - z^3 - x*y*z + x - 10*y^2

 
h =
 
x^3 - x*y*z + x + y^3 - 10*y^2 - z^3

and then find the maximum and minimum values of h on the ball 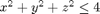$x^2 + y^2 + z^2 \le 4$ .

Problem 6

Let C be the oriented closed curve in the first octant consisting of three circular arcs: the portion of (x^2 + y^2 = 1, z = 0) from (1,0,0) to (0,1,0), followed by the portion of (y^2 + z^2 = 1, x = 0) from (0,1,0) to (0,0,1), followed by the portion of (x^2 + z^2 = 1, y = 0) from (0,0,1) to (1,0,0). Let

G = [y^2, z^2, x^2];

and compute the integral along C of G.d r, both directly and using Stokes' Theorem.

Selected Answers

1. a) Both lines point in the direction of the vector (2, -1/2, 5), hence they are parallel.

b) The equation is 54x-14y-23z=241.

c) 5.5785.

3. a) The best way to do this is with

ezsurf(cos(t)^3*sin(p)^3,sin(t)^3*sin(p)^3,cos(p)^3,[0,pi,0,2*pi])

b) There are 6 cusps and 8 "fold lines" where the surface intersects the coordinate planes. On the fold lines the tangent plane is not well defined.

d) Use the parametrization above to compute that the answer is 4*pi/35.

5. There are only two real critical points: (-0.0101, 6.6666, 0.1500) and (-2.0411, 6.4456, 2.0941). Both are outside the ball. So the maximum and minimum of the function occur on the sphere x^2 + y^2 + z^2 = 4. One can either use Lagrange multipliers (eliminate lambda and solve the equations diff(h,x)*y=diff(h,y)*x, diff(h,x)*z =diff(h,z)*x) or else parametrize the sphere with spherical coordinates and thereby reduce to a function of two variables. The maximum value subject to the constraint is 10 at (2,0,0), and the minimum value is -48.0194 at (-0.0389, -1.9996, 0.0030).

6. Solution using Stokes' Theorem: Choose S to be the portion of the unit sphere in the first octant. Then n = [x,y,z] on S and the line integral over C of G.d r is equal to the surface integral over S of curl G.n dS. We compute this as follows:

pt=[x,y,z]; curlG=curl(G,pt);
realdot = @(u, v) u*transpose(v);
integrand=realdot(curlG,pt)
sphere=[cos(t)*sin(p),sin(t)*sin(p),cos(p)]
integrandspherical=subs(integrand,pt,sphere)
flux=symint2(integrandspherical*sin(p),p,0,pi/2,t,0,pi/2)

 
integrand =
 
- 2*x*y - 2*x*z - 2*y*z
 
 
sphere =
 
[ cos(t)*sin(p), sin(p)*sin(t), cos(p)]
 
 
integrandspherical =
 
- 2*cos(t)*sin(p)^2*sin(t) - 2*cos(p)*cos(t)*sin(p) - 2*cos(p)*sin(p)*sin(t)
 
 
flux =
 
-2

Direct calculation: let

C1=[cos(t),sin(t),0];C2=[0,cos(t),sin(t)];C3=[sin(t),0,cos(t)];

Then the line integral splits into three pieces and becomes:

GC1=subs(G,pt,C1); GC2=subs(G,pt,C2); GC3=subs(G,pt,C3);
int(realdot(GC1,diff(C1)),t,0,pi/2) + int(realdot(GC2,diff(C2)),t,0,pi/2) + int(realdot(GC3,diff(C3)),t,0,pi/2)

 
ans =
 
-2