Surface Integrals, Stokes' Theorem and the Divergence Theorem

Nancy K. Stanton

based on original versions © 2000-2005 by Paul Green and Jonathan Rosenberg, modified with permission

Contents

Surface Area and Surface Integrals

We begin this lesson by studying integrals over parametrized surfaces. Recall that a surface is an object in 3-dimensional space that locally looks like a plane. In other words, the surface is given by a vector-valued function r (encoding the x, y, and z coordinates of points on the surface) depending on two parameters, say u and v. The key idea behind all the computations is summarized in the formula

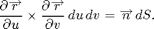
$$ \frac{\partial\overrightarrow r}{\partial u} \times \frac{\partial\overrightarrow r}{\partial v} \,du\,dv = \overrightarrow n\, dS. $$

Since r is vector-valued,

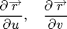
$$\frac{\partial\overrightarrow r}{\partial u}, \quad \frac{\partial\overrightarrow r}{\partial v}$$

are vectors, and their cross-product is a vector with two important properties: it is normal to the surface parametrized by r, and its length gives the scale factor between area in the parameter space and the corresponding area on the surface. Thus, taking lengths on both sides of the above formula above gives

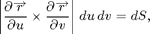
$$ \left|\frac{\partial\overrightarrow r}{\partial u} \times \frac{\partial\overrightarrow r}{\partial v} \right| \,du\,dv = dS,$$

which enables us to compute the area of a parametrized surface, or to integrate any function along the surface with respect to surface area.

Example 1

To see how this works, let us compute the surface area of the ellipsoid whose equation is

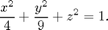
$$ \frac{x^2}{4} + \frac{y^2}{9} + z^2 = 1. $$

We may parametrize this ellipsoid as we have done in the past, using modified spherical coordinates:

syms x y z p t
ellipsoid=[2*sin(p)*cos(t),3*sin(p)*sin(t),cos(p)]

 
ellipsoid =
 
[ 2*cos(t)*sin(p), 3*sin(p)*sin(t), cos(p)]

To check that this really is a parametrization, we verify the original equation:

simplify(subs((x^2/4)+(y^2/9)+z^2,[x,y,z],ellipsoid))

 
ans =
 
1

And we can also draw a picture with ezsurf:

ezsurf(ellipsoid(1),ellipsoid(2),ellipsoid(3),[0,pi,0,2*pi])

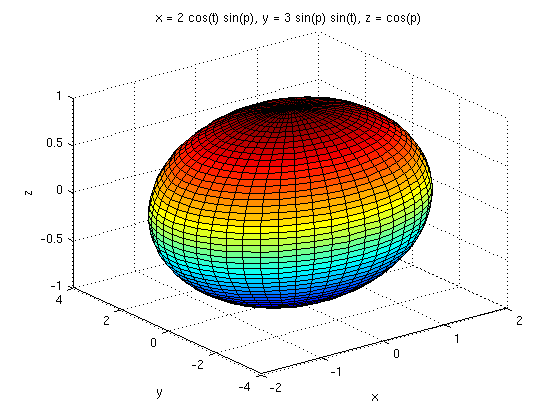
This is as it should be. Now we compute the surface area factor:

realdot = @(u,v) u*transpose(v);
veclength = @(u) sqrt(realdot(u,u));
surffactor = simple(veclength(cross(diff(ellipsoid,t), ...
    diff(ellipsoid,p))))

 
surffactor =
 
(- 5*sin(p)^4*sin(t)^2 - 27*sin(p)^4 + 36*sin(p)^2)^(1/2)

This is going to be too complicated to integrate symbolically, so we do a numerical integration, using newnumint2 from the numerical integration toolbox nit, which is a folder in the mfiles you downloaded on Assignment 1. Make sure it is in your path.

area=newnumint2(surffactor,p,0,pi,t,0,2*pi)

area =

   48.8822

To integrate a function, such as

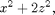
$$x^2 + 2z^2, $$

over the surface, we must express it in terms of the parameters and insert the result as a factor in the integrand.

func=subs(x^2+2*z^2,[x,y,z],ellipsoid)
integral=newnumint2(surffactor*func,p,0,pi,t,0,2*pi)

 
func =
 
2*cos(p)^2 + 4*cos(t)^2*sin(p)^2
 

integral =

  100.5002

Example 2

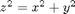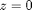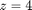Here's another example: suppose we want the surface area of the portion of the cone $z^2 = x^2 + y^2$ between $z = 0$ and $z = 4$. In cylindrical coordinates the equation of the portion of the cone with 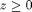$z \ge 0$ is just $z = r$, so we can take as our parameters r and t (representing theta).

syms r; cone=[r*cos(t),r*sin(t),r]

 
cone =
 
[ r*cos(t), r*sin(t), r]

The picture is:

ezsurf(cone(1),cone(2),cone(3),[0,4,0,2*pi])
conesurffactor=simple(veclength(cross(diff(cone,r),diff(cone,t)) ))

 
conesurffactor =
 
(2*r^2)^(1/2)

The surface area is

conesurf=symint2(2^(1/2)*r,r,0,4,t,0,2*pi)

 
conesurf =
 
16*pi*2^(1/2)

This is right since we can also "unwrap" the cone to a sector of a circular disk, with radius 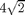$4\sqrt 2$ and outer circumference 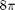$8\pi$ (compared to 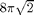$8\pi\sqrt 2$ for the whole circle), so the surface area is

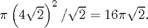
$$ \pi \left(4 \sqrt{2}\right)^2 / \sqrt{2} = 16\pi\sqrt{2}. $$

Problem 1

(a) Compute the surface area of the portion of the paraboloid 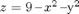$z = 9 \,\mbox{--}\, x^2 \,\mbox{--}\mbox y^2$ that lies above the 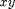$xy$-plane.

(b) Evaluate

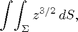
$$ \int\!\int_\Sigma z^{3/2}\,dS, $$

where 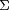$\Sigma$ is the surface whose area you found in part (a).

Flux Integrals

The formula

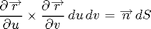
$$ \frac{\partial\overrightarrow r}{\partial u} \times \frac{\partial\overrightarrow r}{\partial v} \,du\,dv = \overrightarrow n\, dS $$

also allows us to compute flux integrals over parametrized surfaces.

Example 3

Let us compute

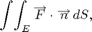
$$\int\!\int_E \overrightarrow F \cdot \overrightarrow n\,dS,$$

where the integral is taken over the ellipsoid E of Example 1, F is the vector field defined by the following input line, and n is the outward normal to the ellipsoid.

F = [x,y,z]
ndS = cross(diff(ellipsoid,p),diff(ellipsoid,t))

 
F =
 
[ x, y, z]
 
 
ndS =
 
[ 3*cos(t)*sin(p)^2, 2*sin(p)^2*sin(t), 6*cos(p)*sin(p)*cos(t)^2 + 6*cos(p)*sin(p)*sin(t)^2]

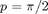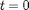We can check that we have the outward normal by setting $p=\pi/2$ and $t=0$, giving us the point of the ellipsoid that is on the positive x-axis. The outward normal should point in the positive x direction.

subs(ndS,[p,t],[pi/2,0])

ans =

    3.0000         0    0.0000

Before we can evaluate the integral, we must evaluate F in terms of the parameters.

Fpar = subs(F,[x,y,z],ellipsoid)
flux = symint2(realdot(Fpar,ndS),p,0,pi,t,0,2*pi)

 
Fpar =
 
[ 2*cos(t)*sin(p), 3*sin(p)*sin(t), cos(p)]
 
 
flux =
 
24*pi

Problem 2

Evaluate

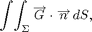
$$\int\!\int_\Sigma \overrightarrow G \cdot \overrightarrow n\,dS, $$

where 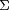$\Sigma$ is the surface of Problem 1 and G is defined by the input line below.

G=[2*x,y,z-2]

 
G =
 
[ 2*x, y, z - 2]

Stokes' Theorem

Stokes' Theorem states that if S is an oriented surface with boundary curve C, and F is a vector field differentiable throughout S, then

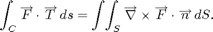
$$ \int_C\overrightarrow F \cdot \overrightarrow T\,ds = \int\!\int_S \overrightarrow\nabla \times \overrightarrow F\cdot \overrightarrow n\,dS. $$

where C is positively oriented.

Example 4

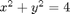Let us perform a calculation that illustrates Stokes' Theorem. We will choose S to be the portion of the hyperbolic paraboloid $z = xy$ that is contained in the cylinder $x^2 + y^2 = 4$, oriented by the upward normal n, and we will take F4 as defined below.

syms z
F4 = [z,x,y]

 
F4 =
 
[ z, x, y]

We can parametrize S conveniently using polar coordinates.

syms r
sigma = [r*cos(t),r*sin(t),r^2*cos(t)*sin(t)]

 
sigma =
 
[ r*cos(t), r*sin(t), r^2*cos(t)*sin(t)]

This has the great advantage that we can parametrize the boundary curve by setting r to 2.

boundary=subs(sigma,r,2)

 
boundary =
 
[ 2*cos(t), 2*sin(t), 4*cos(t)*sin(t)]

Let us now evaluate both sides of Stokes' theorem in this case.

int(realdot(subs(F4,[x,y,z],boundary),diff(boundary,t)),t,0,2*pi)
ndS=simplify(cross(diff(sigma,r),diff(sigma,t)))
curlF4=curl(F4,[x,y,z])
symint2(realdot(curlF4,ndS),r,0,2,t,0,2*pi)

 
ans =
 
4*pi
 
 
ndS =
 
[ -r^2*sin(t), -r^2*cos(t), r]
 
 
curlF4 =
 
[ 1, 1, 1]
 
 
ans =
 
4*pi

Problem 3

Verify Stokes' theorem for the case in which S is the portion of the upper sheet of the hyperbolic paraboloid

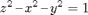
$$ z^2 \,\mbox{--}\,x^2\,\mbox{--}\, y^2 = 1 $$

that lies below the plane 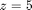$z = 5$, and F5 is the following input cell.

F5=[-z*y,z*x,x^2+y^2]

 
F5 =
 
[ -y*z, x*z, x^2 + y^2]

The Connection with Area

As in the case of Green's Theorem, if F is a vector field such that 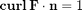$\mbox{\textbf{curl}}\,\mathbf{F} \cdot \mathbf{n} = 1$ on a surface S with boundary curve C, then Stokes' Theorem says that

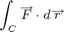
$$ \int_C\overrightarrow F\cdot d\overrightarrow r $$

computes the surface area of S.

Problem 4

Let S be the spherical cap 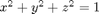$x^2 + y^2 + z^2 = 1$, with 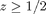$z \ge 1/2$, so that the bounding curve of S is the circle 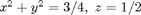$x^2 + y^2 = 3/4,\ z = 1/2$. Show that if

F6=[0,atan(x/sqrt(1-x^2-y^2)),0]

 
F6 =
 
[ 0, atan(x/(- x^2 - y^2 + 1)^(1/2)), 0]

then curl F6 . n = 1 on S, and confirm that

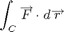
$$ \int_C \overrightarrow F\cdot d\overrightarrow r $$

is equal to the surface area of S, which you can compute independently in spherical coordinates.

The Divergence Theorem

Example 5

The Divergence Theorem says that we can also evaluate the integral in Example 3 by integrating the divergence of the vector field F over the solid region bounded by the ellipsoid. But one caution: the Divergence Theorem only applies to closed surfaces. That's OK here since the ellipsoid is such a surface. The div command, which computes the divergence of a vector field, is one of the M-files you downloaded. Although computing the divergence of F is very easy in the present case, we illustrate the syntax of div:

divF = div(F,[x,y,z])

 
divF =
 
3

We must now parametrize the solid ellipsoid. We can do this most easily by adding a radial factor r that takes values between 0 and 1. Note that since ellipsoid is a vector, all we have to do is "scalar multiply" it by r:

syms r
solid = r*ellipsoid

 
solid =
 
[ 2*r*cos(t)*sin(p), 3*r*sin(p)*sin(t), r*cos(p)]

Recall that to integrate in the coordinates r, p, and t, we are going to have to insert a scale factor, the absolute value of the determinant of the Jacobian matrix of the change of variables. As we indicated in the MATLAB lesson on change of variables, it's usually easiest to leave off the absolute value at first, and then change the sign if the scale factor comes out negative.

scale=simple(det(jacobian(solid,[r,p,t])))

 
scale =
 
6*r^2*sin(p)

That's clearly positive, and it's simple enough to make a symbolic integration feasible.

answer = int(symint2(3*scale,r,0,1,p,0,pi),t,0,2*pi)

 
answer =
 
24*pi

This agrees with our calculation of the flux. The numerical value is:

double(24*pi)

ans =

   75.3982

Problem 5

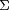With G and $\Sigma$ as in Problems 1 and 2, integrate the divergence of G over the solid region bounded above by $\Sigma$ and below by the 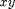$xy$-plane. Why is your answer not the same as the answer to Problem 2?

Additional Problems

1. Check the accuracy of the computation in Example 1 above by repeating the integration over the ellipsoid, using x and y as the parameters and solving for z as a function of x and y. (Hint: since there are two solutions for z, but the surface is symmetric, just integrate over the top half of the ellipsoid and then double the result.)

2. Let

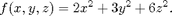
$$ f(x,y,z) = 2x^2 + 3y^2 +6z^2 . $$

Compute the flux of the gradient of f through the ellipsoid

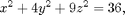
$$ x^2 + 4y^2 + 9z^2 = 36, $$

both directly and by using the Divergence Theorem.

3. Let T be the torus with equation 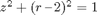$z^2 + (r\,\mbox{--}\,2)^2 = 1$ in cylindrical coordinates. Parametrize the torus and use the answer to compute the surface area.

4. Let T be the same torus as in Additional Problem 3 just above. Compute the volume enclosed by the torus two ways: by triple integration, and by computing the flux of the vector field F = (x,y,z) through T and using the Divergence Theorem. Check that the results agree, and also that they agree with the result obtained by using the Theorem of Pappus (see Stewart, section 9.3): the volume of a solid obtained by rotating a region R in the xz-plane around the z-axis is the area of R times the circumference of the circle traced out by the center of mass of R as it rotates around the z-axis.


Published with MATLAB® 7.9