Using ode45 to solve a system of three equations

Contents

The system

Consider the nonlinear system

$$x'=-x+3z$$

$$y'=-y+2z$$

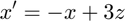
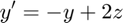
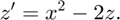
$$z'=x^2-2z.$$

dsolve can't solve this system. I need to use ode45 so I have to specify an initial value

Solution using ode45.

This is the three dimensional analogue of Section 14.3.3 in Differential Equations with MATLAB. Think of 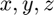$x,y,z$ as the coordinates of a vector x. In MATLAB its coordinates are x(1),x(2),x(3) so I can write the right side of the system as a MATLAB function

f = @(t,x) [-x(1)+3*x(3);-x(2)+2*x(3);x(1)^2-2*x(3)];

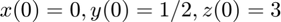The numerical solution on the interval $[0,1.5]$ with $x(0)=0,y(0)=1/2,z(0)=3$ is

[t,xa] = ode45(f,[0 1.5],[0 1/2 3]);

Plotting components

I can plot the components using plot. For example, to plot the graph of 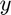$y$ I give the command:

plot(t,xa(:,2))
title('y(t)')
xlabel('t'), ylabel('y')

3 D plot

I can plot the solution curve 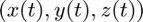$(x(t),y(t),z(t))$ in phase space using plot3.

plot3(xa(:,1),xa(:,2),xa(:,3))
grid on
title('Solution curve')

Using ode45 on a system with a parameter.

Suppose I change the system to

$$x'=-x+az$$

$$y'=-y+2z$$

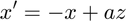
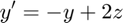
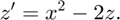
$$z'=x^2-2z.$$

and I would like to use a loop to solve and plot the solution for 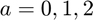$a=0,1,2$.

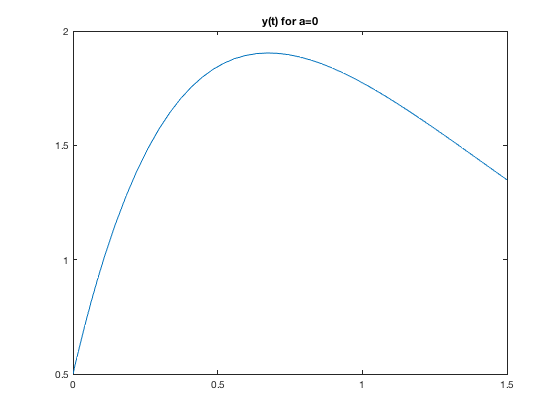
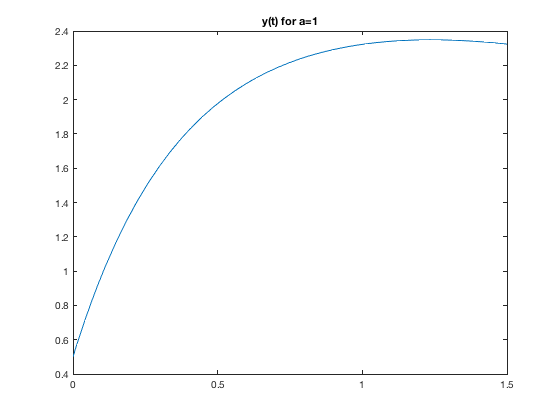
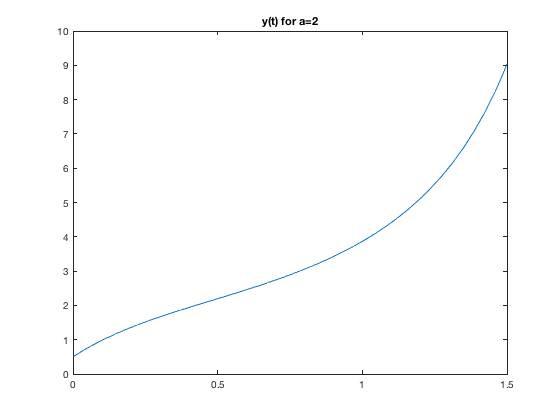
syms t x a
g = @(t,x,a)[-x(1)+a*x(3);-x(2)+2*x(3);x(1)^2-2*x(3)]
for a = 0:2
[t,xa] = ode45(@(t,x) g(t,x,a),[0 1.5],[1 1/2 3]);
figure
plot(t,xa(:,2))
title(['y(t) for a=',num2str(a)'])
end

g =

  function_handle with value:

    @(t,x,a)[-x(1)+a*x(3);-x(2)+2*x(3);x(1)^2-2*x(3)]


Published with MATLAB® R2017b