DIFFERENTIAL EQUATIONS WITH MATLAB

CHAPTER 5

An illustration of stability

We look at how the solution to

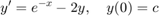
$y' = e^{-x} - 2y,\quad y(0)=c$

depends on the initial value c.

syms x
eqn = 'Dy = exp(-x) - 2*y'
Y = dsolve(eqn, 'y(0) = c', 'x')

eqn =

Dy = exp(-x) - 2*y

 
Y =
 
exp(-x) + exp(-2*x)*(c - 1)

We plot the solution for initial values .9, 1 and 1.1.

figure;
hold on
for j = -1:1
    ezplot(subs(Y,'c',1 + j/10),[-1,1])
end
axis tight
hold off
title('Solutions of dy/dx=e^{-x}-2y')

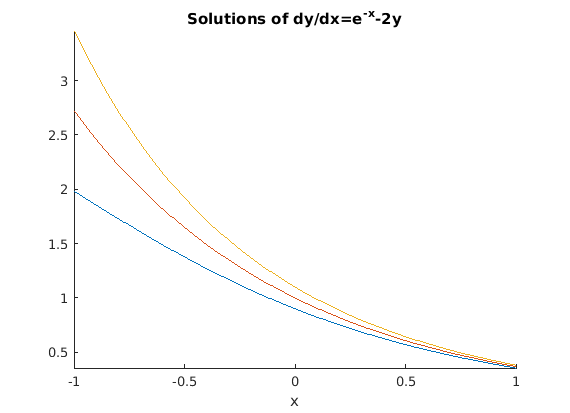
The inital values are close together. (Two consecutive functions have values which differ by 0.1.) The plots remain close together for positive x, and in fact become closer together. This equation is stable. The derivative of the right side with respect to y is negative.

An illustration of instability

Now we look at the same question for the equation

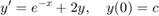
$y' = e^{-x} + 2y,\quad y(0) = c$

eqn2 = 'Dy = exp(-x) + 2*y'
Y_2 = dsolve(eqn2,'y(0)=c','x')

eqn2 =

Dy = exp(-x) + 2*y

 
Y_2 =
 
exp(2*x)*(c + 1/3) - exp(-x)/3

We plot the solution for inital values -11/30, -10/30 and -9/30.

figure;
hold on
for j = -1:1
    ezplot(subs(Y_2,'c',-1/3 + j/30),[-1,1])
end
axis tight
hold off
title('Solutions of dy/dx=e^{-x}+2y')

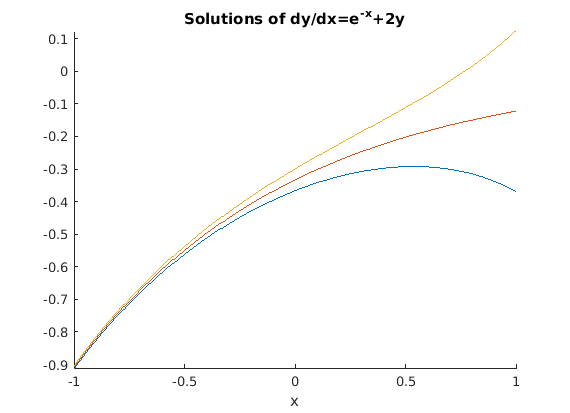
The functions have initial values at x=0 which are close together. (Two consecutive functions have initial values which differ by 1/30). However, the plots spread apart for positve x. This equation is unstable. The derivative of the right side with respect to y is positive.