Using dsolve to solve first order ODEs

Contents

Section 2.2 #9

Solve 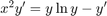$x^2y'=y \ln y - y'$.

I solve it using dsolve. The equation has to be enclosed in single quotes and so does the independent variable. (If you leave out the argument for the independent variable, MATLAB assumes it is $t$, which isn't what you want here!)

syms x
dsolve('x^2*Dy = y*log(y) - Dy','x')

 
ans =
 
                      1
 exp(exp(C5 + atan(x)))

You could also define the equation in MATLAB and give it a name, then use that in dsolve.

eqn = 'x^2*Dy = y*log(y) - Dy'
dsolve(eqn,'x')

eqn =

x^2*Dy = y*log(y) - Dy

 
ans =
 
                      1
 exp(exp(C5 + atan(x)))

Solving an inital value problem

Solve the same problem with 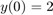$y(0)=2$.

I add the initial value as the second argument. The independent variable has to be the last argument.

dsolve('x^2*Dy = y*log(y) - Dy','y(0)=2','x')

 
ans =
 
exp(exp(log(log(2)) + atan(x)))

I could also combine the equation and initial value into one argument.

dsolve('x^2*Dy = y*log(y) - Dy, y(0)=2','x')

 
ans =
 
exp(exp(log(log(2)) + atan(x)))

Solving with a general initial value 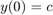$y(0)=c$

Y= dsolve('x^2*Dy = y*log(y) - Dy','y(0)=c','x')

 
Y =
 
exp(exp(log(log(c)) + atan(x)))

This is messy. I'll simplify it.

Y = simplify(Y)

 
Y =
 
exp(exp(atan(x))*log(c))

That helps a little.

You could define the initial value problem in MATLAB, give it a name and use it in dsolve.

IVP = 'x^2*Dy = y*log(y) - Dy, y(0)=c'
dsolve(IVP,'x')

IVP =

x^2*Dy = y*log(y) - Dy, y(0)=c

 
ans =
 
exp(exp(log(log(c)) + atan(x)))

Plotting the solutions for several initial values

Plot the solutions with initial values 0,1,2,3,4

figure;
hold on
for j = 0:4
    ezplot(subs(Y,'c',j),[0 1])
end
hold off
axis([0 1 -1 25])
title('Solutions with initial value 0,...,4')

The examples in Differential Equations with MATLAB use the figure command. At least here you can omit it.


Published with MATLAB® R2015b