SECTION 6.1 - EULER'S METHOD
Here I use the function myeuler (from pages 104-105 of Differential Equations with MATLAB) implementing Euler's method to solve y' = 2y - 1. It takes as input the function f, the initial time tinit, the initial y-value yinit, the final time value b and the number of steps n.
syms t y f = @(t,y) 2*y - 1
f =
@(t,y)2*y-1
First I use step size 0.1.
[t1,y1] = myeuler(f,0,1,0.4,4); [t1,y1]
ans =
0 1.0000
0.1000 1.1000
0.2000 1.2200
0.3000 1.3640
0.4000 1.5368
Next I use step size 0.05.
[t2,y2] = myeuler(f,0,1,0.4,8); [t2,y2]
ans =
0 1.0000
0.0500 1.0500
0.1000 1.1050
0.1500 1.1655
0.2000 1.2321
0.2500 1.3053
0.3000 1.3858
0.3500 1.4744
0.4000 1.5718
Finally I use step size 0.025
[t3,y3] = myeuler(f,0,1,0.4,16); [t3,y3]
ans =
0 1.0000
0.0250 1.0250
0.0500 1.0513
0.0750 1.0788
0.1000 1.1078
0.1250 1.1381
0.1500 1.1700
0.1750 1.2036
0.2000 1.2387
0.2250 1.2757
0.2500 1.3144
0.2750 1.3552
0.3000 1.3979
0.3250 1.4428
0.3500 1.4900
0.3750 1.5395
0.4000 1.5914
The exact solution is
y = dsolve('Dy = 2*y-1, y(0) = 1','t')
y = exp(2*t)/2 + 1/2
Here is a table of values. The first entry is t, followed by the approximate solutions evaluated at that value of t, followed by the exact solution evaluated at that value of t. I build the table T a row at a time using a for loop. I initialize T with an empty row.
format short T = [ ]; for k=0:4 A = [t1(k+1),y1(k+1),y2(2*k+1),y3(4*k+1),subs(y,'t',t1(k+1))]; T = [T;A]; end T
T = [ 0, 1, 1, 1, 1] [ 1/10, 11/10, 221/200, 2494438280484251/2251799813685248, exp(1/5)/2 + 1/2] [ 1/5, 61/50, 24641/20000, 2789366853368857/2251799813685248, exp(2/5)/2 + 1/2] [ 3/10, 341/250, 1560250135854325/1125899906842624, 6295708754027351/4503599627370496, exp(3/5)/2 + 1/2] [ 2/5, 1921/1250, 7078732696661031/4503599627370496, 3583598202550975/2251799813685248, exp(4/5)/2 + 1/2]
I use double to convert the entries to decimals.
double(T)
ans =
0 1.0000 1.0000 1.0000 1.0000
0.1000 1.1000 1.1050 1.1078 1.1107
0.2000 1.2200 1.2321 1.2387 1.2459
0.3000 1.3640 1.3858 1.3979 1.4111
0.4000 1.5368 1.5718 1.5914 1.6128
I plot the three approximate solutions and the exact solution. I do two types of plots, one where I show just the points computed by Euler's method, the other where the points are connected by line segments.
plot(t1,y1,'.c','MarkerSize',15), hold on plot(t2,y2,'.r','MarkerSize',15) plot(t3,y3,'.g','MarkerSize',15) ezplot(y,[0,0.4]) title 'Solutions using Eulers method and the exact solution' legend1 = legend({'step size 0.1', 'step size 0.05', 'step size 0.025','exact'},... 'Position',[0.1465 0.7205 0.2171 0.1869]); hold off
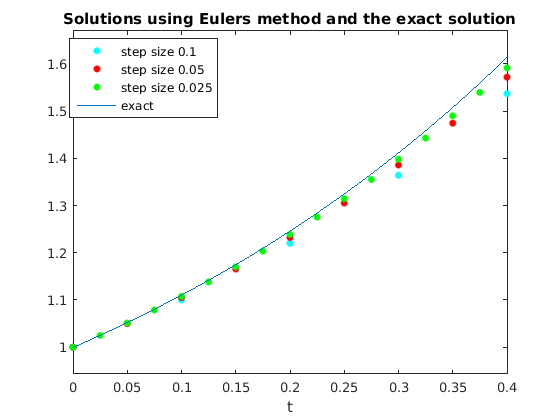
plot(t1,y1,'c'), hold on plot(t2,y2,'r') plot(t3,y3,'g') ezplot(y,[0,0.4]) title 'Solutions using Eulers method and the exact solution' legend1 = legend({'step size 0.1', 'step size 0.05', 'step size 0.025','exact'},... 'Position',[0.1465 0.7205 0.2171 0.1869]); hold off
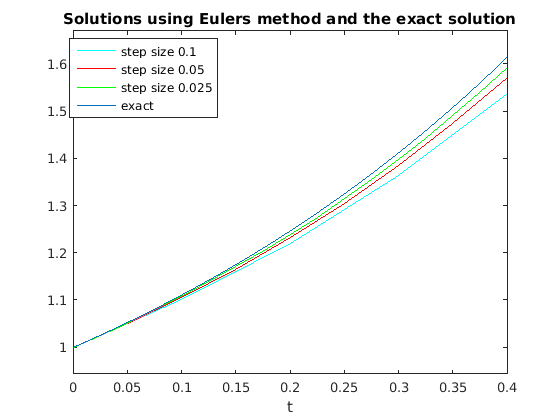
I see from both the plots and the table that the error in the approximate solutions decreases as the number of steps increases, but it is still fairly large.
I can look at the errors. Here is a table with t in the first column, y1(t) in the second, y(t) in the third and e1(t)=y(t)-y1(t) in the fourth. Using double converts the entries in the table to decimals.
format short T = [ ]; for k=0:4 A = [t1(k+1),y1(k+1),subs(y,'t',t1(k+1)),subs(y,'t',t1(k+1))-y1(k+1)]; T = [T;A]; end double(T)
ans =
0 1.0000 1.0000 0
0.1000 1.1000 1.1107 0.0107
0.2000 1.2200 1.2459 0.0259
0.3000 1.3640 1.4111 0.0471
0.4000 1.5368 1.6128 0.0760
Here is a table with t in the first column, y3(t) in the second, y(t) in the third and e1(t)=y(t)-y3(t) in the fourth. I use the same t values as in the first table of errors.
format short T = [ ]; for k=0:4 A = [t3(4*k+1),y3(4*k+1),subs(y,'t',t3(4*k+1)),subs(y,'t',t3(4*k+1))-y3(4*k+1)]; T = [T;A]; end double(T)
ans =
0 1.0000 1.0000 0
0.1000 1.1078 1.1107 0.0029
0.2000 1.2387 1.2459 0.0072
0.3000 1.3979 1.4111 0.0131
0.4000 1.5914 1.6128 0.0213
The errors are still increasing, but are much smaller than for y1.