Section 8.1 SIR model

The model is

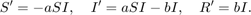
$S'=-aSI,\quad I'=aSI-bI, \quad R'=bI.$

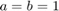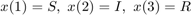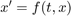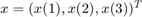If we take $a=b=1$ , we can use ode45 to solve and graph the components. Let $x(1)=S,\ x(2)=I,\ x(3)=R$ so the system becomes $x'=f(t,x)$ where $x=(x(1),x(2),x(3))^T$ and

 f = @(t,x) [-x(1)*x(2);x(1)*x(2)-x(2);x(2)]

f = 

    @(t,x)[-x(1)*x(2);x(1)*x(2)-x(2);x(2)]

We solve with 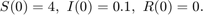$S(0)=4,\ I(0)=0.1,\ R(0)=0.$ and then plot the components of the solution.

[t,xa]=ode45(f,[0 6], [4 0.1 0]);
 plot(t,xa(:,1))
 hold on
 plot(t,xa(:,2),'k')
 plot(t,xa(:,3),'r')
 hold off

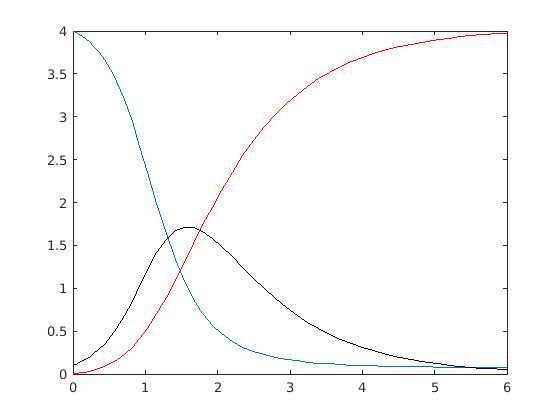
The blue curve is the population which has not yet had the disease, the black curve is the infected population and the red curve is the population which has recovered. We've now reproduced Figure 1 in Polking, Boggess and Arnold.