How to plot the tail of a solution curve

Contents

This is the same system used in the demonstration for 3 dimensional systems

Consider the nonlinear system

$$x'=-x+3z$$

$$y'=-y+2z$$

$$z'=x^2-2z.$$

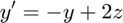
Solution using ode45.

This is the three dimensional analogue of the Section 14.3.3 in Differential Equations with MATLAB. Think of $x,y,z$ as the coordinates of a vector x. In MATLAB its coordinates are x(1),x(2),x(3) so I can write the right side of the system as a MATLAB function

f = @(t,x) [-x(1)+3*x(3);-x(2)+2*x(3);x(1)^2-2*x(3)];

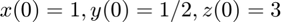The numerical solution on the interval $[0,1.5]$ with $x(0)=1,y(0)=1/2,z(0)=3$ is

[t,xa] = ode45(f,[0 1.5],[0 1/2 3]);

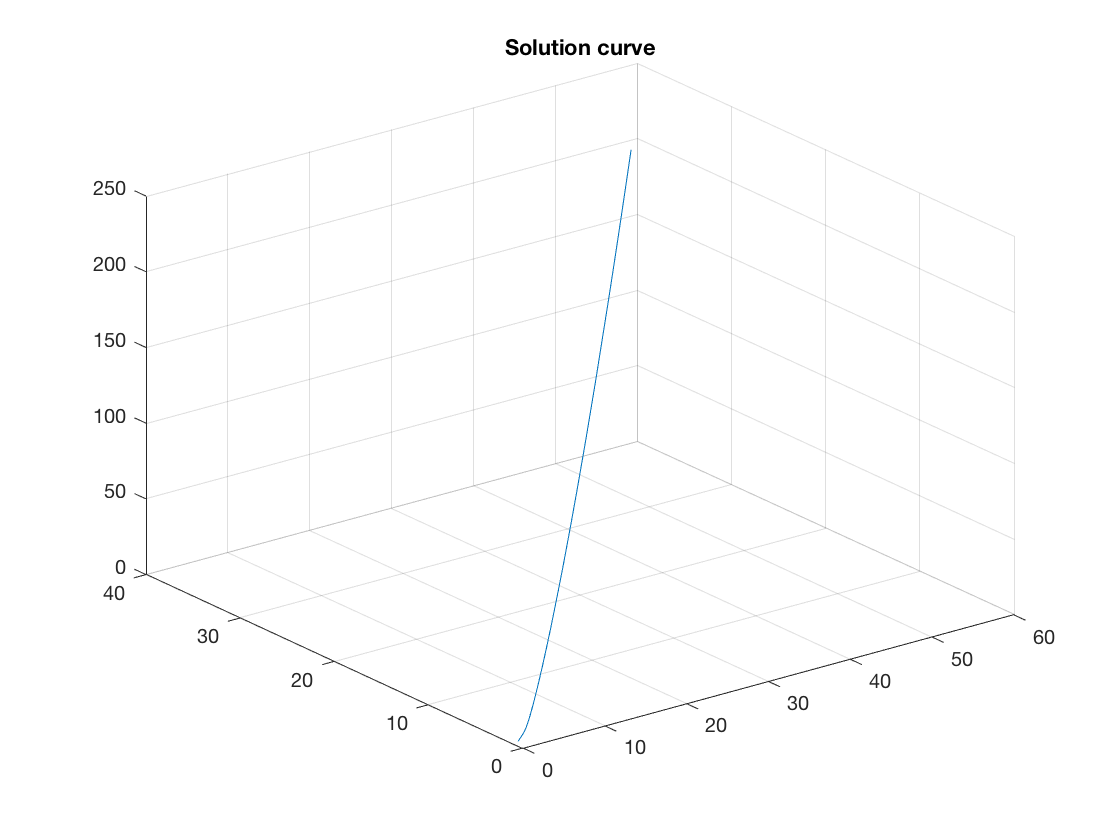
3 D plot

I can plot the solution curve 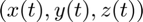$(x(t),y(t),z(t))$ in phase space using plot3.

plot3(xa(:,1),xa(:,2),xa(:,3))
grid on
title('Solution curve')

Plotting the tail

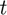Suppose I just want to plot the part which corresponds approximately to the time interval $[1,1.5]$. Remember that the $t$ produced by ode45 is a vector with a lot of components. I want to know which component corresponds approximately to 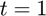$t=1$. One way is to look at the values of 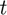$t$, but with a very long list of values this wouldn't be easy. So first I'll find how many components 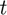$t$ has, using the command size.

size(t)

ans =

    69     1

This tells me that 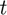$t$ has 69 rows and 1 column. Now I do some guessing: t(46) is two-thirds down the list of components of 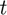$t$ so I can look at it.

t(46)

ans =

    0.8747

I look at components with slightly larger index:

t(47:50)

ans =

    0.9122
    0.9497
    0.9872
    1.0247

I see that t(49) and t(50) are the closest, one a little larger, the other a little smaller than 1. I'll use 49 as my index. (You can probably do this more elegantly using the Events option.) So I can plot the tail of the solution curve with the following command.

plot3(xa(49:69,1),xa(49:69,2),xa(49:69,3))
grid on
title('Tail of solution curve')


Published with MATLAB® R2016a