Using piecewise defined functions in MATLAB

Contents

Mathematical description

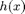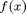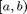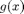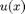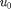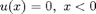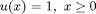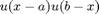Suppose $h(x)$ is equal to $f(x)$ on the interval $[a,b)$ and $g(x)$ on the interval $(b,c]$ and you want to define it as a MATLAB function. Use the unit step function or Heaviside function $u(x)$ to define the piecewise function. This is the function $u_0$ in Section 6.3 of Boyce and DiPrima. It is defined by $u(x) = 0,\ x < 0$ and $u(x)=1,\ x \ge 0$. 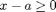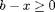Then $u(x-a)u(b-x)$ is 1 where $x-a \ge 0$ and $b-x\ge 0$, so on the interval $[a,b]$, and and it is 0 outside the interval. So

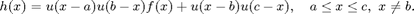
$$h(x) = u(x-a)u(b-x)f(x) + u(x-b)u(c-x), \quad a \le x \le c, \ x \ne b .$$

How can you do this in MATLAB?

The unit step function is known to MATLAB as heaviside, with the slight difference that heaviside(0)=1/2.

Example

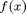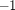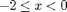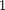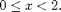Define a symbolic MATLAB function $f(x)$ which is equal to $-1$ if $-2 \le x < 0$ and is equal to $1$ if $0 \le x < 2.$ This is Boyce and DiPrima, Section 10.2 #19.

Solution:

syms x
f = -heaviside(x+2)*heaviside(-x)+heaviside(x)*heaviside(2-x)

 
f =
 
heaviside(2 - x)*heaviside(x) - heaviside(-x)*heaviside(x + 2)

Check

You can check that this is right except at the 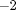$-2$ and at 0 by plotting.

ezplot(f,[-2 2])
title('graph of f')

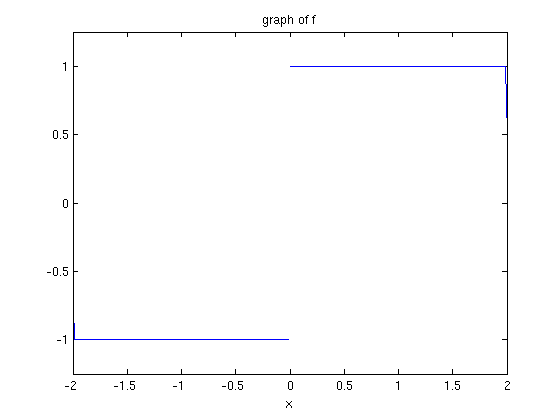
You can have MATLAB compute the values at 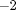$-2$ and 0.

subs(f,x,-2)

ans =

   -0.5000


subs(f,x,0)

ans =

     0

At 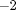$-2$ the value is $\frac 12$ and at 0 it is 0.


Published with MATLAB® 7.13