Animation of the partial sums of a Fourier Series

The command fourier_movie will let you animate the graphs of the partial sums of the Fourier series of the expression f on the interval [a,b]. f is assumed to be periodic with period L = b-a. (Notice, the period is L, not 2L). The command requires you to specify the limits on the vertical axis as well, since it creates the movie by making a frame at a time and you want the same axes for every frame. You will want to download fourier_movie.m to use it.

type fourier_movie
function fsm = fourier_movie(f,x,a,b,c,d,n)

% This animates the first n partial sums of the Fourier series of the 
% expression f on the interval [a,b].  The function is assumed to be 
% periodic with period L = b-a. The vertical axis goes from c to d. 
L = (b-a);
X = a:0.001:b;
g = inline(vectorize(f));

partsum = 1/L * double(int(f,x,a,b));
for k =1:n 
    partsum = partsum ...
        + 2/L*double(int(f*sin(2*k*pi*x/L),x,a,b))*sin(2*k*pi*x/L) ... 
        + 2/L*double(int(f*cos(2*k*pi*x/L),x,a,b))*cos(2*k*pi*x/L);
    ps2 = inline(vectorize(partsum));
    plot(X,g(X),'r'), hold on
    plot(X,ps2(X)), hold off
    axis([a b c d])
    fsm(k) = getframe;
end

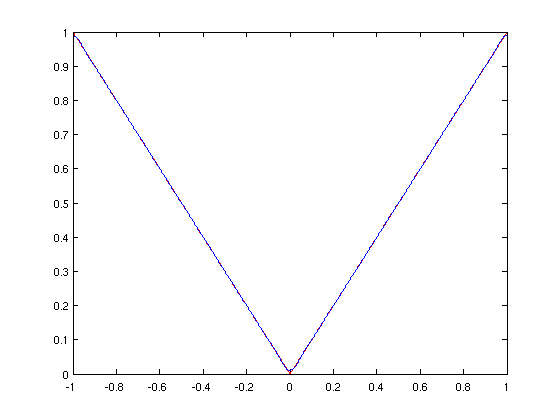
We use this with f = abs(x) on [-1,1] and take the first 20 partial sums. First we create the frames.

syms x
f = abs(x)
absx=fourier_movie(f,x,-1,1,0,1,20)
 
f =
 
abs(x)
 

absx = 

1x20 struct array with fields:

    cdata
    colormap

We can view this with mplay.

mplay(absx)

(I edited this html file to delete the output from mplay because it showed several superimposed graphs in strange ways.)

We use it with f = x on [-1,1]. Since the convergence of the series is slower for this function, we take the first 50 partial sums.

f = x
xmovie=fourier_movie(f,x,-1,1,-1.2, 1.2,50)
 
f =
 
x
 

xmovie = 

1x50 struct array with fields:

    cdata
    colormap

You can also save it as name.mat (replace "name" by the name you want) with the command save('name','mymovie') where mymovie is the name you gave the output of your fourier_movie command. The movie will then be named 'mymovie'. You can use different names for the two arguments in the save command, but when you load name.mat with the command load('name'), the movie will be named mymovie. So, for example, if I have created the movie ahead of time with the command:

save('xmovie','xmovie')

I can view it with the commands:

load('xmovie')
mplay(xmovie)

We use it with the function f = exp(x) on [0,5]. I'll take 20 partial sums.

f = exp(x)

expmovie=fourier_movie(f,x,0,5,-20,200,20)
 
f =
 
exp(x)
 

expmovie = 

1x20 struct array with fields:

    cdata
    colormap






mplay(expmovie)

Published with MATLAB® R2013a