Homework 10: Binary Heaps, Huffman Coding

The goal of this homework assignment is to allow you to explore building priority queues in Python using binary heaps and then employ these data structures in implementing a script that computes the Huffman coding for a stream of text. This encoding is a mapping from each character in the input stream to a unique bit sequence or prefix code, which unlike say ASCII is variable-length rather than fixed size. The purpose of the Huffman coding is to utilize a greedy algorithm to produce an encoding that uses less space (ie. fewer bits) than the fixed-size ASCII encoding as show below:

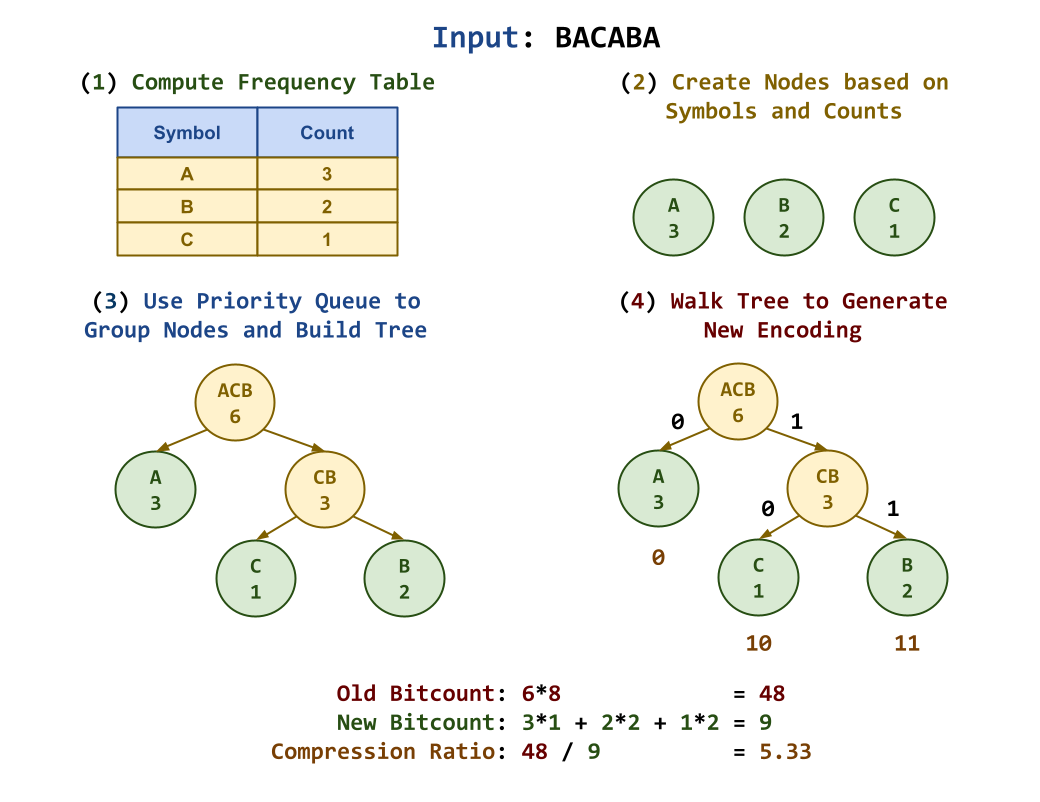
In the example above, our input sequence is: BACABA, which in ASCII would consist of a total of 48 bits (e.g. 6 bytes):

010000100100000101000011010000010100001001000001  # ASCII Representation

To generate a more compressed version of this text, we would need to construct a Huffman coding by performing the following process:

1. Compute Frequencies: First, read in the input stream and count the occurrences of each symbol (ie. character) to create a frequency table.

2. Populate Priority Queue: Next, represent each symbol and count pair as a node and push them into a priority queue.

3. Build Tree: Afterwards, construct the Huffman tree by doing the following:

   while len(queue) > 1:
       # Pop nodes with smallest counts from priority queue
       left  = queue.pop()
       right = queue.pop()
   
       # Construct new composite node
       node  = Node(left.symbol + right.symbol, left.value  + right.value, left, right)
   
       # Push new composite node into priority queue
       queue.push(node)
   
   root = queue.pop()
   

   Basically, as long there is more than one node in the priority queue, we will pop off the two smallest items, create a new node with the combined count of these two nodes, and insert this new node back into the priority queue. We repeat this process until there is only one node left in the priority queue, which we then set as the root of our Huffman tree.

   By constantly grouping nodes with the smallest counts, we use a greedy problem solving approach in order to maximize the path from the root to the nodes with the lowest occurrences (and thus minimize the path from the root to the nodes with the highest occurrences).

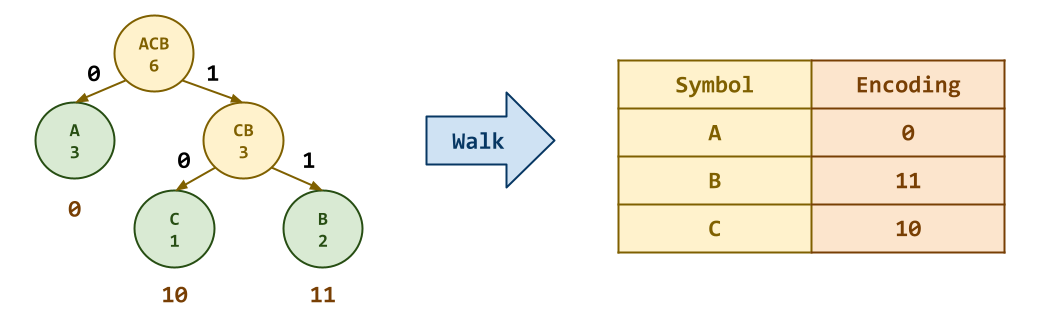
4. Walk Tree: Finally, to produce the Huffman coding, walk (ie. recursively traverse) the Huffman tree we constructed in the previous step and record the path we took to the leaf nodes (ie. the original nodes from step 2). To ensure a consistent prefix code, we can use the convention where the left child gets a 0 and the right child gets a 1 when we take the path from parent to child. In the example, above, using this traversal mechanism yields the following encoding:

   Symbol	Count	Encoding
   A	3	0
   B	2	11
   C	1	10

Using this new Huffman coding, our original text, BACABA, can be encoded as follows:

110100110     # Huffman Encoding

This means the Huffman coding was about to compress down to about 20% of the original ASCII representation. This is the reason why many real-world data compression schemes such as PKZIP, JPEG, and MP3 use elements of the Huffman coding technique to achieve smaller file sizes for different types of data.

To keep things manageable (and to respect your time), we will only worry about the construction of the Huffman coding in this assignment and leave out the actual compression and decompressing process (though you are free to implement that on your own!).

For this assignment, you are to do your work in the homework10 folder of your assignments GitHub repository and push your work by noon, Wednesday, November 15.

Activity 0: Preparation¶

Before starting this homework assignment, you should first perform a git pull to retrieve any changes in your remote GitHub repository:

$ cd path/to/repository                   # Go to assignments repository

$ git switch master                       # Make sure we are in master branch

$ git pull --rebase                       # Get any remote changes not present locally

Next, create a new branch for this assignment:

$ git checkout -b homework10              # Create homework10 branch and check it out

Task 1: Skeleton Code¶

To help you get started, the instructor has provided you with the following skeleton code:

# Go to assignments repository
$ cd path/to/assignments/repository

# -----------------------------------------------------
# MAKE SURE YOU ARE NOT INSIDE THE homework10 DIRECTORY
# -----------------------------------------------------
# MAKE SURE YOU ARE AT THE TOP-LEVEL DIRECTORY
# -----------------------------------------------------

# Download skeleton code tarball
$ curl -LO https://www3.nd.edu/~pbui/teaching/cse.20312.fa23/static/tar/homework10.tar.gz

# Extract skeleton code tarball
$ tar xzvf homework10.tar.gz

Once downloaded and extracted, you should see the following files in your homework10 directory:

homework10
    \_ Makefile           # This is the Makefile for building all the assignment artifacts
    \_ huffman.py         # This is the Python script for the Huffman coding script
    \_ node.py            # This is the Python module for the Node class and functions
    \_ priority_queue.py  # This is the Python module for the Priority Queue class and functions

Task 2: Initial Import¶

Now that the files are extracted into the homework10 folder, you can commit them to your git repository:

# Go into homework10 folder
$ cd homework10

# Add and commit initial skeleton files
$ git add Makefile                            # Mark changes for commit
$ git add *.py
$ git commit -m "Homework 10: Initial Import" # Record changes

Task 3: Unit Tests¶

After downloading and extracting these files, you can run the make command to run the tests.

# Run all tests (will trigger automatic download)
$ make

You will notice that the Makefile downloads three additional test scripts:

homework10
  \_ huffman_test.py        # This is the Python unit test for the Huffman script
  \_ node_test.py           # This is the Python unit test for the Node module
  \_ priority_queue_test.py # This is the Python unit test for the Priority Queue module

In addition to the embedded doctests in the skeleton code, you will be using these unit tests to verify the correctness and behavior of your code.

The details on what you need to implement for this assignment are described in the following sections.

Activity 1: Node (2 Points)¶

For the first activity, you are to extend and augment our usual Node dataclass:

@dataclass
class Node:
    symbol: str
    value:  int = 0
    left:   Optional['Node'] = None
    right:  Optional['Node'] = None

In particular, you will need to implement the __gt__ magic method to allow comparing two Node objects and you will need to implement the walk function that traverses a Huffman tree to construct the Huffman coding as described previously.

Task 1: node.py¶

The node.py Python script contains the Node class you are to augment and the walk function you are to complete for this activity:

1. Node.__gt__(self, other: 'Node') -> bool

   This method determines whether the current Node is greater than the other specified Node (returns True if it is greater, False otherwise). To do so, the method will first consider the value attributes as the higher priority and then consider the length of the symbol attributes as the lower priority.

2. walk(node: Optional[Node], codeword: str='') -> dict

   This function recursively traverses the binary tree starting at node and returns a dict containing a mapping of symbols to Huffman codes as shown in the diagram above.

   Hints¶

   1. When initializing a variable, you can annotate its type:

      variable: dict[str, str] = {}
      

      This will inform static type checkers such as mypy of your intentions.

   2. Use divide-and-conquer to traverse the binary tree and carefully consider your base cases (particularly when you know you have a complete codeword).

   3. Remember that the left child should add a 0 to its codeword and the right child should add a 1 to its codeword.

   4. Consider using the | operator to combine multiple dicts.

Task 2: Testing¶

As you implement node.py, you can use the provided doctests to verify the correctness of your code:

# Run doctests
$ python3 -m doctest node.py -v
...
2 items passed all tests:
   2 tests in node.Node.__gt__
   2 tests in node.walk
4 tests in 7 items.
4 passed and 0 failed.
Test passed.

You can also use make to run both the doctests and the unit tests:

# Run unit tests (and doctests)
$ make test-node
Testing node ...
test_00_doctest (__main__.NodeTests) ... ok
test_01_mypy (__main__.NodeTests) ... ok
test_02_comparison (__main__.NodeTests) ... ok
test_03_walk (__main__.NodeTests) ... ok

   Score 2.00 / 2.00
  Status Success

----------------------------------------------------------------------
Ran 4 tests in 0.048s

OK

To just run the unit tests, you can do the following:

# Run unit tests
$ ./node_test.py -v
...

To run a specific unit test, you can specify the method name:

# Run only mypy unit test
$ ./node_test.py -v NodeTests.test_01_mypy
...

Activity 2: Priority Queue (4 Points)¶

As described above, to build the Huffman tree, you will need to use a greedy approach that involves extracting the two Nodes with the lowest values in order to build a composite Node. To enable this greedy algorithm, you will be implementing a priority queue using a binary heap for this activity.

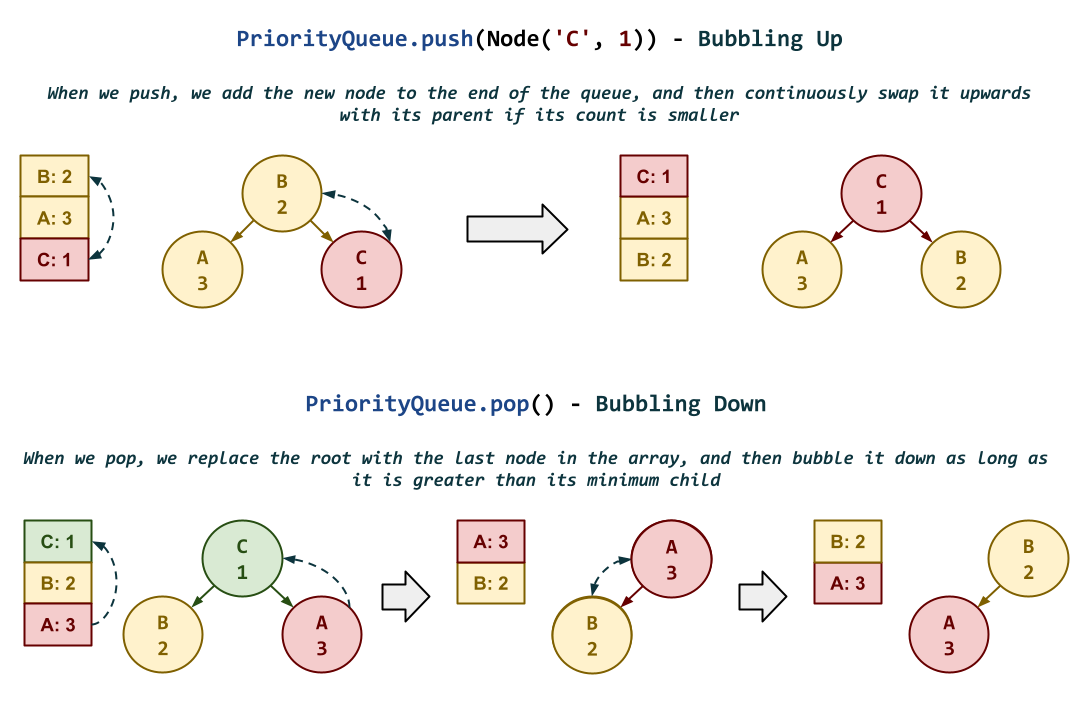
Although Python provides the heapq module, for this assignment, you are to implement your own binary heap, whose internal data representation is a list. You are not to use any functions from the heapq library.

Task 1: priority_queue.py¶

The priority_queue.py Python script contains the PriorityQueue class and utility functions you are to complete for this activity:

1. left_index(index: int) -> int:

   This function returns the index of the left child of the node specified by index.

2. right_index(index: int) -> int:

   This function returns the index of the right child of the node specified by index.

3. parent_index(index: int) -> int:

   This function returns the index of the parent of the node specified by index.

4. PriorityQueue.__len__(self) -> int:

   This method returns the number of values in the PriorityQueue.

5. PriorityQueue._bubble_up(self, index: int) -> None:

   This method performs the bubble up operation on the internal binary heap, beginning at the specified index:

   To maintain the binary heap invariant (ie. each node is never less than its children), continuously swap the current node with its parent if the current node is less than its parent*.

   Hints¶

   1. Consider doing this iteratively and think carefully about the ending condition.

   2. Remember that in Python, you can swap using destructured assignment:

      a, b = b, a
      

   3. The order of the comparisons matter. To have outputs consistent with the unit tests, you will want to do something like the following:

      if self.data[index] < self.data[parent]:
          # Perform swap
      

6. PriorityQueue.push(self, value) -> None:

   This method adds the value to the internal binary heap.

   Hint: Consider using PriorityQueue._bubble_up to maintain the binary heap invariant.

7. PriorityQueue._find_smallest_child(self, index: int) -> int:

   This method compares the children of the node specified by index and returns the index of the child with the smallest value.

   Hint: Be mindful of the bounds of the binary heap. Again, order is important, so when you compare the left and *right children, you want to do: self.data[left] < self.data[right].

8. PriorityQueue._bubble_down(self, index: int) -> None:

   This method performs the bubble down operation on the internal binary heap, beginning at the specified index:

   To maintain the binary heap invariant (ie. each node is never less than its children), continuously swap the current node with its parent if the current node is less than its parent*.

   Hints¶

   1. Consider doing this iteratively and think carefully about the ending condition.

   2. Remember that in Python, you can swap using destructured assignment:

      a, b = b, a
      

   3. The order of the comparisons matter. To have outputs consistent with the unit tests, you will want to do something like the following:

      if self.data[index] > self.data[smallest]:
          # Perform swap
      

9. PriorityQueue.pop(self):

   This method removes smallest value from the internal binary heap and returns it.

   Hint: After moving the last value in the binary heap to the root, consider using PriorityQueue._bubble_down to maintain the binary heap invariant.

Task 2: Testing¶

As you implement priority_queue.py, you can use the provided doctests to verify the correctness of your code:

# Run doctests
$ python3 -m doctest priority_queue.py -v
...
9 items passed all tests:
   2 tests in priority_queue.PriorityQueue.__len__
   3 tests in priority_queue.PriorityQueue._bubble_down
   3 tests in priority_queue.PriorityQueue._bubble_up
   2 tests in priority_queue.PriorityQueue._find_smallest_child
   3 tests in priority_queue.PriorityQueue.pop
   3 tests in priority_queue.PriorityQueue.push
   1 tests in priority_queue.left_index
   1 tests in priority_queue.parent_index
   1 tests in priority_queue.right_index
19 tests in 14 items.
19 passed and 0 failed.
Test passed.

You can also use make to run both the doctests and the unit tests:

# Run unit tests (and doctests)
$ make test-priority-queue
Testing priority queue ...
test_00_doctest (__main__.PriorityQueueTests) ... ok
test_01_mypy (__main__.PriorityQueueTests) ... ok
test_02_left_index (__main__.PriorityQueueTests) ... ok
test_03_right_index (__main__.PriorityQueueTests) ... ok
test_04_parent_index (__main__.PriorityQueueTests) ... ok
test_05_bubble_up (__main__.PriorityQueueTests) ... ok
test_06_push (__main__.PriorityQueueTests) ... ok
test_07_find_smallest_child (__main__.PriorityQueueTests) ... ok
test_08_bubble_down (__main__.PriorityQueueTests) ... ok
test_09_pop (__main__.PriorityQueueTests) ... ok
test_10_len (__main__.PriorityQueueTests) ... ok

   Score 4.00 / 4.00
  Status Success

----------------------------------------------------------------------
Ran 11 tests in 0.049s

OK

To just run the unit tests, you can do the following:

# Run unit tests
$ ./priority_queue_test.py -v
...

To run a specific unit test, you can specify the method name:

# Run only mypy unit test
$ ./priority_queue_test.py -v PriorityQueueTests.test_01_mypy
...

Activity 3: Huffman Coding (4 Points)¶

Once you have completed the Node and PriorityQueue classes, and have verified the walk function, you can now complete the Huffman coding script.

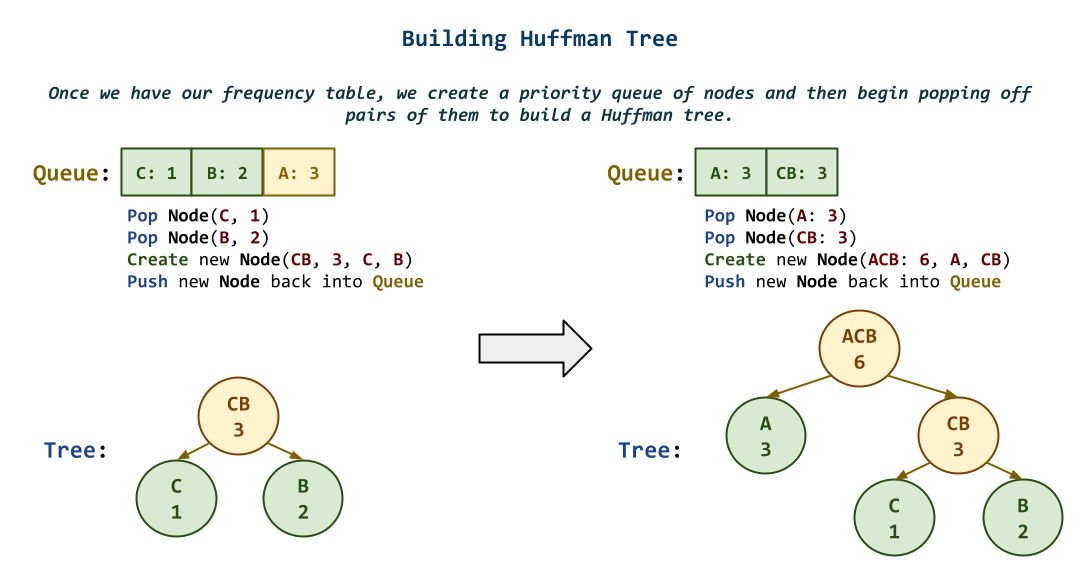
As described above, to build a Huffman tree, you will need to the following:

1. First, compute the frequencies of each symbol in the input stream.

2. Second, construct a priority queue of Nodes based on the frequency table computed in the previous step.

3. Third, use a greedy approach to build the Huffman tree by removing the two Nodes with the smallest value from the priority queue and then adding back to the priority queue a composite node.

4. Finally, walk the Huffman tree to determine the encoding for each symbol.

Task 1: huffman.py¶

For this task, you are to complete the huffman.py Python script by implementing the following functions:

1. count_frequencies(symbols: str) -> dict[str, int]

   This function returns a dict with the number of occurrences of each symbol in the symbols string.

   Hint: Consider using dict.get or collections.defaultdict.

2. compute_compression_ratio(symbols: str, codes: dict[str, str]) -> float

   This function returns the compression ratio if the input symbols string were encoded using the Huffman coding corresponding to the codes dict.

   Ratio = Number of Bits with Original Encoding / Number of Bits with Huffman Coding

   Hint: To determine the number of bits are required with the original encoding, you can ask Python to tell you the number of bytes for each symbol:

   symbol_bytes = len(bytes(symbol.encode()))
   

   Remember that each byte is 8 bits.

3. main(stream=sys.stdin) -> None:

   This function creates the Huffman coding of all the symbols in the input stream using the process described above.

   Hints¶

   1. To read all of a stream into a single string, you can use the read method.

   2. Consider using dict.items to loop over the frequency counts and push Node objects into your PriorityQueue.

   3. After building the Huffman tree using the while loop described above, you will need to walk the root to construct the Huffman codes.

   4. Print out each symbol and its corresponding Huffman code after sorting it by the length of the Huffman code and then the Huffman code itself.

      Remember that sorted takes a key argument that can be used to specified the priorities of an object for comparison.

   5. You can format floating point numbers with the following:

      f'{number:.2f}' # Use two decimal places
      

   6. Since some of the symbols may be escape characters, you can use the following to print out each symbol:

      f'{repr(symbol)[1:-1]}' # Use representation of symbol, strip quotes
      

Task 2: Testing¶

As you implement huffman.py, you can use the provided doctests to verify the correctness of your code:

# Run doctests
$ python3 -m doctest huffman.py -v
3 items passed all tests:
   2 tests in huffman.compute_compression_ratio
   1 tests in huffman.count_frequencies
   2 tests in huffman.main
5 tests in 4 items.
5 passed and 0 failed.

You can also use make to run both the doctests and the unit tests:

# Run unit tests (and doctests)
$ make test-huffman
test_00_doctest (__main__.HuffmanTests) ... ok
test_01_mypy (__main__.HuffmanTests) ... ok
test_02_count_frequencies (__main__.HuffmanTests) ... ok
test_03_compute_compression_ratio (__main__.HuffmanTests) ... ok
test_04_main (__main__.HuffmanTests) ... ok

   Score 4.00 / 4.00
  Status Success

----------------------------------------------------------------------
Ran 5 tests in 0.113s

OK

To just run the unit tests, you can do the following:

# Run unit tests
$ ./huffman_test.py -v
...

To run a specific unit test, you can specify the method name:

# Run only mypy unit test
$ ./huffman_test.py -v HuffmanTests.test_01_mypy
...

Activity 4: Quiz (2 Points)¶

Once you have completed all the activities above, you are to complete the following reflection quiz:

As with Reading 01, you will need to store your answers in a homework10/answers.json file. You can use the form above to generate the contents of this file, or you can write the JSON by hand.

To check your quiz directly, you can use the check.py script:

$ ../.scripts/check.py
Checking homework10 quiz ...
      Q1 0.20
      Q2 0.20
      Q3 1.00
      Q4 0.60
   Score 2.00 / 2.00
  Status Success

Leet Point (1 Extra Credit Point)¶

For extra credit, you are to solve the following LeetCode problem in Python.

2558. Take Gifts From the Richest Pile

To receive credit, you must pass on LeetCode and achieve an Accepted submission.

Submission¶

To submit your assignment, please commit your work to the homework10 folder of your homework10 branch in your assignments GitHub repository:

#-----------------------------------------------------------------------
# Make sure you have already completed Activity 0: Preparation
#-----------------------------------------------------------------------
...
$ git add node.py                             # Mark changes for commit
$ git commit -m "Homework 10: Activity 1"     # Record changes
...
$ git add priority_queue.py                   # Mark changes for commit
$ git commit -m "Homework 10: Activity 2"     # Record changes
...
$ git add huffman.py                          # Mark changes for commit
$ git commit -m "Homework 10: Activity 3"     # Record changes
...
$ git add answers.json                        # Mark changes for commit
$ git commit -m "Homework 10: Activity 4"     # Record changes
...

$ git push -u origin homework10               # Push branch to GitHub