CheckList 01

Overview

The midterm will cover the following topics:

Unit 1: Fundamental Data Structures
- Complexity
- C++
- Dynamic Arrays
- Linked Lists
- Stacks
- Queues
Unit 2: Sorting and Priority Queues
Unit 3: Searching and Search Trees

The midterm will consist of short answer and long answer questions.

Below are examples of the type of questions that may be asked on the midterm (many of them come from the exam last year). It is meant to be representative, rather than exhaustive (ie. there may be questions that show up on the midterm that are not shown below).

Short Answers

What is the worst-case time and space complexity of the following algorithm? Express your answers using Big-O notation in terms of len1 and len2.

using namespace std;

int edit_distance(const string &s1, const string &s2)
{
    const int len1 = s1.size(), len2 = s2.size();
    vector<vector<int>> d(len1+1);

    for (int i=0; i<=len1; ++i)
        d[i] = vector<int>(len2+1);

    d[0][0] = 0;
    for (int i = 1; i <= len1; ++i) d[i][0] = i;
    for (int i = 1; i <= len2; ++i) d[0][i] = i;

    for (int i = 1; i <= len1; ++i) {
        for (int j = 1; j <= len2; ++j) {
            d[i][j] = min(d[i-1][j], d[i][j-1]) + 1;
            if (s1[i-1] == s2[j-1])
                d[i][j] = min(d[i][j], d[i-1][j-1]);
            else
                d[i][j] = min(d[i][j], d[i-1][j-1] + 1);
        }
    }
    return d[len1][len2];
}

Time complexity:

Space complexity:

Which of the following data structures provide efficient (that is O(log(n)) or better) insertion?

unsorted array      sorted array        linked list         max binary heap     red-black tree      treap

Here is a step by step trace of a sorting algorithm. Which one? Briefly explain how you can tell by identifying the underlying data structure used to implement the algorithm.

Original: 7, 1, 5, 6, 8, 3
Pass 1:   1, 7, 5, 6, 8, 3
Pass 2:   1, 5, 7, 6, 8, 3
Pass 3:   1, 5, 6, 7, 8, 3
Pass 4:   1, 5, 6, 7, 8, 3
Pass 5:   1, 3, 5, 6, 7, 8

Consider the following sequence of push and pop operations.
```
c.clear();
c.push(5);
c.push(3);
c.pop();
c.push(2);
```
If c is of type stack<int>, what does c look like after the above operations?
```
Top     [   ]
        [   ]
         ...
        [   ]
Bottom  [   ]
```
If c is of type queue<int>, what does c look like after the above operations?
```
Front [   ][   ]...[   ][   ]  Back
```
For each of the following trees, identify if it is a max binary heap, a binary search tree, or both:

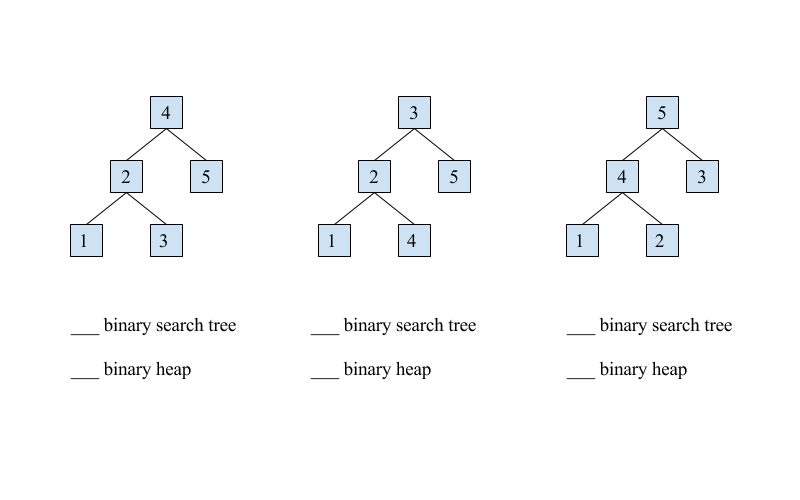
Long Answers

How would you implement a linked list in C++, including the following methods?
- Constructor
- Destructor
- Copy Constructor
- operator=
- push_front(T &value)
- operator[size_t index]
How would you implement a dynamic array in C++, including the following methods?
- Constructor
- Destructor
- Copy Constructor
- operator=
- push_back(T &value)
- operator[size_t index]
How would you implement Merge Sort on a linked list in C++?
How would you implement Quick Sort on a linked list in C++?
What would a B-Tree of order 4 (in which each node has 1-3 values and 2-4 children) look like after inserting the following letters (in the order shown): A, V, I, L, A. Show each step in order to get partial credit.

What would a Red-Black tree look like after inserting the same letters in the same order? Show each step in order to get partial credit. If you don't have red and black pens, clearly indicate what symbol means "black node" and what symbol means "red node."
You are building a contacts organizer for your phone. It needs to:
- Display the list of contacts alphabetically by first name or last name
- Search for a contact by first name or last name
- Display information (phone number, e-mail address) for a contact
- Add or remove contacts
Describe what data structures you would use to represent the contacts database, and what algorithms you would use to implement the above operations. You only need to identify the data structures and algorithms; you don't need to provide details about their implementation.