Challenge 17: A-Mazing Paths

In addition to playing board games with his children, the instructor has also introduced them to the joy of solving mazes. This activity helps keep the children occuppied when the family is at a restaurant or on a long road trip.

Of course, the children have grown tired of this obvious ploy to occupy their time and want you to help them find the shortest path through a maze starting from a single position to any number of end positions.

To make things easier for you, they have taken mazes and encoded them in the format shown below:

Each cell in the maze can be one of the following values:

• S: This is the starting cell.

• E: This is an ending cell.

• 0: This is an open cell.

• 1: This is a closed cell.

You can move through an open cell, but not a closed cell. From any open cell, you can move horizontally, vertically, or diagonally to another open or ending cell. Moving horizontally or vertically has a cost of 1, while moving diagonally has a cost of 2.

Since their father is a cruel person and has given them many mazes of varying sizes, they will send you a series of mazes encoded in the format above. You are to use Dijkstra's Algorithm to compute the shortest path from the start point to any of the end points and output both the cost and the path itself.

Input¶

The input will be a series of mazes in the following format:

ROWS COLS
Cell0_0 Cell0_1...
Cell1_0 Cell1_1...
...

That is, you will first be given two numbers, ROWS and COLS, which correspond to the number of rows and columns in the maze. This is followed by the CELLS in the maze where each line represents a row and the cells in the row are separated by spaces. The number of ROWS and COLS will be between 2 and 50 (inclusive).

The input will be terminated by two values of 0 for ROWS and COLS.

Example Input¶

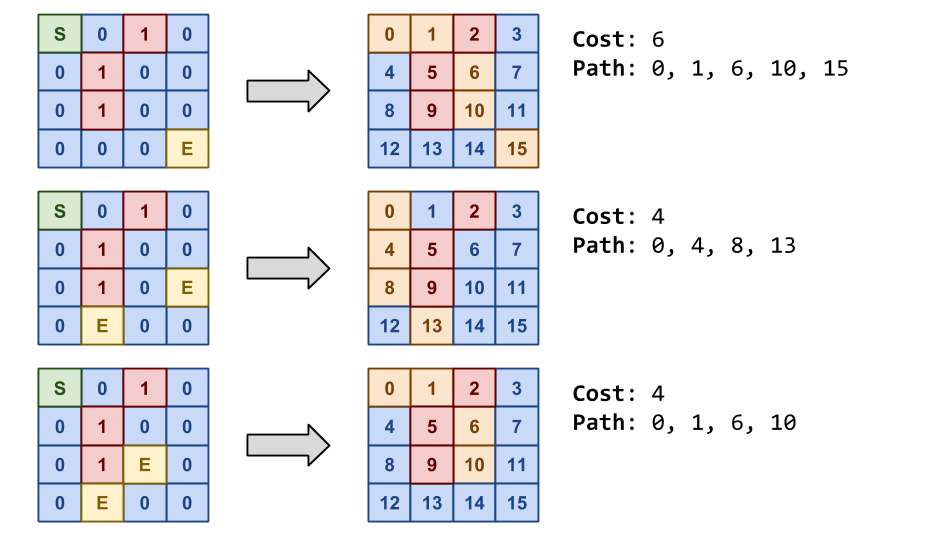
4 4
S 0 1 0
0 1 0 0
0 1 0 0
0 0 0 E
4 4
S 0 1 0
0 1 0 0
0 1 0 E
0 E 0 0
4 4
S 0 1 0
0 1 0 0
0 1 E 0
0 E 0 0
0 0

Output¶

For each test case, output the cost of the shortest path from the starting cell to any of the ending cells and the cells in the shortest path.

Example Output¶

Cost: 6 Path: 0 1 6 10 15
Cost: 4 Path: 0 4 8 13
Cost: 4 Path: 0 1 6 10

Note, as shown above, each cell is identified by a numerical ID based on its position in the maze:

Cell.Id = Cell.Row * Maze.Cols + Cell.Column

There should be spaces between each cell, but not after the last cell in the path.

If there are multiple paths with the same cost, choose the one where the path selects cells with lower numerical IDs from as shown in the third example.

If there are no possible paths from the starting cell to any of the ending cells, then output the following:

Cost: 0 Path: None

Submission¶

To submit your work, follow the same procedure you used for Reading 01:

$ cd path/to/cse-30872-su24-assignments     # Go to assignments repository
$ git checkout master                       # Make sure we are on master
$ git pull --rebase                         # Pull any changes from GitHub

$ git checkout -b challenge17               # Create and checkout challenge17 branch

$ $EDITOR challenge17/program.py            # Edit your code

$ git add challenge17/program.py            # Stage your changes
$ git commit -m "challenge17: done"         # Commit your changes

$ git push -u origin challenge17            # Send changes to GitHub

To check your code, you can use the .scripts/check.py script or curl:

$ .scripts/check.py
Checking challenge17 program.py ...
  Result Success
    Time 0.06
   Score 6.00 / 6.00

$ curl -F source=@challenge17/program.py https://dredd.h4x0r.space/code/cse-30872-su24/challenge17
{"result": "Success", "score": 6, "time": 0.06409883499145508, "value": 6, "status": 0}