Flow field facility

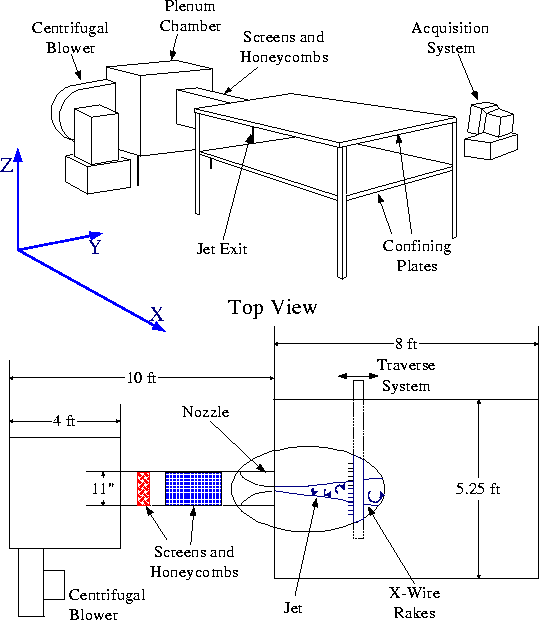
All the experiments were conducted in the planar jet facility located at the Hessert Center of the University of Notre Dame. A schematic of the facility is shown in Figure 1.

  

Figure 1: Schematic of the planar jet facility.

The facility is driven by a centrifugal blower. From the blower air discharges into a large settling chamber. From the chamber it passes through series of turbulence reducing screens and honeycombs. The jet is formed by a two-dimensional nozzle with a cubic polynomial contour with zero derivative end conditions. The nozzle is oriented in the vertical direction with aspect ratio height/width =36:1. The width of the slot is $D=0.5^{\prime \prime }$ . Through the nozzle the air discharges to the surrounding ambient environment. The flow is confined by two horizontal plates with separation of $18^{\prime \prime }$. The exit velocity is $U_o=35\ m/\sec$, with corresponding Re_D=28,000.The coordinate system is shown in Figure1 with x-axis starting at the origin of the jet in the streamwise direction, and y- and z-axis going in crosstream and spanwise direction correspondingly. In the crosstream direction the origin y=0 was taken at the centerline of the jet. The origin of the spanwise z-axis is chosen in the middle between the confining plates, with a positive direction upward.

A planar turbulent jet consists of three regions . The initial region of the jet consists of two planar shear layers with a core of irrotational flow in between. The shear layers widen and eventually are engulfed by $% x/D\approx 4$. After the shear layers merge, a complex interaction region is formed and extends to approximately $x/D\approx 10$, where the jet reaches a dynamical equilibrium and starts exhibiting a self-similar behavior of the mean profile. In other words, the mean flow at any streamwise station is self-similar when scaled by the local maximum velocity $U_{\max }$ and the local half-width b, the distance in crosstream direction between the centerline of the jet and the point where the U -component of velocity is equal to one half of $U_{\max }$.

The focus of this research is the self-similarity region and the measurement region spans the streamwise direction for x/D=50..90. The experimentally measured half-width b of the jet is presented in Figure 2.a) and follows the theoretical linear relationship b/D=k₁x/D+C₁, with $% k_1\approx 0.1$ in the measurement region.

  

Figure 2: a) Streamwise variation of the local half-width b/D and the local maximum velocity U_max, the crosstream variation of the normalized b) mean u-component and c) Reynolds stress $\overline{u'v'}$

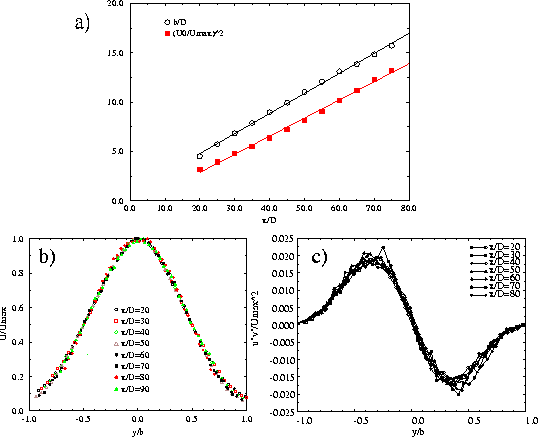The local maximum velocity also presented in Figure 2.a) and decays as follows, $(U_{\max }/U_0)^{-2}=k_2x/D+C_2$ with a value for $% k_2\approx 0.22$. Also normalized measurements of the mean u-component of the velocity, along with $\overline{u^{\prime }v^{\prime }}$ in crosstream direction are presented in the Figure and have revealed that all these quantities, as well as other second-order quantities (not shown) exhibit collapse into single profiles after $x/D\approx 50$. Thus, the self-similar region for second-order statistics starts approximately at this streamwise region. Measurements of mean characteristics of the jet show that the jet stays planar up to x/D=200 with a homogeneous spanwise z-direction.

Correlation measurements between the all three velocity components at several planes x/D=const are done by using of two rakes of x-wires with 8 evenly spaced probes each. See Figure 3 for the rake orientation.

  

Figure 3: Orientation of the rakes.

The usage of the rakes of the probes is motivated mainly by the fact that it dramatically speeds up the process of finding the cross-correlation tensor.

Both rakes are oriented in the cross-stream direction, parallel to each other. One rake is positioned on a manual traverse and another one is mounted on a computer-controlled traverse system. The traverse system allows one to control the location of the second rake with respect to the first one in the spanwise direction. Also both traverses move the rakes in the streamwise direction. Because the flow is homogeneous in spanwise direction and stationary, the cross-correlation matrix $R_{\alpha \beta }(y,y^{\prime },z,z^{\prime },t,t^{\prime })=\left\langle u_\alpha (y,z,t)u_\beta (y^{\prime },z^{\prime },t^{\prime })\right\rangle$ depends on $\Delta z=z-z^{\prime }$ and $\tau =t-t^{\prime }$ only. Here the velocity measurements $u_\alpha (y,z,t)$ corresponds to the first rake and $u_\beta (y^{\prime },z^{\prime },t^{\prime })$ corresponds to the second rake. Notations will be described in the following section. Probes on rakes are evenly spaced with $\Delta y=2^{\prime \prime }$. One rake is placed in the middle between the confining plates, which corresponds to K_z=0. The second rake is positioned below the first rake at 15 different equally spaced z-locations. From a preliminary measurement of the spanwise velocity correlation, the step in z-direction was chosen to be $% 0.75^{\prime \prime }$. At each z-location the velocities are sampled in blocks of 512 points for 500 blocks total with a non-dimensional sampling frequency of $St=f_sb/U_{\max }=2.0$. 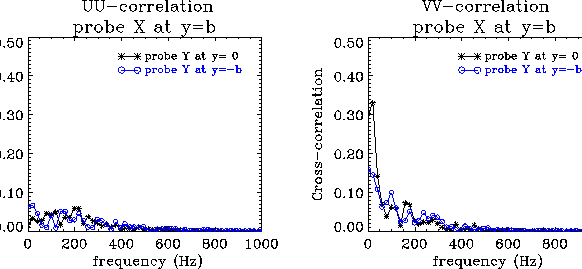For x/D=70, the dimensional sampling frequency is f_s=380 Hz. While for the conventional measurements in the turbulent flows this value of the sampling frequency is unacceptably low, the two-point cross-correlation measurements of Fourier transformed u-and v-components of the velocity for large-scale separations have shown essentially zero-level correlation above this frequency (see Figure 4).

  

Figure 4: Cross-correlation of the Fourier Transforms of u- and v-components, between three probes positioned at y=+b,0,-b at x/D=70.

The goal of this paper is to investigate large-scale coherent structures in the flow using the cross-correlation matrix measurements. From Figure 4 it can be seen that all energetically important structures lie in a low frequency region, so the usage of relatively low sampling rates was justified. Cut-off frequency of filters is chosen to be a half of the sampling frequency f_s to avoid temporal aliasing. Spatial aliasing was checked by doubling a number of probes at each rake and repeating the measurements. For the details see the results section.

Each x-wire is connected to an constant temperature anemometer with a low-pass filter. These circuits were built in-house. Voltages from transducers are read by an acquisition system consisting of MicroStar Laboratories simultaneous sample-and-hold boards. The system allows one to sample up to 512 channels simultaneously. For 32 channels the acquisition system gives a maximum sampling rate of 50 kHz/channel with no detectable phase lag between channels. Data are processed on a Gateway 2000 computer with Pentium Pro 200 processor. All the data primary processing codes are written in C language. The data were downloaded to a SPARC station 10 for further post-processing.

The x-wires are calibrated using a look-up table procedure.

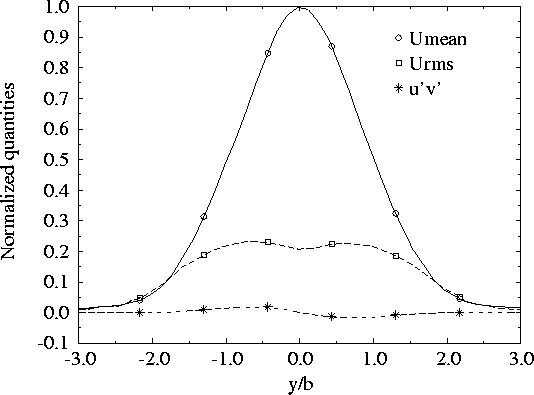
In order to check whether the rakes block the flow, a conventional measurements of the velocities were performed at x/D=70 and compared with a single x-probe measurements. The results are shown in Figure 5.

  

Figure 5: Comparisson between single X-probe (solid lines) and the rake of X-probes (symbols) measurements of the selected velocity quantities.

One can see that the blockage effect on the rake support system is negligible. So, the rakes don't disturb the jet and consequently the POD modes can be measured accurately.