Relevant Papers

A Paster & D Bolster
The effect of initial spatial correlations on late time kinetics of bimolecular irreversible reactions, Physica A, In Press

E Castro, D fernandez-Garcia, J Carrera and D Bolster
Visualization of mixing processes in a heterogeneous sand box aquifer, Environmental Science and Technology, 46 (6), pp 3228–3235

D Bolster and M Dentz
Anomalous Dispersion in Chemically Heterogeneous Media induced by Long Range Correlations, Journal of Fluid Mechanics, Volume 695, pp 366 - 389

A.M. Tartakovsky, P. de Anna, T Le Borgne, A Balter and D Bolster
Effect of spatial concentration fluctuations on effective kinetics in diffusion-reaction systems, Water Resources Research, 48, W02526, doi:10.1029/2011WR010720.

D. Bolster, P. de Anna, D.A. Benson and A.M. Tartakovsky
Incomplete Mixing and Reactions with Fractional Dispersion, Advances in Water Resources, 37 (2012) 86–93

Pietro de Anna, Tanguy Le Borgne, Marco Dentz, Diogo Bolster, and Philippe Davy
Anomalous Kinetics in Diffusion Limited Reactions Linked to Non-Gaussian Concentration PDF
Journal of Chemical Physics, 135, 174104 (2011); doi:10.1063/1.3655895

D Bolster, M Dentz and T Le Borgne
Hyper Mixing in Shear Flow Sites
Water Resources Research, Water Resour. Res., 47, W09602, doi:10.1029/2011WR010737

T Le Borgne, M Dentz, P, D Bolster, J Carrera, JR de Dreuzy and O Bour
Persistence of incomplete mixing: A key to anomalous transport
Physical Review E, 84, 015301(R)

D. Bolster, F.J. Valdes-Parada, T. Le Borgne, M. Dentz and J.Carrera
Mixing in Confined Stratified Aquifers
Journal of Contaminant Hydrology, doi: 10.1016/j.jconhyd.2010.02.003, Volumes 120-121, Pages 198-212

M Dentz, D Bolster
Distribution- versus correlation-induced anomalous transport in quenched random velocity fields
Physical Review Letters, 105, 244301

T Le Borgne, M Dentz, D Bolster, J Carrera, J-R de Dreuzy and P Davy
Non-Fickian mixing: temporal evolution of the scalar dissipation rate in porous media
Advances in Water Resources, doi:10.1016/j.advwatres.2010.08.006, Vol 33(12), P1468-1475

D Bolster, DA Benson, T LeBorgne and M Dentz
Anomalous mixing and reaction induced by superdiffusive nonlocal transport
Physical Review E, 82, 021119

Xavier Sanchez-Vila, Diogo Bolster
An Analytical Approach to Transient Homovalent Cation Exchange Problems
Journal of Hydrology, Volume 378, Issues 3-4, 30 November 2009, Pages 281-289

Donado LD, Sanchez-Vila X, Dentz M, Carrera J and Bolster D
'Multi-component reactive transport in multi-continuum media'
Water Resources Research, 45, W11402, doi:10.1029/2008WR006823

Bolster D, LeBorgne T and Dentz M (2009)
'Solute dispersion in channels with periodically varying apertures'
Physics of Fluids, 21, 056601

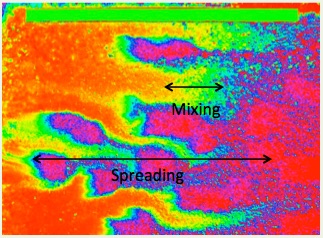
Mixing is a fundamental process that leads to the dilution of solutes and that brings different chemical species into contact with one another, and so driving biochemical reactions in fluids. Therefore, understanding and predicting mixing is a key step to predicting natural attenuation of solutes and reactive transport as it describes the rate at which reactants will meet. It is a field of study that has attracted the attention of researchers across a wide range of scientific communities, including those working in groundwater (and surface water) hydrology. In geophysical flows, mixing has applications in both porous media flows as well as in turbulent flows at various scales as found in river, limnological, oceanic and atmospheric flows . Heterogeneous velocity fields, which fluctuate at multiple scales, are typical in these applications and flow heterogeneities generate complex concentration distributions that enhance or indeed at times suppress mixing .

Historically much of the focus for transport in heterogeneous porous media has been on spreading, which at times was used as a metric of mixing (in fact the words have been used interchangeably. While there is a connection between the two, a fundamental difference exists between the concepts of spreading and mixing . Spreading describes the spatial extent of a solute plume and may typically be quantified in terms of (suitably defined) longitudinal spatial moments of the concentration distribution, while mixing can be seen as the process that increases the actual volume occupied by the solute; see figure below.